【深度优先搜索】和【广度优先搜索】的区别介绍-Toy模板网

这篇具有很好参考价值的文章主要介绍了【深度优先搜索】和【广度优先搜索】的区别介绍。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一. 前言

深度优先搜索（Depth-First Search，DFS）和广度优先搜索（Breadth-First Search，BFS）是两种常见的图搜索算法。它们的主要区别在于搜索的方式和顺序不同。

二. 区别

1. DFS的搜索方式是：

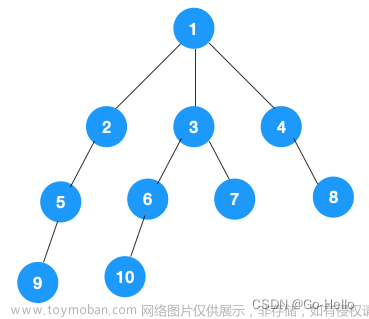
从某个节点出发，沿着一条路径直到底部，然后返回到前一个节点，继续搜索下一条路径，直到搜索完整张图。DFS使用栈或者递归来实现搜索过程。

具体步骤如下：

访问起始结点；
递归地访问第一个未被访问的相邻结点，如果没有未被访问的相邻结点，则回溯到上一个结点继续递归；
依次访问和递归每个未被访问的相邻结点，直到找到目标结点或到达叶子结点为止。

2. BFS的搜索方式是：

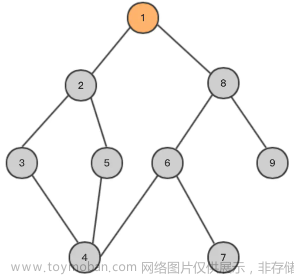
从某个节点出发，将其所有邻接节点加入到队列中，然后依次访问队列中的节点，将其邻接节点加入到队列中，以此类推，直到搜索完整张图。BFS使用队列来实现搜索过程。

具体步骤如下：

将起始结点放入队列中；
访问队列头部结点，将其未访问过的相邻结点加入队列尾部；
将队列头部结点出队列；
重复步骤 2 和 3，直到队列为空或找到目标结点。

三. 代码示例

1. 深度优先搜索代码示例：

示例一

def dfs(graph, start, target, path=[]):
    # 记录路径
    path = path + [start]
    # 到达目标结点，返回路径
    if start == target:
        return path
    # 遍历相邻结点
    for node in graph[start]:
        if node not in path:
            newpath = dfs(graph, node, target, path)
            if newpath:
                return newpath
    return None

示例二

class Graph:
    def __init__(self, graph_dict=None):
        if graph_dict is None:
            graph_dict = {}
        self.__graph_dict = graph_dict
 
    def add_vertex(self, vertex):
        if vertex not in self.__graph_dict:
            self.__graph_dict[vertex] = []
 
    def add_edge(self, edge):
        edge = set(edge)
        (vertex1, vertex2) = tuple(edge)
        if vertex1 in self.__graph_dict:
            self.__graph_dict[vertex1].append(vertex2)
        else:
            self.__graph_dict[vertex1] = [vertex2]
 
    def dfs(self, start, visited=None):
        if visited is None:
            visited = set()
        visited.add(start)
        print(start)
        for next in self.__graph_dict[start] - visited:
            self.dfs(next, visited)
        return visited
 
 
graph = {"A": {"B", "C"},
         "B": {"A", "D", "E"},
         "C": {"A", "F"},
         "D": {"B"},
         "E": {"B", "F"},
         "F": {"C", "E"}}
 
g = Graph(graph)
print("Depth First Search:")
g.dfs("A")

运行结果
【深度优先搜索】和【广度优先搜索】的区别介绍,python,数据结构-算法,深度优先,宽度优先,算法

2. 广度优先搜索代码示例：

示例一

from collections import deque

# 使用队列实现 BFS
def bfs(graph, start, target):
    # 使用 deque 实现双端队列
    queue = deque()
    queue.append(start)
    visited = set()
    visited.add(start)
    while queue:
        # 出队列
        node = queue.popleft()
        # 到达目标结点，返回
        if node == target:
            return True
        # 遍历相邻结点
        for neighbor in graph[node]:
            # 未访问过的结点入队列
            if neighbor not in visited:
                visited.add(neighbor)
                queue.append(neighbor)
    # 没有找到目标结点
    return False

示例二

from collections import deque
 
 
class Graph:
    def __init__(self, graph_dict=None):
        if graph_dict is None:
            graph_dict = {}
        self.__graph_dict = graph_dict
 
    def add_vertex(self, vertex):
        if vertex not in self.__graph_dict:
            self.__graph_dict[vertex] = []
 
    def add_edge(self, edge):
        edge = set(edge)
        (vertex1, vertex2) = tuple(edge)
        if vertex1 in self.__graph_dict:
            self.__graph_dict[vertex1].append(vertex2)
        else:
            self.__graph_dict[vertex1] = [vertex2]
 
    def bfs(self, start):
        visited, queue = set(), deque([start])
        visited.add(start)
        while queue:
            vertex = queue.popleft()
            print(vertex)
            for neighbour in self.__graph_dict[vertex]:
                if neighbour not in visited:
                    visited.add(neighbour)
                    queue.append(neighbour)
 
 
graph = {"A": {"B", "C"},
         "B": {"A", "D", "E"},
         "C": {"A", "F"},
         "D": {"B"},
         "E": {"B", "F"},
         "F": {"C", "E"}}
 
g = Graph(graph)
print("Breadth First Search:")
g.bfs("A")