面试算法53：二叉搜索树的下一个节点-Toy模板网

这篇具有很好参考价值的文章主要介绍了面试算法53：二叉搜索树的下一个节点。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

题目

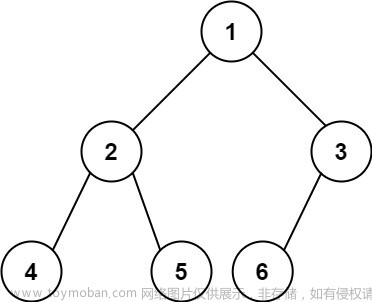
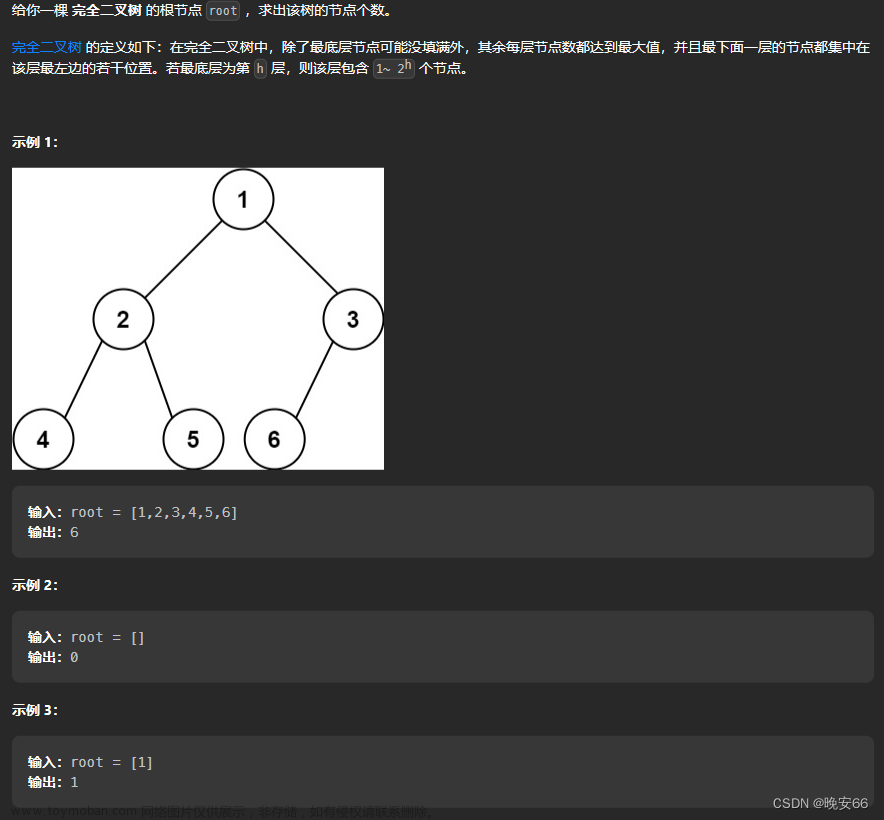
给定一棵二叉搜索树和它的一个节点p，请找出按中序遍历的顺序该节点p的下一个节点。假设二叉搜索树中节点的值都是唯一的。例如，在图8.9的二叉搜索树中，节点8的下一个节点是节点9，节点11的下一个节点是null。
面试算法53：二叉搜索树的下一个节点,算法,算法,面试,java

分析：时间复杂度O（n）的解法

解决这个问题的最直观的思路就是采用二叉树的中序遍历。可以用一个布尔变量found来记录已经遍历到节点p。该变量初始化为false，遍历到节点p就将它设为true。在这个变量变成true之后遍历到的第1个节点就是要找的节点。

解：时间复杂度O（n）的解法

public class Test {
    public static void main(String[] args) {
        TreeNode node1 = new TreeNode(1);
        TreeNode node2 = new TreeNode(2);
        TreeNode node3 = new TreeNode(3);
        TreeNode node4 = new TreeNode(4);
        TreeNode node5 = new TreeNode(5);
        TreeNode node6 = new TreeNode(6);

        node4.left = node2;
        node4.right = node5;
        node2.left = node1;
        node2.right = node3;
        node5.right = node6;

        TreeNode result = inorderSuccessor(node4, node5);
        System.out.println(result);
    }

    public static TreeNode inorderSuccessor(TreeNode root, TreeNode p) {
        Stack<TreeNode> stack = new Stack<>();

        TreeNode cur = root;
        boolean found = false;
        while (cur != null || !stack.isEmpty()) {
            while (cur != null) {
                stack.push(cur);
                cur = cur.left;
            }

            cur = stack.pop();
            if (found) {
                break;
            }
            else if (p == cur) {
                found = true;
            }

            cur = cur.right;
        }

        return cur;
    }
}

分析：时间复杂度O（h）的解法

下面按照在二叉搜索树中根据节点的值查找节点的思路来分析。从根节点开始，每到达一个节点就比较根节点的值和节点p的值。如果当前节点的值小于或等于节点p的值，那么节点p的下一个节点应该在它的右子树。如果当前节点的值大于节点p的值，那么当前节点有可能是它的下一个节点。此时当前节点的值比节点p的值大，但节点p的下一个节点是所有比它大的节点中值最小的一个，因此接下来前往当前节点的左子树，确定是否能找到值更小但仍然大于节点p的值的节点。重复这样的比较，直至找到最后一个大于节点p的值的节点，就是节点p的下一个节点。文章来源地址https://www.toymoban.com/news/detail-741755.html

解：时间复杂度O（h）的解法

public class Test {
    public static void main(String[] args) {
        TreeNode node1 = new TreeNode(1);
        TreeNode node2 = new TreeNode(2);
        TreeNode node3 = new TreeNode(3);
        TreeNode node4 = new TreeNode(4);
        TreeNode node5 = new TreeNode(5);
        TreeNode node6 = new TreeNode(6);

        node4.left = node2;
        node4.right = node5;
        node2.left = node1;
        node2.right = node3;
        node5.right = node6;

        TreeNode result = inorderSuccessor(node4, node5);
        System.out.println(result);
    }

    public static TreeNode inorderSuccessor(TreeNode root, TreeNode p) {
        TreeNode cur = root;
        TreeNode result = null;
        while (cur != null) {
            if (cur.val > p.val) {
                result = cur;
                cur = cur.left;
            }
            else {
                cur = cur.right;
            }
        }

        return result;
    }
}