1 TSP数学模型

2 callback消除子环路(subtour)
- callback解决方案
The constraints (3) exclude subtours by imposing that for any proper subset S of the vertex set V such that |S| ≥ 2 a solution cannot encompass a cycle within S. However, as there is an exponential number of subsets of V , it is impractical to specify all of these constraints. A possible approach is to iteratively solve the problem, starting without these constraints and after each solving round add constraints (3) violated by the current solution.
- SCIP中的callback方式
一般商业求解器Gurobi或者CPLEX中直接提供的callback(回调函数)的方法,SCIP采用的是constraint handler的方式,使用起来没那么方便,需要自定义一个继承了约束处理的类Conshdlr,覆写conscheck、consenfolp、conslock方法。看源码其实就是callback的一种实现形式而已,其运行日志显示也是迭代运行求解的。文章来源:https://www.toymoban.com/news/detail-741906.html
3 python调用SCIP求解TSP
- 完整python代码如下:
import numpy as np
import networkx as nx
import itertools
from pyscipopt import Model, Conshdlr, quicksum, SCIP_RESULT
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] # 替换sans-serif字体
plt.rcParams['axes.unicode_minus'] = False # 正常显示负号
# 继承约束处理的类
class TSPconshdlr(Conshdlr):
def __init__(self, variables):
self.variables = variables
def find_subtours(self, solution = None):
# find subtours in the graph induced by the edges {i,j} for which x[i,j] is positive
# at the given solution; when solution is None, then the LP solution is used
# 获取所有连接边
edges = []
x = self.variables
for (i, j) in x:
if self.model.getSolVal(solution, x[i, j]) > 1.e-6:
edges.append((i, j))
# 判断图是否有连接,如果返回的长度=1,则说明没有子连接
G = nx.Graph()
G.add_edges_from(edges)
components = list(nx.connected_components(G))
if len(components) == 1:
return []
else:
return components
# checks whether solution is feasible, ie, if there are no subtours;
# since the checkpriority is < 0, we are only called if the integrality
# constraint handler didn't find infeasibility, so solution is integral
def conscheck(self, constraints, solution, check_integrality,
check_lp_rows, print_reason, completely, **results):
""" calls feasibility check method of constraint handler """
if self.find_subtours(solution):
return {"result": SCIP_RESULT.INFEASIBLE}
else:
return {"result": SCIP_RESULT.FEASIBLE}
def consenfolp(self, constraints, n_useful_conss, sol_infeasible):
""" calls enforcing method of constraint handler for LP solution for all constraints added """
subtours = self.find_subtours()
if subtours:
x = self.variables
# 添加子环消除路约束
for subset in subtours:
self.model.addCons(quicksum(x[i, j] for(i, j) in pairs(sorted(subset))) <= len(subset) - 1)
print("cut: len(%s) <= %s" % (subset, len(subset) - 1))
return {"result": SCIP_RESULT.CONSADDED}
else:
return {"result": SCIP_RESULT.FEASIBLE}
def conslock(self, constraint, locktype, nlockspos, nlocksneg):
# 可以直接跳过
pass
# def conslock(self, constraint, locktype, nlockspos, nlocksneg):
# x = self.variables
# for (i,j) in x:
# self.model.addVarLocks(x[i,j], nlocksneg, nlockspos)
def pairs(nodes):
return itertools.combinations(nodes, 2)
def get_route_data(edges):
# 解析获取路径,构成一个环
routes = []
for i in range(len(edges)):
if i == 0:
routes.append(edges[0])
edges.pop(0)
else:
pre = routes[-1]
connected_node = pre[1]
for j in range(len(edges)):
aft = edges[j]
if connected_node in aft:
if aft[0] == connected_node:
chosen_node = (aft[0], aft[1])
elif aft[1] == connected_node:
chosen_node = (aft[1], aft[0])
routes.append(chosen_node)
edges.pop(j)
break
i = i+1
return routes
def plot_pic(route, city_location):
plt.figure()
# 绘制散点
x = np.array(city_location)[:, 0] # 横坐标
y = np.array(city_location)[:, 1] # 纵坐标
plt.scatter(x, y, color='r')
# 绘制城市编号
for i, txt in enumerate(range(1, len(city_location) + 1)):
plt.annotate(txt, (x[i], y[i]))
# 绘制方向
x0 = x[route]
y0 = y[route]
for i in range(len(city_location) - 1):
plt.quiver(x0[i], y0[i], x0[i + 1] - x0[i], y0[i + 1] - y0[i], color='b', width=0.005, angles='xy', scale=1,
scale_units='xy')
plt.quiver(x0[-1], y0[-1], x0[0] - x0[-1], y0[0] - y0[-1], color='b', width=0.005, angles='xy', scale=1,
scale_units='xy')
plt.title('TSP')
plt.xlabel('x')
plt.ylabel('y')
plt.savefig('./TSP.png')
plt.show()
def pre_test_data():
# 城市节点的位置信息,一行代表一个城市的横坐标及纵坐标
city_location = [[ 94, 99],
[ 66, 67],
[ 14, 78],
[ 95, 56],
[ 68, 9],
[ 26, 20],
[ 51, 67],
[ 39, 39],
[ 5, 55],
[ 12, 33],
[ 55, 85],
[ 98, 46],
[ 36, 39],
[ 65, 100],
[ 57, 89],
[ 88, 24],
[ 53, 96],
[ 91, 41],
[ 32, 69],
[ 38, 38],
[ 38, 39],
[ 85, 100],
[ 7, 37],
[ 85, 96],
[ 89, 48],
[ 85, 35],
[ 32, 29],
[ 31, 25],
[ 20, 17],
[ 75, 21],
[ 74, 29],
[ 6, 32],
[ 20, 81],
[ 62, 1],
[ 11, 48],
[ 1, 69],
[ 99, 70],
[ 20, 27],
[ 25, 42],
[ 6, 31],
[ 78, 24],
[ 42, 39],
[ 83, 30],
[ 94, 10],
[ 90, 37],
[ 76, 73],
[ 9, 56],
[ 39, 33],
[ 74, 15],
[ 77, 14]]
nodes = list(range(len(city_location))) # 节点集合
# 计算距离成本矩阵 distance, 直接使用欧式距离
distance = {}
for (i, j) in pairs(nodes):
distance[(i, j)] = ((city_location[i][0]-city_location[j][0])**2+(city_location[i][1]-city_location[j][1])**2)**0.5
return nodes, city_location, distance
def solve_tsp(nodes, distance):
# 构建模型
model = Model("TSP")
# 定义变量: 为了减少决策变量,节点i和j是否连接(无方向),即(1,2)代表1和2连接,不代表1->2
x = {}
for (i, j) in pairs(nodes):
x[i, j] = model.addVar(vtype="B", name="x(%s,%s)" % (i, j))
# 添加流约束
for i in nodes:
model.addCons(quicksum(x[j, i] for j in nodes if j < i) +
quicksum(x[i, j] for j in nodes if j > i) == 2, "Degree(%s)" % i)
# 去除子环路
conshdlr = TSPconshdlr(x)
model.includeConshdlr(conshdlr, "TSP", "TSP subtour eliminator", chckpriority=-10, needscons=False)
model.setBoolParam("misc/allowstrongdualreds", False)
# 设置目标
model.setObjective(quicksum(distance[i, j] * x[i, j] for (i, j) in pairs(nodes)), "minimize")
# 求解
model.hideOutput()
model.optimize()
# 获取结果
if model.getStatus() != 'infeasible':
edges = []
for (i, j) in x:
if model.getVal(x[i, j]) > 1.e-6:
edges.append((i, j))
routes = get_route_data(edges)
print("Optimal routes:", routes)
print("Optimal cost:", model.getObjVal())
else:
print('model is infeasible')
return routes
if __name__ == "__main__":
############## 准备测试数据 ##############
nodes, city_location, distance = pre_test_data()
############## 建模 & 求解 ##############
route = solve_tsp(nodes, distance)
############## 绘图结果 ##############
plot_pic(route, city_location)
4 求解结果
4.1 log日志
cut: len({0, 21, 23}) <= 2
cut: len({1, 2, 3, 4, 6, 7, 8, 11, 12, 15, 17, 18, 19, 20, 24, 25, 26, 27, 32, 33, 34, 35, 36, 38, 41, 42, 43, 44, 45, 46, 47, 48, 49}) <= 32
cut: len({37, 28, 5}) <= 2
cut: len({9, 31, 22, 39}) <= 3
cut: len({16, 10, 13, 14}) <= 3
cut: len({40, 29, 30}) <= 2
cut: len({0, 1, 36, 6, 10, 45, 13, 14, 16, 21, 23}) <= 10
cut: len({32, 2, 18}) <= 2
cut: len({24, 11, 3}) <= 2
cut: len({48, 33, 4}) <= 2
cut: len({34, 37, 5, 39, 7, 9, 41, 38, 12, 47, 19, 20, 22, 26, 27, 28, 31}) <= 16
cut: len({8, 35, 46}) <= 2
cut: len({40, 42, 43, 15, 49, 29, 30}) <= 6
cut: len({17, 44, 25}) <= 2
cut: len({0, 13, 21, 23}) <= 3
cut: len({1, 2, 3, 4, 5, 6, 8, 9, 11, 15, 17, 18, 24, 25, 26, 27, 28, 29, 30, 32, 33, 34, 35, 36, 37, 38, 40, 42, 43, 44, 45, 46, 47, 48, 49}) <= 34
cut: len({7, 41, 12, 19, 20}) <= 4
cut: len({16, 10, 14}) <= 2
cut: len({31, 22, 39}) <= 2
cut: len({0, 1, 36, 6, 10, 45, 13, 14, 16, 18, 21, 23}) <= 11
cut: len({32, 2, 35}) <= 2
cut: len({24, 11, 3, 17}) <= 3
cut: len({33, 4, 40, 42, 43, 44, 15, 48, 49, 25, 29, 30}) <= 11
cut: len({37, 5, 39, 7, 9, 41, 38, 12, 47, 19, 20, 22, 26, 27, 28, 31}) <= 15
cut: len({8, 34, 46}) <= 2
cut: len({0, 10, 13, 14, 16, 21, 23}) <= 6
cut: len({1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 15, 17, 18, 19, 20, 22, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49}) <= 42
cut: len({0, 1, 36, 10, 45, 13, 14, 16, 21, 23}) <= 9
cut: len({2, 5, 6, 7, 8, 9, 12, 18, 19, 20, 22, 26, 27, 28, 31, 32, 34, 35, 37, 38, 39, 41, 46, 47}) <= 23
cut: len({3, 11, 44, 17, 24}) <= 4
cut: len({33, 4, 40, 42, 43, 15, 48, 49, 25, 29, 30}) <= 10
cut: len({0, 1, 6, 10, 13, 45, 14, 16, 21, 23}) <= 9
cut: len({2, 5, 7, 8, 9, 12, 18, 19, 20, 22, 26, 27, 28, 31, 32, 34, 35, 37, 38, 39, 41, 46, 47}) <= 22
cut: len({11, 3, 36}) <= 2
cut: len({33, 4, 40, 42, 43, 15, 48, 49, 29, 30}) <= 9
cut: len({24, 17, 44, 25}) <= 3
Optimal routes: [(0, 21), (21, 23), (23, 13), (13, 16), (16, 14), (14, 10), (10, 45), (45, 1), (1, 6), (6, 18), (18, 32), (32, 2), (2, 35), (35, 8), (8, 46), (46, 34), (34, 22), (22, 31), (31, 39), (39, 9), (9, 37), (37, 28), (28, 5), (5, 27), (27, 26), (26, 38), (38, 12), (12, 19), (19, 20), (20, 7), (7, 41), (41, 47), (47, 33), (33, 4), (4, 48), (48, 49), (49, 43), (43, 15), (15, 40), (40, 29), (29, 30), (30, 42), (42, 25), (25, 44), (44, 17), (17, 24), (24, 11), (11, 3), (3, 36), (36, 0)]
Optimal cost: 508.0830635384923
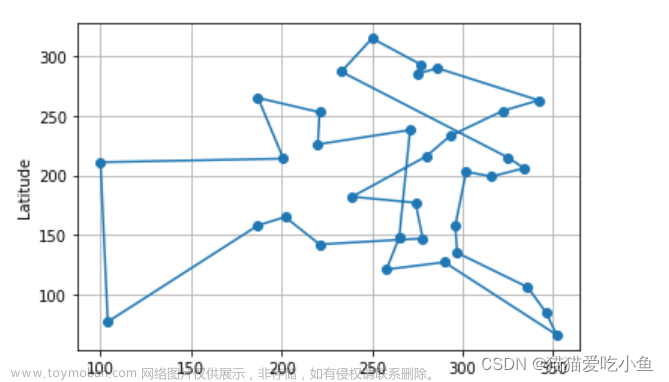
4.2 绘图结果

参考:PySCIPOPT接口文档文章来源地址https://www.toymoban.com/news/detail-741906.html
到了这里,关于python调用SCIP求解TSP(callback方式实现消除子环路subtour)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!