verilog实现二进制转BCD码-加3移位法-Toy模板网

这篇具有很好参考价值的文章主要介绍了verilog实现二进制转BCD码-加3移位法。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

简介

BCD码用4位二进制数表示一个十进制数，最常用的BCD码是8421码，用4’b0000-4’b1001表示十进制数字0-9，接下来默认BCD码就是8421码。

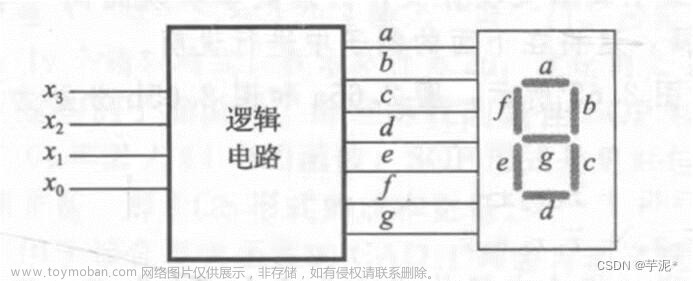
在FPGA中使用数码管时，段选信号不好记，所以我们用BCD码表示一个数码管的数值，将BCD码转化为段选信号驱动数码管，数码管驱动可以这篇文章：74hc595驱动数码管。例如，当我们想要6个数码管显示123456时，只需要给数码管驱动模块传入{4’h1, 4’h2, 4’h3, 4’h4, 4’h5, 4’h6}即可。

但这样做依然不够方便，例如，当我们采集到某个10bit二进制数时，想要将其显示在数码管上，该怎么办？此时就需要进行二进制转BCD码的操作，最简单粗暴的方法为使用除法，但fpga中使用除法消耗资源过多，因此通常用加三移位法。

加三移位法

4位二进制数取值范围为0-15，为16进制，而BCD码为0-9，为10进制，如果4位二进制数逢十进一，就能得到BCD码，所以需要对大于9的4位二进制数进行+6强制进位

加三移位法即上述方法的改进，占用更少的资源。由于4位二进制数大于9时需要+6调整，那么其大于4时，其左移后会大于9，所以左移前进行+3调整，等同于左移后+6。

对于大于4位的二进制数，通过左移，每4位大于4的都+3调整，可将任意位的二进制数转化为BCD码。
注意：最后一次左移后不需要调整，因为不再会左移，任意4位大于4也没关系

参考网上的例子，以8bit二进制数8’hff为例：

0           1111 1111;          //原数
1           0000 0001;          //左移一次
2           0000 0011;          //左移二次
3           0000 0111;          //左移三次,检查低四位>4?
3.1.        0000 1010;          //大于4，加3进行调整
4           0001 0101;          //左移四次,检查低四位>4?
4.1.        0001 1000;          //大于4，加3进行调整
5           0011 0001;          //左移五次
6           0110 0011;          //左移六次,检查高四位>4?
6.1.        1001 0011;          //大于4，加3进行调整
7           1 0010 0111;         //左移七次,检查低四位>4?
7.1.        1 0010 1010;         //大于4，加3进行调整
8           10 0101 0101;        //左移八次(得到BCD码255)

更多细节可以看这篇文章：走近FPGA之二进制转BCD码

RTL代码与仿真

给大于4就+3这个操作编写一个模块Adder：

module Adder(
    input [3:0] i_data,
    output [3:0] o_data
);
    assign o_data = (i_data > 4'h4) ? (i_data + 4'h3) : i_data;
endmodule

以10bit二进制数转BCD码为例，其RTL图如下所示：
加三移位法,FPGA,数码管,fpga开发

首先，0和A9，A8，A7构成了左移3次后的低4位，Adder1对其进行+3调整，输出o1，o1低3位与A6构成了左移4次的低4位，同理Adder2的输出o2的低3位与A5构成了左移5次的低四位，后续Adder3~Adder7同理。第一层到第七层分别为左移3次到左移9次的调整，其它Adder的作用可以参考上述8位二进制数转BCD码的流程。

根据上图，可以轻易写出10位二进制转BCD码的RTL代码：

module bin2bcd_10bit(
    input   [9:0]   i_data,
    output  [15:0]  o_bcd
);
//------------signals--------------
wire [3:0] o1, o2, o3, o4, o5, o6, o7, o8, o9, o10, o11, o12;
//------------function-------------
Adder Adder1 (
    .i_data ({1'b0, i_data[9:7]}), 
    .o_data (o1)
);
Adder Adder2 (
    .i_data ({o1[2:0], i_data[6]}), 
    .o_data (o2)
);
Adder Adder3 (
    .i_data ({o2[2:0], i_data[5]}), 
    .o_data (o3)
);
Adder Adder4 (
    .i_data ({o3[2:0], i_data[4]}), 
    .o_data (o4)
);
Adder Adder5 (
    .i_data ({o4[2:0], i_data[3]}), 
    .o_data (o5)
);
Adder Adder6 (
    .i_data ({o5[2:0], i_data[2]}), 
    .o_data (o6)
);
Adder Adder7 (
    .i_data ({o6[2:0], i_data[1]}), 
    .o_data (o7)
);
Adder Adder8 (
    .i_data ({1'b0, o1[3], o2[3], o3[3]}), 
    .o_data (o8)
);
Adder Adder9 (
    .i_data ({o8[2:0], o4[3]}), 
    .o_data (o9)
);
Adder Adder10 (
    .i_data ({o9[2:0], o5[3]}), 
    .o_data (o10)
);
Adder Adder11 (
    .i_data ({o10[2:0], o6[3]}), 
    .o_data (o11)
);
Adder Adder12 (
    .i_data ({1'b0, o8[3], o9[3], o10[3]}), 
    .o_data (o12)
);
assign o_bcd = {3'b000, o12, o11, o7, i_data[0]};
endmodule

编写仿真tb，输入20个随机10位二进制数，输出bcd码的hex格式：

`timescale 1ps/1ps
`define CLK_CYCLE 20

module bin2bcd_8bit_tb;

//----------clk generate-----------
reg clk = 1'b1;
always #(`CLK_CYCLE/2) clk = ~clk;

//-----------signals---------------
reg rst_n = 1'b0;
reg [9:0] i_data = 10'd0;
wire [15:0] o_data;

//----------instantiation----------
bin2bcd_10bit inst_bin2bcd_10bit (
    .i_data (i_data), 
    .o_bcd  (o_data)
);

//-----------simulation------------
initial begin
    // reset first
    @(negedge clk) rst_n = 1'b1;
    @(posedge clk);
    
    $monitor("input(decimal): %d, output(hex): %h, time: %t", i_data, o_data, $time);
    repeat(20) begin
        i_data = $random;
        #(`CLK_CYCLE);
    end

    // stop/finish
    #(`CLK_CYCLE * 10) $finish;
end

endmodule

仿真结果如下：
加三移位法,FPGA,数码管,fpga开发
可以看出20次二进制数转BCD码都成功了，之后可以用该模块加上数码管译码模块直接进行10bit二进制数的数码管显示。

16bit二进制转bcd码也同理，其RTL图如下：
加三移位法,FPGA,数码管,fpga开发
可以看出组合逻辑非常多，有13层加三移位Adder，为了降低组合逻辑延时，可以进行流水线加速，这里就不具体展开了。文章来源地址https://www.toymoban.com/news/detail-742074.html