运筹系列82：使用动态规划求解TSP问题-Toy模板网

这篇具有很好参考价值的文章主要介绍了运筹系列82：使用动态规划求解TSP问题。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

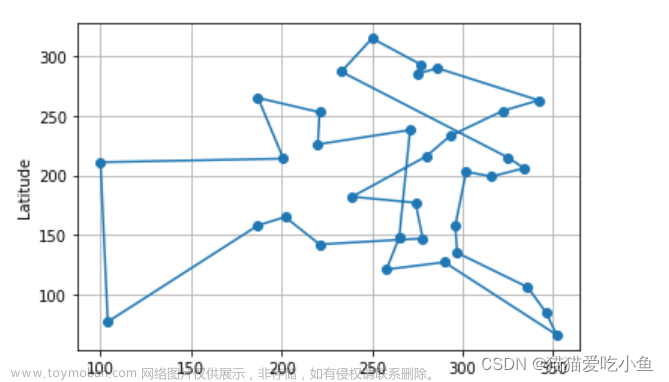
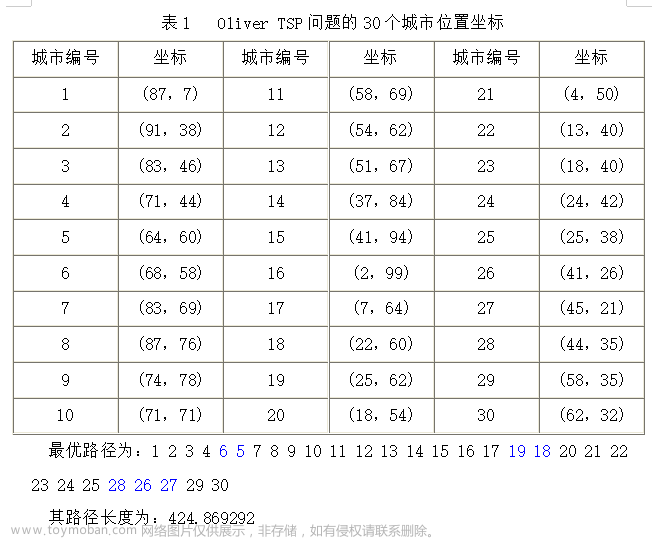
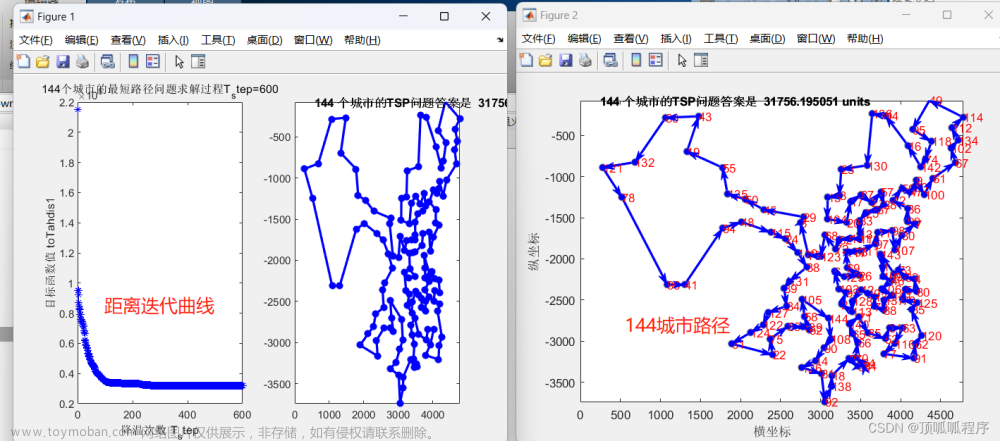
1. 动态规划思路和小技巧

定义 $c (s, k)$ 为当前在 $k$ ，待访问点的集合 $s$ ，最后返回城市0的最短路径，那么Bellman方程为：
$c(s,k)=\min_{i \in s}\{c(s-\{i\},i)+d_{i,k}\}$
为了使用方便，这里使用一个trick，即使用二进制来表达，用位运算符来计算，称作set bits：

左移和右移运算符可以快速计算2的幂：每左移一位，相当于该数乘以2；每右移一位，相当于该数除以2。因此，1 << k等价于 $2^k$ 。假设S中包含 $k_1,...,k_n$ ，则我们可以将s等价替换位 $S=2^{k_1}+...+2^{k_n}$
按位或运算符|：可以用来计算集合的并集
按位与运算符&和取反运算符 ~：可以用来计算集合的差集

我们有初始状态 $c(\{0\},k)=(d_{0,k},0)$ 。
逐步扩大set的尺寸，遍历所有可能的subset，使用bellman方程迭代计算。我们以n=5为例进行计算，初始状态为：
tsp 动态规划,运筹学,动态规划,算法,机器学习

第一轮结束后，状态清单为：
tsp 动态规划,运筹学,动态规划,算法,机器学习

第三轮结束后，状态清单为：

tsp 动态规划,运筹学,动态规划,算法,机器学习

第四轮结束后，状态清单为：
tsp 动态规划,运筹学,动态规划,算法,机器学习

2. Julia代码示例

using Combinatorics
function held_karp(dists::Array{Int64, 2})
    n = size(dists,1)
    C = Dict{Tuple{Int64, Int64},Tuple{Int64, Int64}}()
    for k in 1:n-1
        C[(1 << k, k)] = (dists[n,k], n)
    end
    for subset_size in 2:n-1
        for subset in combinations(1:n-1,subset_size)
            bits = 0
            for bit in subset;bits |= 1 << bit;end
            for k in subset
                prev = bits & ~(1 << k)
                res =  Array{Tuple{Int64, Int64},1}()
                for m in subset
                    if m == k;continue;end
                    push!(res,(C[(prev,m)][1]+dists[m,k],m))
                end
                C[(bits,k)] = minimum(res)
            end        
        end
    end
    bits = 1<<n - 2
    res = Array{Tuple{Int64, Int64},1}()
    for k in 1:n-1
        push!(res, (C[(bits, k)][1] + dists[k,n], k))
    end
    opt, parent = minimum(res)
    path = []
    for i in 1:n-1
        push!(path,parent)
        new_bits = bits & ~(1 << parent)
        _, parent = C[(bits, parent)]
        bits = new_bits
    end
    path
end

3. python代码示例

import itertools
import random
import sys

def generate_distances(n):
    dists = [[0] * n for i in range(n)]
    for i in range(n):
        for j in range(i+1, n):
            dists[i][j] = dists[j][i] = random.randint(1, 99)
    return dists
    
def held_karp(dists):
    """
    Implementation of Held-Karp, an algorithm that solves the Traveling
    Salesman Problem using dynamic programming with memoization.
    Parameters:
        dists: distance matrix
    Returns:
        A tuple, (cost, path).
    """
    n = len(dists)

    # Maps each subset of the nodes to the cost to reach that subset, as well
    # as what node it passed before reaching this subset.
    # Node subsets are represented as set bits.
    C = {}

    # Set transition cost from initial state
    for k in range(1, n):
        C[(1 << k, k)] = (dists[0][k], 0)

    # Iterate subsets of increasing length and store intermediate results
    # in classic dynamic programming manner
    for subset_size in range(2, n):
        for subset in itertools.combinations(range(1, n), subset_size):
            # Set bits for all nodes in this subset
            bits = 0
            for bit in subset:
                bits |= 1 << bit

            # Find the lowest cost to get to this subset
            for k in subset:
                prev = bits & ~(1 << k)

                res = []
                for m in subset:
                    if m == 0 or m == k: # 不允许回到0，不允许为当前点
                        continue
                    res.append((C[(prev, m)][0] + dists[m][k], m))
                C[(bits, k)] = min(res)

    # We're interested in all bits but the least significant (the start state)
    bits = (2**n - 1) - 1

    # Calculate optimal cost
    res = []
    for k in range(1, n):
        res.append((C[(bits, k)][0] + dists[k][0], k))
    opt, parent = min(res)

    # Backtrack to find full path
    path = []
    for i in range(n - 1):
        path.append(parent)
        new_bits = bits & ~(1 << parent)
        _, parent = C[(bits, parent)]
        bits = new_bits

    # Add implicit start state
    path.append(0)

    return opt, list(reversed(path))

def held_karp2(dists):
    n = len(dists)
    C = {}
    for k in range(1, n):
        C[(1, k)] = (dists[0][k], 0)
    for subset_size in range(1, n):
        for m in range(1, n):
            for subset in itertools.combinations(list(range(1,m))+list(range(m+1,n)), subset_size):
                bits = 1 
                for bit in subset:
                    bits |= 1 << bit
                res = []
                for k in subset: # 决策变量
                    next = bits & ~(1 << k)
                    res.append((C[(next, k)][0] + dists[k][m], k))
                C[(bits, m)] = min(res)

    # We're interested in all bits but the least significant (the start state)
    bits = 2**n - 1

    # Calculate optimal cost
    res = []
    for k in range(1, n):
        res.append((C[(bits & ~(1 << k), k)][0] + dists[k][0], k))
    opt, parent = min(res)

    # Backtrack to find full path
    path = []
    for i in range(n-1):
        path.append(parent)
        bits = bits & ~(1 << parent)
        _, parent = C[(bits, parent)]

    # Add implicit start state
    path.append(0)

    return opt, list(reversed(path))

def held_karp3(dists):
    n = len(dists)
    C = {}
    for k in range(1, n):
        C[(frozenset([k]), k)] = (dists[0][k], 0)
    for subset_size in range(2, n):
        for subset in itertools.combinations(range(1, n), subset_size):
            for k in subset:
                prev = frozenset(set(subset) - {k})
                res = []
                for m in subset:
                    if m == 0 or m == k:
                        continue
                    res.append((C[(prev, m)][0] + dists[m][k], m))
                C[(frozenset(subset), k)] = min(res)

    # We're interested in all bits but the least significant (the start state)
    bits = set(list(range(1,n)))

    # Calculate optimal cost
    res = []
    for k in range(1, n):
        res.append((C[(frozenset(bits), k)][0] + dists[k][0], k))
    opt, parent = min(res)

    # Backtrack to find full path
    path = []
    for i in range(n - 1):
        path.append(parent)
        new_bits = bits - {parent}
        _, parent = C[(frozenset(bits), parent)]
        bits = new_bits

    # Add implicit start state
    path.append(0)

    return opt, list(reversed(path))

简化版如下：文章来源地址https://www.toymoban.com/news/detail-742384.html

# memoization for top down recursion
memo = [[-1]*(1 << (n+1)) for _ in range(n+1)]

def fun(i, mask):
    # base case
    # if only ith bit and 1st bit is set in our mask,
    # it implies we have visited all other nodes already
    if mask == ((1 << i) | 3):
        return dist[1][i]
 
    # memoization
    if memo[i][mask] != -1:
        return memo[i][mask]
 
    res = 10**9  # result of this sub-problem
 
    # we have to travel all nodes j in mask and end the path at ith node
    # so for every node j in mask, recursively calculate cost of
    # travelling all nodes in mask
    # except i and then travel back from node j to node i taking
    # the shortest path take the minimum of all possible j nodes
    for j in range(1, n+1):
        if (mask & (1 << j)) != 0 and j != i and j != 1:
            res = min(res, fun(j, mask & (~(1 << i))) + dist[j][i])
    memo[i][mask] = res  # storing the minimum value
    return res
 
 
# Driver program to test above logic
ans = 10**9
for i in range(1, n+1):
    # try to go from node 1 visiting all nodes in between to i
    # then return from i taking the shortest route to 1
    ans = min(ans, fun(i, (1 << (n+1))-1) + dist[i][1])
 
print("The cost of most efficient tour = " + str(ans))

到了这里，关于运筹系列82：使用动态规划求解TSP问题的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！