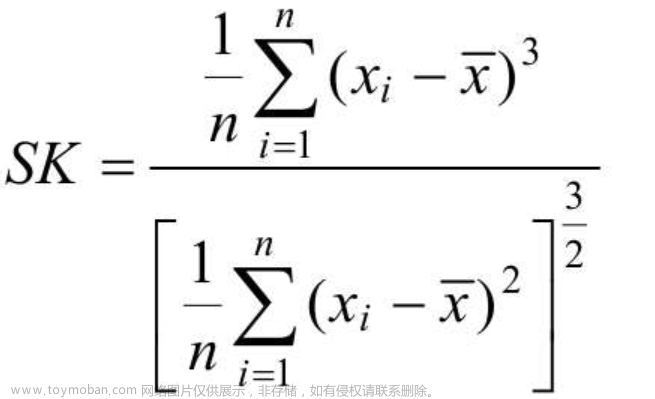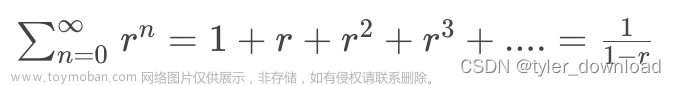Python概率论-Toy模板网

这篇具有很好参考价值的文章主要介绍了Python概率论。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

概率论是数学的一个分支，它研究随机事件的概率和统计规律。在Python中，有很多强大的概率统计库可以帮助我们进行概率计算和数据分析，比如NumPy、SciPy和Pandas等库。下面我将为您介绍一些基本的概率概念以及如何在Python中实现它们。

1. 概率的基本概念

在概率论中，我们通常会用以下的符号表示：

P(A)：表示事件A发生的概率，其取值范围在[0,1]之间。
P(A|B)：表示在事件B发生的条件下，事件A发生的概率。
P(A∪B)：表示事件A或事件B至少发生一次的概率，也叫做并集。
P(A∩B)：表示事件A和事件B同时发生的概率，也叫做交集。
P(A’)：表示事件A不发生的概率，也叫做补集。
在Python中，我们可以使用条件语句、循环语句、函数等方法来实现这些概率的计算。

2. 随机变量的概率分布

在概率论中，随机变量是一个函数，它把实验结果映射到一个实数集合上。随机变量的概率分布描述了每个取值对应的概率，通常有以下几种分布：

二项分布：描述n次独立重复实验中成功的次数的概率分布。
正态分布：描述连续变量的概率分布，也叫做高斯分布。
泊松分布：描述在一段时间内随机事件发生的次数的概率分布。
在Python中，我们可以使用scipy库来计算这些分布的概率密度函数、累积分布函数、分位数等。

3. 统计推断

统计推断是利用样本数据来推断总体分布和参数的过程。在Python中，我们可以使用Pandas库来读取和处理数据，并使用Scipy库来进行假设检验和参数估计。

具体来说，我们可以使用Pandas库中的read_csv()函数来读取csv格式的数据，然后使用Scipy库中的ttest_ind()函数来进行双样本t检验，使用pearsonr()函数来计算两个变量的相关系数等。

总之，Python是一个强大的数据分析和科学计算工具，可以帮助我们轻松地进行概率计算和数据分析。

4.程序实例

计算事件的概率

def calc_prob(event, sample_space):
    """
    计算事件的概率
    :param event: 事件，是一个集合
    :param sample_space: 样本空间，是一个集合
    :return: 概率
    """
    return len(event & sample_space) / len(sample_space)
    
# 示例
sample_space = set(range(1, 7))
event = {2, 4, 6}
print(calc_prob(event, sample_space)) # 输出0.5

计算条件概率

def cond_prob(event, condition, sample_space):
    """
    计算条件概率
    :param event: 事件，是一个集合
    :param condition: 条件，是一个集合
    :param sample_space: 样本空间，是一个集合
    :return: 条件概率
    """
    return calc_prob(event & condition, sample_space) / calc_prob(condition, sample_space)
    
# 示例
sample_space = set(range(1, 7))
event = {2, 4, 6}
condition = {2, 3, 4, 5}
print(cond_prob(event, condition, sample_space)) # 输出0.5

计算事件的并集和交集

def union(event1, event2):
    """
    计算事件的并集
    :param event1: 事件1，是一个集合
    :param event2: 事件2，是一个集合
    :return: 并集
    """
    return event1 | event2

def intersection(event1, event2):
    """
    计算事件的交集
    :param event1: 事件1，是一个集合
    :param event2: 事件2，是一个集合
    :return: 交集
    """
    return event1 & event2
    
# 示例
event1 = {1, 2, 3}
event2 = {3, 4, 5}
print(union(event1, event2)) # 输出{1, 2, 3, 4, 5}
print(intersection(event1, event2)) # 输出{3}

计算二项分布的概率

from scipy.stats import binom

def binom_prob(n, p, k):
    """
    计算二项分布的概率
    :param n: 实验次数
    :param p: 成功概率
    :param k: 成功次数
    :return: 概率
    """
    return binom.pmf(k, n, p)
    
# 示例
print(binom_prob(10, 0.5, 5)) # 输出0.24609375

计算正态分布的概率

from scipy.stats import norm

def norm_prob(x, mean, std):
    """
    计算正态分布概率密度函数在x处的概率密度值
    :param x: 横坐标
    :param mean: 正态分布的均值
    :param std: 正态分布的标准差
    :return: x处的概率密度值
    """
    return norm.pdf(x, mean, std)

print(norm_prob(1.96, 0, 1)) # 输出0.0584409443334515

模拟掷骰子

import random

def roll_dice():
    """
    模拟掷骰子
    :return: 骰子点数
    """
    return random.randint(1, 6)
    
# 示例
print(roll_dice()) # 输出1到6之间的一个整数

模拟投硬币

import random

def flip_coin():
    """
    模拟投硬币
    :return: 正面或反面
    """
    return random.choice(['H', 'T'])
    
# 示例
print(flip_coin()) # 输出'H'或'T'