1.单链表的定义
单链表解决了顺序表需要大量连续存储单元的缺点,但单链表附加指针域,存储密度较顺序表低(考点!!)。由于单链表的元素离散地分布在存储空间中,所以单链表是非随机存取的存储结构,即不能直接找到表中某个特定的结点。当查找某个特定结点时,需要从表头开始遍历。
通常使用头指针来标识一个单链表,如单链表L,头指针为NULL时表示一个空表。为了操作上的方便,可以在单链表的第一个结点之前附加一个头结点。头结点一般不存储数据,它的数据域可以不设任何信息,或记录表长等信息;头结点的指针域指向线性表的第一个元素结点。
为什么要引入头结点呢?
引入头结点后,可以带来两个优点:
①由于第一个数据结点的位置被存放在头结点的指针域中,因此在链表第一个位置上的操作和在表的其他位置上的操作一致,无须进行特殊处理。
②无论链表是否为空,其头指针都是指向头结点的非空指针(空表中头结点的指针域为空),因此空表和非空表的操作也得到了统一。
单链表的结点类型定义
typedef int ElemType;
typedef struct LNode{
ElemType data;
struct LNode *next;
}LNode, *LinkList;关于定义的几点说明:
1.在单链表的定义中不能省略结构体名称LNode(第2行中)。原因:在该结构体内部使用到了该结构体类型去定义next指针域。
2.第5行中的重命名LNode和*LinkList的意义:
这里相当于以下两句:
typedef struct LNode LNode;//将结构体重命名为LNodetypedef struct LNode *LinkList;//将结构体的指针重命名为LinkListLNode和LinkList的区别:
- LNode是一个具象的结构体类型,指向的是包含某个数据类型的数据域和指针域的结构体类型。
- 而LinkList是LNode的指针类型,它占用一定的内存空间,内存空间中存放的值是一个LNode类型结构体的地址。
2.单链表的基本操作实现
(1)头插法建立单链表
LinkList list_head_insert(LinkList &L)
{
L = (LinkList)malloc(sizeof(LNode));//申请头节点空间
L->next=NULL;
ElemType x;
scanf("%d", &x);
LNode* s;//用来指向申请的新节点
while(x!=9999)//输入9999表示结束
{
s=(LinkList)malloc(sizeof(LNode));
s->data = x;
s->next = L->next;//s的next指向原本链表的第一个节点
L->next = s;
scanf("%d", &x);
}
return L;
}【注】:这里有一个常见的错误:分配结点空间的语句
L = (LinkList)malloc(sizeof(LNode));错误写法:L = (LinkList)malloc(sizeof(LinkList));
要谨记:LinkList是LNode的指针类型,不代表结构体(该指针一般占用8个字节的空间)而这里需要的是分配的LNode大小的空间。
头插法建立单链表 时间复杂度分析
采用头插法建立单链表时,读入数据的顺序与生成的链表中的元素顺序相反。每个结点插入的时间为O(1),设单链表长为n,则总时间复杂度为O(n).
(2)尾插法建立单链表
尾插法的特点:
始终存在一个尾指针r指向链表的尾部,且读入数据的顺序与生成链表中元素的顺序相同。
LinkList list_tail_insert(LinkList &L)
{
L = (LinkList)malloc(sizeof(LNode));
L->next=NULL;
ElemType x;
scanf("%d", &x);
LNode *s, *r=L;//s用来指向申请的新节点,r始终指向链表尾部
while(x!=9999)//输入9999表示结束
{
s = (LinkList) malloc(sizeof(LNode));
s->data = x;
r->next = s;//新节点给尾节点的next指针
r=s;//r要指向新的尾部
scanf("%d", &x);
}
r->next = NULL;//让尾节点为Null
return L;
}尾插法建立单链表的时间复杂度分析
尾插法的时间复杂度与头插法相同,都是O(n)。
(3)按位查找结点
//按位置查找
LNode* GetElem(LinkList L, int SearchPos)
{
int i=0;
if(SearchPos<0)
{
return NULL;
}
while(i<SearchPos && L!=NULL)
{
L=L->next;
i++;
}
return L;
}按位查找的时间复杂度
按位查找的时间复杂度为:O(n)
(4)按值查找
LNode *LocateElem(LinkList L, ElemType e)
{
LNode *p = L->next;
while(p!=NULL && p->data!=e)
p = p->next;
return p;
}按值查找的时间复杂度
按值查找的时间复杂度为:O(n)
(5)在第i个位置上插入结点
LinkList ListFrontInsert(LinkList L, int InsertPos, ElemType InsertVal)//注意:插入不会改变链表的头节点(指针)L,和顺序表不同,这里的形参不需要使用&
{
LinkList p = GetElem(L, InsertPos-1);//GetElem函数中已自带InsertPos-1是否合法的检查
if(NULL==p)
return false;
LinkList q;
q = (LNode*) malloc(sizeof (LNode));
q->data = InsertVal;
q->next = p->next;//①
p->next = q;//②
return L;
}【注】:①②两句的顺序不能颠倒!(代码的第9和第10行)
插入结点的时间复杂度分析
插入算法的主要时间开销在于查找第i-1个元素,时间复杂度为O(n)。
若在给定的结点后面插入新结点,则时间复杂度仅为O(1).
【注】:在单链表的插入操作中,不会改变头结点指针L,因此不需要使用&类型(这一点与顺序表不同,顺序表的插入操作会改变整个表,在顺序表的插入函数中形参需要使用&)
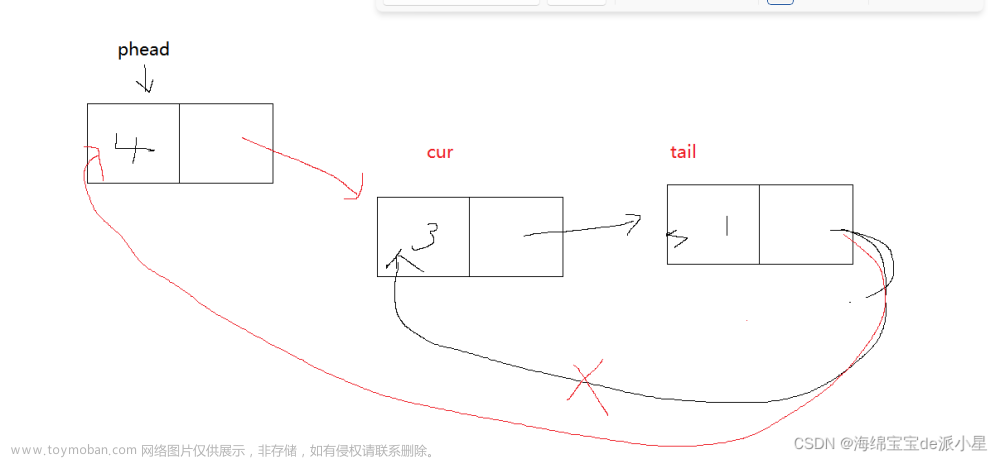
(6)删除结点操作
//删除第i个位置的元素
bool ListDelete(LinkList L, int i)
{
LinkList p= GetElem(L, i-1);
if(NULL==p)
{
return false;
}
LinkList q = p->next;
//这里可能会有疑问,如果不定义指针q,用p->next=p->next->next可以吗
//这样是不行的,因为被删除的节点没有了指针指向,无法free
p->next = q->next;//断链
free(q);//释放被删除节点的空间
}【注】:在删除节点操作中,需要定义两个指针p和q,p指向删除位置i的前一个位置的结点,p指向需要被删除的结点。这里可能会产生疑问,为什么一定要定义指针q呢?用语句p->next=p->next->next不是也可以达到删除节点的效果吗?
原因:这样是不好的!如果不定义指针q,在p->next=p->next->next之后就无法再找到删除的结点空间,无法free掉这块空间。一般前面使用malloc分配的空间在后面使用完成后都需要free掉。
删除结点的时间复杂度分析
删除结点算法的时间开销也主要在于查找第i-1个元素,时间复杂度为O(n).
整体代码演示
#include <stdio.h>
#include <stdlib.h>
typedef int ElemType;
typedef struct LNode{
ElemType data;
struct LNode *next;
}LNode, *LinkList;
//头插法新建链表
LinkList list_head_insert(LinkList &L)
L = (LinkList)malloc(sizeof(LNode));
L->next=NULL;
ElemType x;
scanf("%d", &x);
LNode* s;//用来指向申请的新节点
while(x!=9999)//输入9999表示输入结束
{
s=(LinkList)malloc(sizeof(LNode));
s->data = x;
s->next = L->next;//s的next指向原本链表的第一个节点
L->next = s;
scanf("%d", &x);
}
return L;
}
//尾插法新建链表
//尾插法的特点:定义一个尾指针r总指向链表的尾部
LinkList list_tail_insert(LinkList &L)
{
L = (LinkList)malloc(sizeof(LNode));
L->next=NULL;
ElemType x;
scanf("%d", &x);
LNode *s, *r=L;//s用来指向申请的新节点,r始终指向链表尾部
while(x!=9999)
{
s = (LinkList) malloc(sizeof(LNode));
s->data = x;
r->next = s;//新节点给尾节点的next指针
r=s;//r要指向新的尾部
scanf("%d", &x);
}
r->next = NULL;//让尾节点为Null
return L;
}
//链表打印
void print_list(LinkList L)
{
L = L->next;//没有使用引用,外面的L不会发生改变
while(L!=NULL)
{
printf("%3d", L->data);
L = L->next;
}
printf("\n");
}
//按位查找
//查找返回一个节点
LNode *GetElem(LinkList L, int SearchPos)
{
if(SearchPos<1)
{
return NULL;
}
int j=1;//计数,初始为1
LNode *p=L->next;
while(p!=NULL && j<SearchPos)
{
p=p->next;
j++;
}
return p;
}
//按值查找
LNode *LocateElem(LinkList L, ElemType e)
{
LNode *p = L->next;
while(p!=NULL && p->data!=e)
p = p->next;
return p;
}
//向第i个位置插入元素
//使用GetElem找到第i-1个节点的位置(地址、指针)
bool ListFrontInsert(LinkList L, int InsertPos, ElemType InsertVal)
{
LinkList p = GetElem(L, InsertPos-1);//GetElem函数中已自带InsertPos-1是否合法的检查
if(NULL==p)
return false;
LinkList q;
q = (LNode*) malloc(sizeof (LNode));
q->data = InsertVal;
q->next = p->next;
p->next = q;
return true;
}
//删除第i个位置的元素
bool ListDelete(LinkList L, int i)
{
//判断i的合法性已经在GetElem中定义过
//若i=1也是合法的,此时i-1=0,返回头指针
LinkList p= GetElem(L, i-1);
if(NULL==p)
{
return false;
}
LinkList q = p->next;
//此时可能会说,不定义q,用p->next=p->next->next
//这样是不行的,因为被删除的节点没有了指针指向,无法free
p->next = q->next;//断链
free(q);//释放被删除节点的空间
}
int main() {
//输入1 2 3 4 5 6 7 8 9 9999
LinkList L;//L是链表头,是结构体指针类型,大小:8个字节
// list_head_insert(L);//头插法新建链表
list_tail_insert(L);
print_list(L);
//查找
LinkList search;//查找指针
//按位置查找
search=GetElem(L, 2);//返回一个指针
if(search!=NULL)
{
printf("Succeeded in searching by serial number\n");
printf("%d\n", search->data);
}else{
printf("Failed in searching by serial number\n");
}
//按值
search=LocateElem(L, 6);
if(search!=NULL)
{
printf("Succeeded in searching by serial number\n");
printf("%d\n", search->data);
}else{
printf("Failed in searching by serial number\n");
}
//在第2个位置上插入99
bool ret;
ret=ListFrontInsert(L, 2, 99);
print_list(L);
//删除链表第4个位置的元素
ListDelete(L, 4);
print_list(L);
return 0;
}
输入:1 2 3 4 5 6 7 8 9999(用空格隔开)
实验结果:
 文章来源:https://www.toymoban.com/news/detail-742913.html
文章来源:https://www.toymoban.com/news/detail-742913.html
文章来源地址https://www.toymoban.com/news/detail-742913.html
到了这里,关于【数据结构】——单链表的基本操作(带头结点)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!