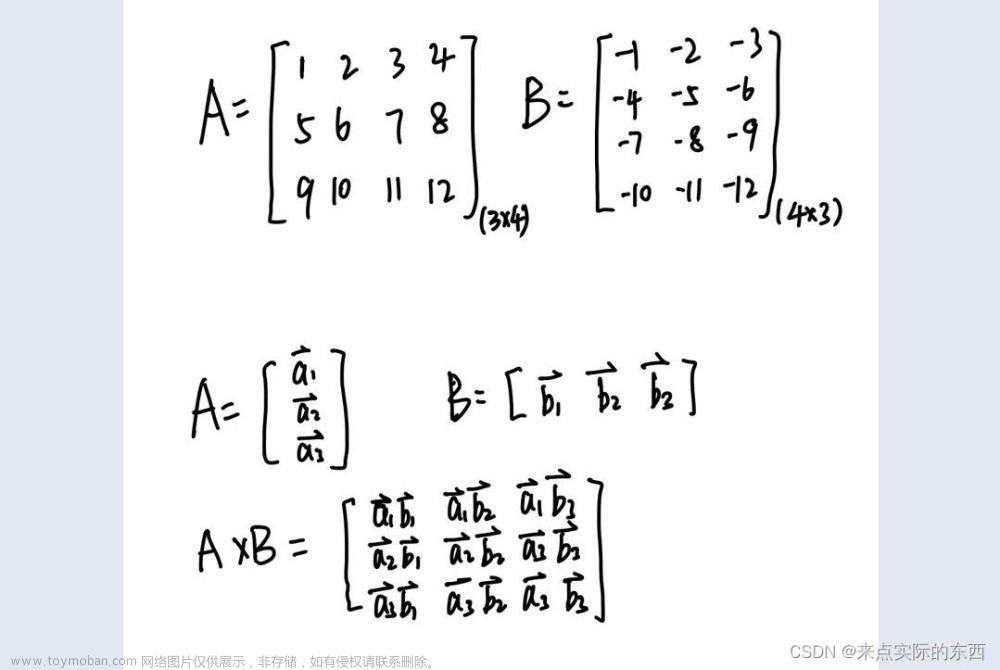
1、判断是否可以做矩阵乘法
分别求得两个矩阵的行数a1,b1以及列数a2，b2。
如果a1 == b1,并且a2 == b2则进行乘法运算文章来源：https://www.toymoban.com/news/detail-743242.html
2、C代码实现：
#include<stdio.h>
#include<assert.h>
int main(){
int a[3][3] = {{1,2,3},{2,3,4},{2,5,4}};
int b[3][3] = {{1,0,3},{0,1,4},{2,0,4}};
int len = 0;
int value1 = 0;
int k = sizeof(a[0])/sizeof(int);
//a1 = 二维数组的元素个数(行数)
int a1 = sizeof(a)/(k*sizeof(int));
//a2 = 二维数组中单个元素的长度(列数)
int a2 = k;
k = sizeof(b[0])/sizeof(int);
int b1 = sizeof(b)/(k * sizeof(int));
int b2 = k;
if(a1 != b2 && a2 != b1) {
printf("这两个矩阵不能做乘法运算：\n");
return 0;
}
int c[10][10];
//矩阵的乘法运算
for(int i = 0; i < a1;i++){
for(int j = 0;j < b2 ;j++){
for(int p = 0 ; p < a2;p++){
//行、列 元素的乘积之和
value1 += a[i][p] * b[p][j];
}
c[i][len++] = value1;
value1 = 0;
//len == a1 指的是二维数组已经到达当行的最后元素
if(len == a1){
len =0;
}
}
}
//打印矩阵乘法结果
for(int i = 0; i < k;i++){
for(int j = 0;j < k ;j++){
printf("%4d ",c[i][j]);
}
printf("\n");
}
}3、代码结果
文章来源地址https://www.toymoban.com/news/detail-743242.html
到了这里，关于矩阵乘法（C语言实现），超详细的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
