AI 人工智能之概率论基础(2)-Toy模板网

这篇具有很好参考价值的文章主要介绍了AI 人工智能之概率论基础(2)。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

设试验 E 的样本空间为 S={e} ，而 X=X(e) ， Y=Y(e) 是定义在 S={e} 上的两个随机变量成为由这两个随机变量组成的向量 (X(e),Y(e)) 为二维随机变量或者二维随机向量。

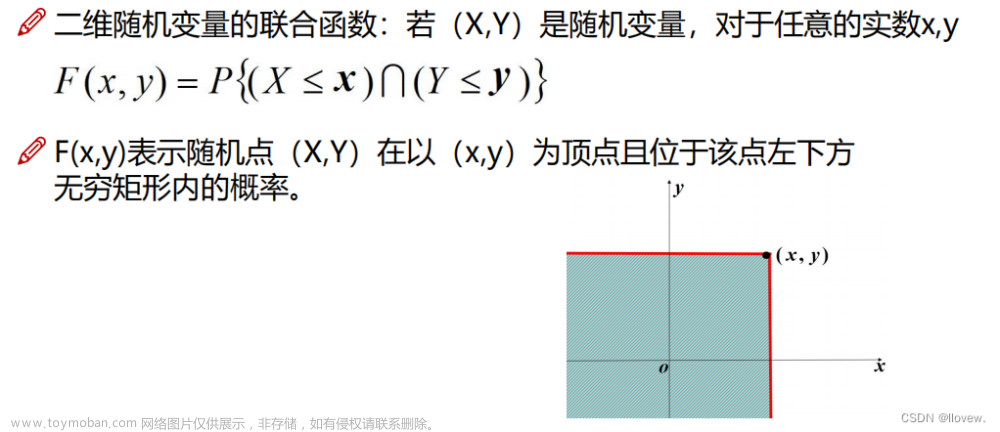
设 (X,Y) 为二维随机变量，对任意实数 x,y ，二元函数:

分布律是表还是公式,AI 人工智能,概率论,二维随机变量,联合分布,边缘分布

称为二维随机变量 (X,Y) 的分布函数，或者称为随机变量 X 和 Y 的联合分布函数。

二维随机变量分布函数具有下列五条基本性质:

分布律是表还是公式,AI 人工智能,概率论,二维随机变量,联合分布,边缘分布

若二维随机变量 (X,Y) 的所有取值为有限对或者可列对 (xi,yj) ， i,j=1,2,… ，则称 (X,Y) 是离散型随机变量。

记 P{X=xi,Y=yi}=pij, i,j=1,2,… ，则称它为二维离散型随机变量 (X,Y) 的（概率）分布律，或者称为 X 和 Y 的联合（概率）分布律。

分布律有两种常用的表示法：公式法和列表法。
这种分布律具有下面两种性质:

设（X，Y）是二维随机变量，x，y是任意实数，二元函数：

F(x,y)=P({X≤x∩Y≤y})=P(X≤x,Y≤y)，被称二维随机变量(X，Y)的分布函数，或称为X和Y的联合分布函数。

将二维随机变量（X，Y）看成是平面上随机点的坐标，分布函数F（x，y）在（x，y）处的函数值就是随机点（X，Y）落在如图以（x，y）为顶点而位于该点左下方的无穷矩形区域内的概率。文章来源地址https://www.toymoban.com/news/detail-743299.html

到了这里，关于AI 人工智能之概率论基础(2)的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

AI 人工智能之概率论基础(2)