三元组操作（相加）——稀疏矩阵（c语言）-Toy模板网

这篇具有很好参考价值的文章主要介绍了三元组操作（相加）——稀疏矩阵（c语言）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

运行环境：TDM-GCC

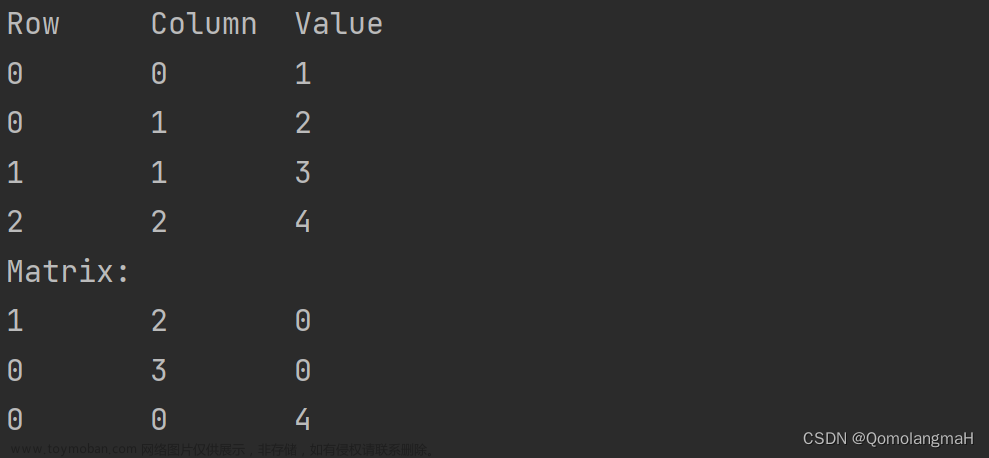
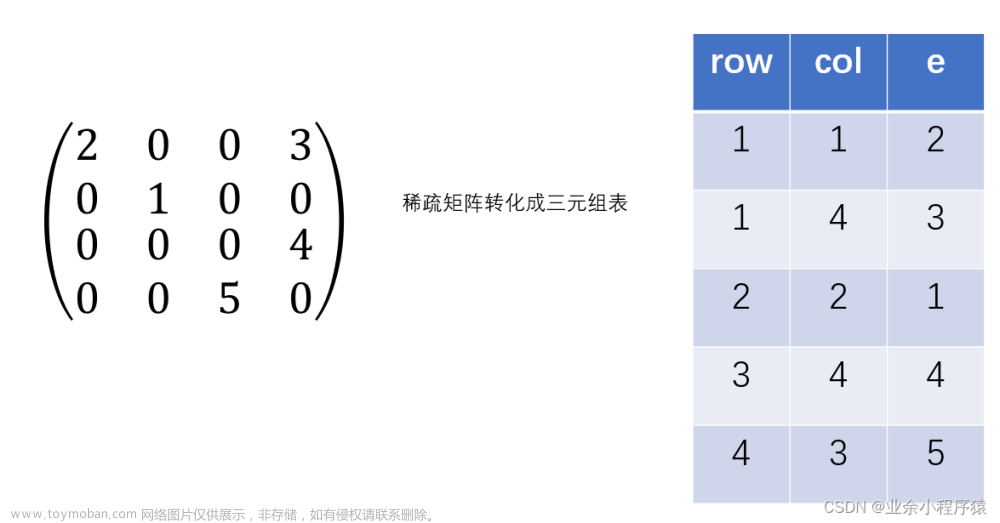
三元组用来存储稀疏矩阵比较节省空间，因为稀疏矩阵大部分都是零元素，而三元组只记录非零元素。

#include "stdio.h"
#define MaxSize 100
typedef int ElemType; 
//定义三元组线性表中的数据元素存储结构
typedef struct{
	int row;    //行号 
	int col;    //列号 
	ElemType d; //元素值，ElemType为数据元素类型学
}TripleNode;  //三元组定义

//定义三元组线性表存储结构
typedef struct{
	int rows;  //行数值 
	int cols;  //列数值 
	int nums;  //非零元素个数 
	TripleNode data[MaxSize]; //data 数据域 
}TMatrix;//三元组顺序表定义 

//以行序方式扫描二维矩阵A,将其非零的元素加入到三元组t
//以3行4列的稀疏矩阵为例
void CreatMat(TMatrix *t,int arr[3][4]) 
{
	int i;
	int j;
	t->rows = 3;
	t->cols = 4;
	t->nums = 0;
	//扫描矩阵中的非零元素
	for(i=0;i<3;i++){
		for(j=0;j<4;j++){
			//只存非零值，以三元组方式
			if(arr[i][j]!= 0)
			{
				t->data[t->nums].row = i;
				t->data[t->nums].col = j;
				t->data[t->nums].d = arr[i][j];
				t->nums++; 
			 } 
		}
	} 
}
//获取i,j位置的元素的值 ，赋值给data  执行 *data= A[i][j]
void MatrixGet(TMatrix *t,int *data,int i,int j){
	int k = 0;
	int k1;
	//指定的行或列是否合法
	if(i>=t->rows || j>= t->cols)
	return;
	while(k<t->nums && i>t->data[k].row)
	k++;
	while(k<t->nums && i==t->data[k].row && j>t->data[k].col)
	k++;
	if(t->data[k].row == i && t->data[k].col)
	{
		*data = t->data[k].d; //获取到值 
	}
	else{
		*data = 0;   //获取到值 
	}	 
}
//修改三元组元素中的值：执行A[i][j]= data
void MatrixSet(TMatrix *t,int data,int i,int j){
	int k = 0;
	int k1;
	if(i>=t->rows || j>=t->cols) 
	return;
	while(k<t->nums&&i>t->data[k].row)
	k++;
	while(k<t->nums&&i==t->data[k].row &&i>t->data[k].col)
	k++;
	//当找到指定位置时直接修改
	if(i==t->data[k].row && j==t->data[k].col) 
	{
		t->data[k].d=data; 
	}else
	{
		//如果指定位置不存在，则说明该元素值为0，此时插入
		for(k1=t->nums;k1>=k;k1--)
		{
			t->data[k1+1].col = t->data[k1].col; //后一个等于前一个，腾出一个位置给目标元素 
			t->data[k1+1].row = t->data[k1].row;
			t->data[k1+1].d = t->data[k1].d; 
		}
		//插入数据
		t->data[k].row = i;
		t->data[k].col = j;
		t->data[k].d = data;
		t->nums++; 
	}
	 
}

void MatrixAdd(TMatrix *A,TMatrix *B,TMatrix *C){
	int p =1;
	int q =1; 
	int k = 1;
	while(p<=A->nums && q<=B->nums){          //p 和 q 分别为 A 和 B 的非零元素个数 ，从1开始 
		if(A->data[p].row<B->data[q].row){    //如果A的第p元素的行号 小于 B的第q元素的行号
			C->data[k].row = A->data[p].row;  //C的第k个元素  就等于这个A 该元素。  即把A该元素（数据、行号、列号） 赋值给C 
			C->data[k].col = A->data[p].col;
			C->data[k].d = A->data[p].d;
			p++;                            //A当前p 已经完成，下一个元素 
			k++;                            //K 下一个位置 
		}else if(A->data[p].row == B->data[q].row){   //如果某元素的行数相等 ，那进一步看列 
		
			if(A->data[p].col<B->data[q].col){     //A的该元素的列 小于  B的元素的列           //C需要保留这个位置 
				C->data[k].d = A->data[p].d;       //把A的该元素（数据、行号、列号） 赋值给C        
				C->data[k].row = A->data[p].row;
				C->data[k].col = A->data[p].col;
				p++;                               //A的下一个 
				k++;                                 
			}else if(A->data[p].col == B->data[q].col){  //A的该元素的列 等于  B的元素的列           //这个时候需要相加元素的值 
				C->data[k].d = A->data[p].d + B->data[q].d;
				C->data[k].row = A->data[p].row;
				C->data[k].col = A->data[p].col;
				p++;
				k++;
				q++;
			}else{
				C->data[k].row = B->data[q].row;
				C->data[k].col = B->data[q].col;
				C->data[k].d = B->data[q].d;
				q++;
				k++;	 
			}
		}
		else{
			C->data[k].d = B->data[q].d;
			C->data[k].row = B->data[q].row;
			C->data[k].col = B->data[q].col; 
			q++;
			k++; 
		}
	}
	while(p<=A->nums){      //p没有进行完，说明A里面还有元素，直接弄到C里面就好 
		C->data[k] = A->data[p];
		p++;
		k++; 
	} 
	while(q<=B->nums){      //q没有进行完，说明B里面还有元素，直接弄到C里面就好 
		C->data[k] = B->data[q];
		q++;
		k++;
	}
	C->nums = k-1;
	C->cols = A->cols;  // 两个矩阵 同型  
	C->rows = A->rows; 
} 

//输出元素值
void DispMat(TMatrix *t){
	int i;
	if(t->nums <=0)
	{
		return;
	}
	printf("\n\t行数：%d\t列数:%d\t元素个数：%d\n",t->rows,t->cols,t->nums);
	printf("\t--------------------\n");
	//输出所有的三元组
	for(i=0;i<t->nums;i++)
	{
		printf("\t第%d 行\t第%d 列\t%d\n",t->data[i].row,t->data[i].col,t->data[i].d);
	 } 
} 


int main(void)
{
    //通过自定义3行4列的二维数组来表示稀疏矩阵
    int arrA[3][4] = {
                    {0 , 1 , 0 , 0},
                    {0 , 0 , 0 , 2},
                    {3 , 0 , 0 , 4}
                    };
    int arrB[3][4] = {
                {1 , 0 , 2 , 2},
                {0 , 0 , 3 , 2},
                {3 , 0 , 7 , 4}
                };

    int data = 0;
    TMatrix ta = {0};
    TMatrix tb = {0};
    TMatrix tc = {0};
    CreatMat(&ta , arrA);
    CreatMat(&tb , arrB);
    //输出三元组
    DispMat(&ta);
    DispMat(&tb);
    DispMat(&tc);
    MatrixAdd(&ta , &tb , &tc);
    //输出三元组
    printf("\n______________________________________\n");
    DispMat(&tc);
    return 0;
}

这里两个相加的矩阵有着同样的 i行 j列。

运行结果：

行数：3 列数:4 元素个数：4
--------------------
第0 行第1 列 1
第1 行第3 列 2
第2 行第0 列 3
第2 行第3 列 4

行数：3 列数:4 元素个数：8
--------------------
第0 行第0 列 1
第0 行第2 列 2
第0 行第3 列 2
第1 行第2 列 3
第1 行第3 列 2
第2 行第0 列 3
第2 行第2 列 7
第2 行第3 列 4

______________________________________

行数：3 列数:4 元素个数：8
--------------------
第0 行第0 列 0
第0 行第2 列 2
第0 行第3 列 2
第1 行第2 列 3
第1 行第3 列 4
第2 行第0 列 6
第2 行第2 列 7
第2 行第3 列 8

--------------------------------文章来源地址https://www.toymoban.com/news/detail-743399.html