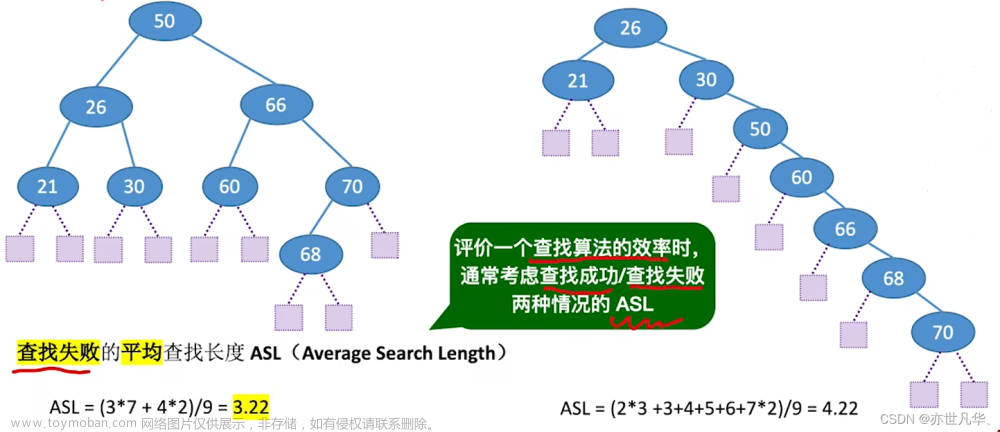
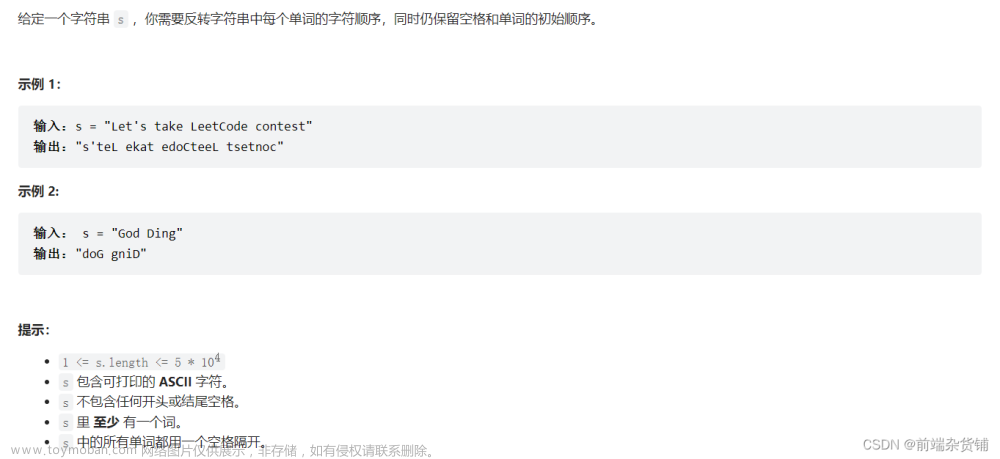
solution
欧拉函数法可以解决模幂运算文章来源:https://www.toymoban.com/news/detail-743706.html
#include<stdio.h>
#include<math.h>
int main(){
int a, m, n, r=1;
scanf("%d%d%d", &a, &m, &n);
while(m){
if(m&1) r=(r*a)%n;
a=(a*a)%n;
m>>=1;
}
printf("%d", r);
return 0;
}
给定伪代码的思想文章来源地址https://www.toymoban.com/news/detail-743706.html
#include<stdio.h>
#include<math.h>
int isPrime(int n){
for(int i = 2; i <= sqrt(n); i++){
if(n % i == 0) return 0;
}
return 1;
}
int gcd(int a, int b){
int temp;
while(a){
temp = a;
a = b % a;
b = temp;
}
return b;
}
int main(){
int a, m, n, count = 0, c = 1, z[35], num = 0, t;
scanf("%d%d%d", &a, &m, &n);
if(isPrime(n) && gcd(a, n) == 1 && m >= n){
m%= n-1;
}
t = m;
do{
z[num++] = t % 2;
t /= 2;
if(z[num-1]) count++;
}while(t != 0);
for(int j = num - 1; j >= 0; j--){
c = (c*c) % n;
if(z[j]) c = (a*c) % n;
}
printf("%d %d", c, count);
return 0;
}
到了这里,关于7-2 数论中的模幂运算的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!