编译原理实验二——消除文法的左递归(c++实现)
首先给出书中的算法截图:
第一步:处理产生式的输入
所有产生式使用一个结构体存储:
struct node
{
string left;
set<string>right;
};
可以看到,left代表产生式的左部,right代表产生式的右部,而且是一个集合。
例如S->Qc|c,在程序中,left=S,right=Qc,c
输入的结果保存在一个vector的数据结构中,并起名为v
输入函数为:
void getproduction()
{
printf("若一个非终结符可推出多个结果,请直接以 | 分隔,不必分开输入\n");
printf("输入产生式,以$为结束标志:\n");
string str;
while (cin >> str && str[0] != '$')
{
vector<node>ret = mysplit(str);
v.push_back(ret[0]);
}
}
由于输入是一整行字符串,所以我们需要根据字符将产生式的左部和右部的结果剥离出来,在这里调用mysplit()函数。下面是mysplit()函数的具体代码。
vector<node> mysplit(string str)
{
string vleft;
set<string>vright;
string temp = "";
for (int i = 0; i < str.size(); i++)
{
if (str[i] == '>')continue;
if (str[i] == '-')
{
vleft=temp;
temp = "";
continue;
}
if (str[i] == '|')
{
vright.insert(temp);
temp = "";
continue;
}
temp += str[i];
}
if (temp != "")vright.insert(temp);
vector<node>ret;
struct node N = {vleft,vright};
ret.push_back(N);
return ret;
}
代码原理很简单,直接遍历字符串,遇到-,>,| 等特殊字符就对应插入left或right中。
第二步:获取所有非终结符,并排序
void getnotend()
{
set<string>tempset;
for (int i = 0; i < v.size(); i++)
{
tempset.insert(v[i].left);
}
set<string>::iterator it = tempset.begin();
for (it; it != tempset.end(); it++)
{
notend.push_back(*it);
}
}
getnotend()函数获取了所有的非终结符。直接遍历v中保存的所有产生式的左部,存入set中。
(v是保存了所有产生式的变量名,为vector类型)
所有的非终结符被保存在notend中,其定义为vector类型
第三步:两层for循环,在这里封装成了myoperate()函数。
void myoperate()
{
for (int i = 0; i < notend.size(); i++)//FOR i:=1 TO N DO
{
for (int j = 0; j < i; j++)//FOR j:=1 TO i-1 DO
{
int posi=-1, posj=-1;
for (int k = 0; k < v.size(); k++)
{
if (v[k].left == notend[i])/*遍历所有产生式,找到第i个非终结符在所有产生式中的位置*/
{
posi = k;
break;
}
}
for (int k = 0; k < v.size(); k++)/*遍历所有产生式,找到第i个非终结符在所有产生式中的位置*/
{
if (v[k].left == notend[j])
{
posj = k;
break;
}
}
if (posi == -1 || posj == -1)continue;/*如果找不到,就不执行下面的代码。例如:非终结符S在v中是第3个,非终结符R在v中是第1个,则posi=3,posj=1*/
set<string>::iterator it = v[posi].right.begin();
set<string>::iterator it2 ;
set<string>tempset;
for (it; it != v[posi].right.end(); it++)
{
string tempstr = *it;
string ss;
if (tempstr.find(notend[j]) != -1)
{
for (it2 = v[posj].right.begin(); it2 !=v[posj].right.end(); it2++)
{
ss = tempstr;
ss = myreplace(ss, notend[j], *it2);
tempset.insert(ss);
}
}
}
vector<string>temv;
for (it = v[posi].right.begin(); it != v[posi].right.end(); it++)
{
string str = *it;
if (str.find(notend[j]) != -1)
temv.push_back(str);
}
for (int x = 0; x < temv.size(); x++)
{
it = v[posi].right.find(temv[x]);
if (it != v[posi].right.end())
v[posi].right.erase(it);
}
for (it = tempset.begin(); it != tempset.end(); it++)
v[posi].right.insert(*it);
erasedirect(posi);
}
}
}
在这里给出此函数的解释,代码中使用了许多临时变量记录信息。但整体思路如下:
以书本中给出的例子,有一个文法:
(1)S->Qc|c
(2) Q->Rb|b
(3) R->Sa|a
求它消除左递归的最终文法。
由于代码中下标从0开始,当i=2,j=0时,我们看第(1),第(3)个产生式。我们拿出第(3)个产生式的所有右部,得到 Sa和a。对每一个右部,若它有第j个非终结符,就可以把第j个终结符可以推出的所有结果拿来替换。
比如,我们拿出Sa,发现它有第j个非终结符S,所以S可以推出的所有结果都可以换到Sa身上,Sa就可以变成Qca和ca. 然后,我们拿出a,发现它没有S,直接跳过。最后,R->Qca|ca|a,也就是书中的答案。
代码中已对一些细节做了考虑,具体参考代码。
第四步:消除Ai中的一切直接左递归
首先,直接左递归见书中的定义:

A->Aa1|Aa2|…|Aam|b1|b2|b3|b3
那么,我们就看产生式是不是满足这种形式
首先如何判断b1,b2,b3?
如果右部没有大写字母,就可以认为它是b1,b2,b3
因此,有了下面的函数:
bool allend(string str)
{
for (int i = 0; i < str.size(); i++)
{
if (str[i] >= 'A' && str[i] <= 'Z')
return false;
}
return true;
}
如何判断右部是与左部一样的字符串开头呢
首先给出c++字符串查找函数find(),rfind()。
find()可以从前往后找,找到第一个匹配的字符串,返回下标,如果找不到,返回-1
rfind()可以从后往前找,找到第一个匹配的字符串,返回下标,如果找不到,返回-1
那么,我们可以从前往后找,再从后往前找,如果遇到的第一个匹配字符都是下标为0,说明符合
A->Aa这种形式。比如 A->AabcA, find()的结果是0,rfing()的结果是4。
下面给出消除一切直接左递归的代码
void erasedirect(int posi)
{
set<string>::iterator it = v[posi].right.begin();
bool flag = true;
for (it; it != v[posi].right.end(); it++)
{
string str = *it;
if ((str.find(v[posi].left) == str.rfind(v[posi].left) && str.find(v[posi].left) == 0) || allend(str))
flag = true;
else
{
flag = false;
break;
}
}
if (!flag)return;
vector<string>va, vb;
for (it = v[posi].right.begin(); it != v[posi].right.end(); it++)
{
string str = *it;
if (str.find(v[posi].left) == -1)
{
vb.push_back(str);
}
else
{
str.erase(0, v[posi].left.size());
va.push_back(str);
}
}
v[posi].right.clear();
for (int i = 0; i < vb.size(); i++)
{
v[posi].right.insert(vb[i] + v[posi].left+"'");
}
set<string>ans;
for (int i = 0; i < va.size(); i++)
{
ans.insert(va[i] + v[posi].left + "'");
}
ans.insert("Σ");
struct node N = { v[posi].left + "'",ans };
v.push_back(N);
}
首先我们确定Ai的产生式是不是满足A->Aa|b这种形式,如果不是,flag=false,直接结束运行,否则,继续往下做。
当我们确定Ai推出的式子都是Aa或b后,我们可以遍历Ai的所有右部,把Aa的抠出来,存在va中,b抠出来,存在vb中,然后字符串拼接答案,给非终结符加上一撇,就可以了。
最后给出完整的可运行代码:
#include<iostream>
#include<cmath>
#include<algorithm>
#include<map>
#include<vector>
#include<unordered_map>
#include<set>
using namespace std;
struct node
{
string left;
set<string>right;
};
vector<node>v;
vector<string>notend;
bool allend(string str)
{
for (int i = 0; i < str.size(); i++)
{
if (str[i] >= 'A' && str[i] <= 'Z')
return false;
}
return true;
}
void getnotend()
{
set<string>tempset;
for (int i = 0; i < v.size(); i++)
{
tempset.insert(v[i].left);
}
set<string>::iterator it = tempset.begin();
for (it; it != tempset.end(); it++)
{
notend.push_back(*it);
}
}
vector<node> mysplit(string str)
{
string vleft;
set<string>vright;
string temp = "";
for (int i = 0; i < str.size(); i++)
{
if (str[i] == '>')continue;
if (str[i] == '-')
{
vleft=temp;
temp = "";
continue;
}
if (str[i] == '|')
{
vright.insert(temp);
temp = "";
continue;
}
temp += str[i];
}
if (temp != "")vright.insert(temp);
vector<node>ret;
struct node N = {vleft,vright};
ret.push_back(N);
return ret;
}
void getproduction()
{
printf("若一个非终结符可推出多个结果,请直接以 | 分隔,不必分开输入\n");
printf("输入产生式,以$为结束标志:\n");
string str;
while (cin >> str && str[0] != '$')
{
vector<node>ret = mysplit(str);
v.push_back(ret[0]);
}
}
string myreplace(string str, string s,string t)
{
while (str.find(s) != -1)
{
int pos = str.find(s);
str.replace(pos, s.size(), t);
}
return str;
}
void erasedirect(int posi)
{
set<string>::iterator it = v[posi].right.begin();
bool flag = true;
for (it; it != v[posi].right.end(); it++)
{
string str = *it;
if ((str.find(v[posi].left) == str.rfind(v[posi].left) && str.find(v[posi].left) == 0) || allend(str))
flag = true;
else
{
flag = false;
break;
}
}
if (!flag)return;
vector<string>va, vb;
for (it = v[posi].right.begin(); it != v[posi].right.end(); it++)
{
string str = *it;
if (str.find(v[posi].left) == -1)
{
vb.push_back(str);
}
else
{
str.erase(0, v[posi].left.size());
va.push_back(str);
}
}
v[posi].right.clear();
for (int i = 0; i < vb.size(); i++)
{
v[posi].right.insert(vb[i] + v[posi].left+"'");
}
set<string>ans;
for (int i = 0; i < va.size(); i++)
{
ans.insert(va[i] + v[posi].left + "'");
}
ans.insert("Σ");
struct node N = { v[posi].left + "'",ans };
v.push_back(N);
}
void myoperate()
{
for (int i = 0; i < notend.size(); i++)//FOR i:=1 TO N DO
{
for (int j = 0; j < i; j++)//FOR j:=1 TO i-1 DO
{
int posi=-1, posj=-1;
for (int k = 0; k < v.size(); k++)
{
if (v[k].left == notend[i])/*遍历所有产生式,找到第i个非终结符在所有产生式中的位置*/
{
posi = k;
break;
}
}
for (int k = 0; k < v.size(); k++)/*遍历所有产生式,找到第i个非终结符在所有产生式中的位置*/
{
if (v[k].left == notend[j])
{
posj = k;
break;
}
}
if (posi == -1 || posj == -1)continue;/*如果找不到,就不执行下面的代码。例如:非终结符S在v中是第3个,非终结符R在v中是第1个,则posi=3,posj=1*/
set<string>::iterator it = v[posi].right.begin();
set<string>::iterator it2 ;
set<string>tempset;
for (it; it != v[posi].right.end(); it++)
{
string tempstr = *it;
string ss;
if (tempstr.find(notend[j]) != -1)
{
for (it2 = v[posj].right.begin(); it2 !=v[posj].right.end(); it2++)
{
ss = tempstr;
ss = myreplace(ss, notend[j], *it2);
tempset.insert(ss);
}
}
}
vector<string>temv;
for (it = v[posi].right.begin(); it != v[posi].right.end(); it++)
{
string str = *it;
if (str.find(notend[j]) != -1)
temv.push_back(str);
}
for (int x = 0; x < temv.size(); x++)
{
it = v[posi].right.find(temv[x]);
if (it != v[posi].right.end())
v[posi].right.erase(it);
}
for (it = tempset.begin(); it != tempset.end(); it++)
v[posi].right.insert(*it);
erasedirect(posi);
}
}
}
int main()
{
getproduction();
getnotend();
/*notend.push_back("S");
notend.push_back("Q");
notend.push_back("R");*/
myoperate();
printf("消除一切左递归后的结果为:\n");
for (int i = 0; i < v.size(); i++)
{
cout << v[i].left << "->";
set<string>::iterator it = v[i].right.begin();
int cnt = 0;
for (it; it != v[i].right.end(); it++)
{
cout << *it;
cnt++;
if (cnt != v[i].right.size())
cout << '|';
}
cout << endl;
}
return 0;
}
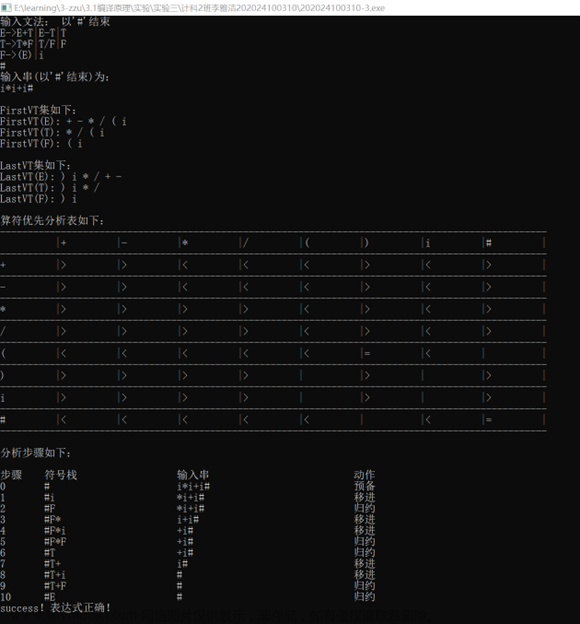
测试用例是书中原题:
(1)S->Qc|c
(2) Q->Rb|b
(3) R->Sa|a
求它消除左递归的最终文法。
给出输入:
S->Qc|c
Q->Rb|b
R->Sa|a
$
运行结果:
这个答案和书中给出的不一样,这是因为notend(非终结符)中的排序结果是按字典序从小到大排的,结果是Q,R,S。
下面我们强制给notend输入顺序为S,Q,R,只需注释掉获取非终结符的函数getnotend(),手动给出顺序为S,Q,R即可。
结果和书中给出的一样!
书中也给出了R,Q,S的顺序,我们同样进行验证文章来源:https://www.toymoban.com/news/detail-744046.html

答案仍然一样!文章来源地址https://www.toymoban.com/news/detail-744046.html
到了这里,关于编译原理实验二——消除一切文法的左递归(c++实现)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!