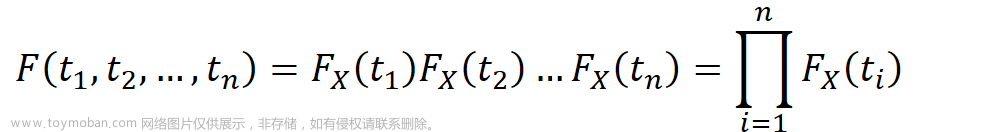【学习记录】数理统计三大分布

8月前作者：惊岁晚分类：Toy博客阅读(31) 违法举报

这篇具有很好参考价值的文章主要介绍了【学习记录】数理统计三大分布。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

刚开始学时做的笔记，有一些式子是后面参数估计时用到的，写在这里感觉没头没尾的，有一些也没讲清楚，但还是传上来保存记录，等全部复习完了再来修改吧。

一．基于正态分布演化的三大分布

1. 卡方分布

2. F分布

3. t分布

二．定理证明

5.4.1 数理统计f分布,数理统计补完计划,概率论,算法

①书本证明

②非书本证明

i基础知识

ii类似结论

iii大致证明节点

5.4.3 数理统计f分布,数理统计补完计划,概率论,算法

5.4.4 数理统计f分布,数理统计补完计划,概率论,算法

三．总结

三大统计量构成及分位数查表总结

三大统计量相互转换

一．基于正态分布的三大分布

1.卡方分布

描述：呈正偏态（右偏态），具可加性，由n个服从正态分布的统计量的平方相加构成，n-1为自由度。

图：

中心极限定理：n变大，图接近正态分布

数理统计f分布,数理统计补完计划,概率论,算法

单侧分位数和双侧分位数

数理统计f分布,数理统计补完计划,概率论,算法

2.F分布

数理统计f分布,数理统计补完计划,概率论,算法

数理统计f分布,数理统计补完计划,概率论,算法

3.t分布

数理统计f分布,数理统计补完计划,概率论,算法

数理统计f分布,数理统计补完计划,概率论,算法

二.定理证明

5.4.1

前提：

数理统计f分布,数理统计补完计划,概率论,算法

第三条的证明：数理统计f分布,数理统计补完计划,概率论,算法

（常用公式，在参数估计时用于构建T统计量）

①书本证明

数理统计f分布,数理统计补完计划,概率论,算法

数理统计f分布,数理统计补完计划,概率论,算法

②非书本证明

来自：

一文弄懂为啥(n-1)s^2/σ^2是服从n-1个自由度的卡方分布（正交变换的应用） - 知乎 (zhihu.com)

i基础知识

数理统计f分布,数理统计补完计划,概率论,算法

ii类似结论

数理统计f分布,数理统计补完计划,概率论,算法

iii大致证明节点

数理统计f分布,数理统计补完计划,概率论,算法

5.4.3

数理统计f分布,数理统计补完计划,概率论,算法

证明如下：

1. 数理统计f分布,数理统计补完计划,概率论,算法

2. 数理统计f分布,数理统计补完计划,概率论,算法

3.

数理统计f分布,数理统计补完计划,概率论,算法

5.4.4

数理统计f分布,数理统计补完计划,概率论,算法

在5.4.3基础上，设数理统计f分布,数理统计补完计划,概率论,算法

和数理统计f分布,数理统计补完计划,概率论,算法

则：数理统计f分布,数理统计补完计划,概率论,算法

理论支持：卡方分布的可加性

证明过程：

数理统计f分布,数理统计补完计划,概率论,算法

数理统计f分布,数理统计补完计划,概率论,算法

三．总结

三大统计量构成及分位数查表总结

数理统计f分布,数理统计补完计划,概率论,算法

数理统计f分布,数理统计补完计划,概率论,算法

三大统计量相互转换

1.

数理统计f分布,数理统计补完计划,概率论,算法

2. 数理统计f分布,数理统计补完计划,概率论,算法

数理统计f分布,数理统计补完计划,概率论,算法

数理统计f分布,数理统计补完计划,概率论,算法

数理统计f分布,数理统计补完计划,概率论,算法

数理统计f分布,数理统计补完计划,概率论,算法

卡方分布的可加性

资料来自CSDN论坛，茆诗松.概率论与数理统计教程（第三版）以及老师的PPT。

删水印参考：

CSDN博客图片水印自定义及去除方法 - XavierJ - 博客园 (cnblogs.com)

为什么明明有水印但是属性里显示没有，只能加水印不能去水印吗我靠文章来源地址https://www.toymoban.com/news/detail-744139.html

到了这里，关于【学习记录】数理统计三大分布的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：

领支付宝红包赞助服务器费用

《概率论与数理统计》学习笔记6-样本及样本函数的分布

目录总体简单随机样本直方图样本分布函数样本函数及其概率分布 𝜒2分布 𝑡分布 𝐹分布总体：研究对象的全体个体：总体中的每一个元素总体容量：总体

2024年02月08日
浏览(29)
概率论与数理统计---随机变量的分布

随机变量随机变量就是随机事件的数值体现。例如投色子记录色子的点数，记录的点数其实就是一个随机变量，他是这个点数出现的数值体现。注意：随机变量X = X(e) , 是一个单实值函数，每个随机事件的结果只能对应一个随机变量。 X(e)体现的是对随机事件的描述，本质

2024年02月13日
浏览(31)
概率论与数理统计————3.随机变量及其分布

设E是一个随机试验，S为样本空间，样本空间的任意样本点e可以通过特定的对应法则X，使得每个样本点都有与之对应的数对应，则称 X=X（e）为随机变量分布函数：设X为随机变量，x是任意实数，则事件{Xx}为随机变量X的分布函数，记为F（x）即： F（x）=P（Xx）（1）几何意

2024年01月18日
浏览(31)
概率论与数理统计（3）--指数分布函数及其期望、方差

设随机变量X具有如下形式的密度函数，那么则称X服从参数为θ的指数分布, 记为X~EXP(θ). 指数分布的分布函数为： ①数学期望如果X 服从参数为λ (λ0)的指数分布,那么指数分布X~EXP(θ)的数学期望： λ ②方差设X 服从参数为λ (λ0)的指数分布, 指数分布X~EXP(θ)的方差：λ^2。

2024年02月11日
浏览(30)
概率论与数理统计：第二、三章:一维~n维随机变量及其分布

1.随机变量 ①X=X(ω) ②一般用大写字母表示常见的两类随机变量——离散型随机变量、连续型随机变量 2. 分布函数 F ( x ) F(x) F ( x ) (1)定义 1.定义：称函数 F ( x ) = P { X ≤ x } ( − ∞ x + ∞ ) F(x)=P{ X≤x} (-∞x+∞) F ( x ) = P { X ≤ x } ( − ∞ x + ∞ ) 为随机变量X的分布函数，

2024年02月13日
浏览(32)
概率论与数理统计：正态分布相关推论及推导（更新ing）

统计量： X ‾ = 1 n ∑ i = 1 n X i ，其中 X i ~ N ( μ , σ 2 ) overline{X}= cfrac{1}{n}sum_{i=1}^nX_{i}，其中X_{i}text{textasciitilde} N(mu,{sigma^{2}} ) X = n 1 i = 1 ∑ n X i ，其中 X i ~ N ( μ , σ 2 ) S 2 = 1 n − 1 ∑ i = 1 n ( X i − X ‾ ) 2 S^2= cfrac{1}{n-1}sum_{i=1}^n(X_{i}-overline{X})^2 S 2 = n −

2024年02月07日
浏览(34)
2.带你入门matlab数理统计常见分布的概率密度函数（matlab程序）

1. 简述计算概率分布律及密度函数值 matlab直接提供了通用的计算概率密度函数值的函数，它们是pdf 和namepdf函数，使用方式如下： Y=pdf(‘name’，K，A，B)或者：namepdf (K，A，B) 上述函数表示返回在X=K处、参数为A、B、C的概率值或密度值，对于不同的分布，参数个数是不

2024年02月03日
浏览(26)
概率论与数理统计中常见的随机变量分布律、数学期望、方差及其介绍

设随机变量X的所有可能取值为0与1两个值，其分布律为若分布律如上所示，则称X服从以P为参数的(0-1)分布或两点分布。记作X~ B(1，p) 0-1分布的分布律利用表格法表示为: X 0 1 P 1-P P 0-1分布的数学期望 E(X) = 0 * (1 - p) + 1 * p = p 二项分布的分布律如下所示：其中P是事件在一次试验

2024年02月05日
浏览(31)
【考研数学】概率论与数理统计 —— 第三章 | 二维随机变量及其分布（3，二维随机变量函数的分布）

设 ( X , Y ) (X,Y) ( X , Y ) 为二维随机变量，以 X , Y X,Y X , Y 为变量所构成的二元函数 Z = φ ( X , Y ) Z=varphi(X,Y) Z = φ ( X , Y ) ，称为随机变量 ( X , Y ) (X,Y) ( X , Y ) 的函数，其分布一般有如下几种情形： ( X , Y ) (X,Y) ( X , Y ) 为二维离散型随机变量设 ( X , Y ) (X,Y) ( X , Y ) 联合分布律为

2024年02月07日
浏览(28)
概率论与数理统计：Ch2.一维随机变量及其分布 Ch3.二维随机变量及其分布

1.随机变量 ①X=X(ω) ②一般用大写字母表示常见的两类随机变量——离散型随机变量、连续型随机变量 2. 分布函数 F ( x ) F(x) F ( x ) (1)定义 1.定义：称函数 F ( x ) = P { X ≤ x } ( − ∞ x + ∞ ) F(x)=P{ X≤x} (-∞x+∞) F ( x ) = P { X ≤ x } ( − ∞ x + ∞ ) 为随机变量X的分布函数，

2024年02月03日
浏览(39)