矩阵等价和向量组等价的一些问题

8月前作者：晴落分类：Toy博客阅读(29) 违法举报

这篇具有很好参考价值的文章主要介绍了矩阵等价和向量组等价的一些问题。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

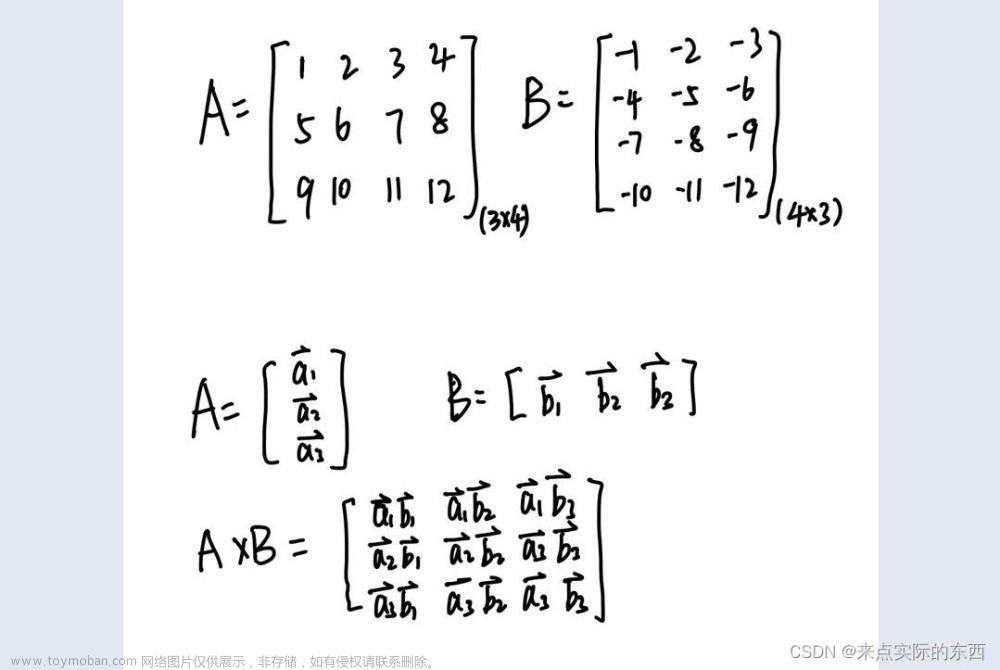
什么是向量组？答：向量组是由若干同维数的列向量（或同维数的行向量）组成的集合。
什么是向量组等价？答：两个向量组，各自拼成矩阵A和B，向量组等价就是三秩相等，即r（A）=r(B)=r（A,B）。注意：下面的例子有行向量组怎么拼成矩阵的说明
什么是矩阵等价?答：矩阵等价是同型矩阵且矩阵的秩相等。补充：对于一个矩阵来说，必有矩阵的秩=行向量组的秩=列向量组的秩
矩阵等价和向量组等价的关系是什么？可以互推吗？
答：这里其实可以有许多结论，我想了如下几个

两个矩阵等价，且都是行满秩，那么它们的列向量组必等价
两个矩阵等价，且都是列满秩，那么它们的行向量组必等价
两个矩阵等价，无其他说明，不能推出来行向量组或列向量组等价
方阵等价且满秩，那么行列向量组等价
方阵等价，无其他说明，不能推出来行向量组或列向量组等价
向量组等价，它们构成的矩阵不一定等价（不一定是同型矩阵）

矩阵等价和向量组等价的一些问题,线性代数,矩阵,算法,人工智能

矩阵等价和向量组等价的一些问题,线性代数,矩阵,算法,人工智能

矩阵等价和向量组等价的一些问题,线性代数,矩阵,算法,人工智能

矩阵等价和向量组等价的一些问题,线性代数,矩阵,算法,人工智能文章来源地址https://www.toymoban.com/news/detail-744275.html

个人理解，并未在书中找到相关结论加以验证，仅供参考

到了这里，关于矩阵等价和向量组等价的一些问题的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：

领支付宝红包赞助服务器费用

【JS 线性代数算法之向量与矩阵】

线性代数是数学的一个分支，用于研究线性方程组及其解的性质、向量空间及其变换的性质等。在计算机科学领域中，线性代数常用于图形学、机器学习、计算机视觉等领域。本文将详细介绍 JS 中常用的线性代数算法，并提供代码示例。向量是有大小和方向的量，通常用一

2024年02月13日
浏览(40)
线性代数矩阵乘法中的行向量和列向量

在矩阵中有两个概念，行向量与列向量，这是从两个不同的角度看待矩阵的组成。这篇文章将从行向量和列向量两个角度来分解矩阵的乘法。假设有两个矩阵 A 和 B 一般矩阵的乘法分解简单的理解就是A矩阵的第一行与B矩阵的第一列逐元素相乘，就是结果矩阵的左上角

2024年02月11日
浏览(34)
线性代数拾遗（6）—— 向量空间投影与投影矩阵

参考：麻省理工线性代数阅读本文前请先了解矩阵四个基本子空间，参考：线性代数拾遗（5） —— 矩阵的四个基本子空间考察二维平面投影，如下将向量 b pmb{b} b 投影到向量 a pmb{a} a 方向，得到 a pmb{a} a 的子空间中的向量 p pmb{p} p ，假设是 a pmb{a} a 的 x x x 倍如图可见

2024年02月07日
浏览(39)
线性代数｜证明：矩阵不同特征值对应的特征向量线性无关

定理 1 设 λ 1 , λ 2 , ⋯ , λ m lambda_1,lambda_2,cdots,lambda_m λ 1 , λ 2 , ⋯ , λ m 是方阵 A boldsymbol{A} A 的 m m m 个特征值， p 1 , p 2 , ⋯ , p m boldsymbol{p}_1,boldsymbol{p}_2,cdots,boldsymbol{p}_m p 1 , p 2 , ⋯ , p m 依次是与之对应的特征向量，如果 λ 1 , λ 2 , ⋯ , λ

2024年02月07日
浏览(46)
线性代数的学习和整理13: 函数与向量/矩阵

目录 1 函数与向量/矩阵 2 初等数学的函数 2.1 函数 2.2 函数的定义：定义域 →映射→ 值域 3 高等数学里的函数：定义域和陪域/到达域（非值域）的映射关系 3.1 函数 3.2 单射，满射，双射等都是针对定义域和陪域的 3.3 易错地方：值域较小且是被决定的 3.4 单射，满射，

2024年02月11日
浏览(51)
线性代数（五） | 矩阵对角化特征值特征向量

矩阵实际上是一种变换,是一种旋转伸缩变换（方阵）不是方阵的话还有可能是一种升维和降维的变换直观理解可以看系列超赞视频线性代数-哔哩哔哩_Bilibili 比如A= ( 1 2 2 1 ) begin{pmatrix}12\\\\21end{pmatrix} ( 1 2 2 1 ) x= ( 1 2 ) begin{pmatrix}1\\\\2end{pmatrix} ( 1 2 ) 我们给x左乘A实际

2024年02月04日
浏览(50)
线性代数（8）：特征值、特征向量和相似矩阵

有矩阵 A 为 n 阶矩阵，Ax = λx （ λ 为一个实数，x为 n 维非零列向量），则称 λ 为方阵 A 的特征值， x 为特征向量； 1.2.1 公式求特征值：使 | A - λE | = 0，其解的 λ 值即为矩阵 A 的特征值；求特征向量：使 ( A - λE )x = 0,设 x 为与 A 具有

2024年02月11日
浏览(41)
NumPy之矩阵、向量、线性代数等的操作

在NumPy中，矩阵可以看作是一个二维数组，其中每个元素都可以通过行列坐标来定位。它表示为一个m×n的矩形网格，其中m表示矩阵的行数，n表示矩阵的列数。在计算机科学中，矩阵通常用数字或符号表示，并且可以进行加、减、乘等运算。一个 M X N 的矩阵是一个由 M 行（

2024年02月02日
浏览(32)
线性代数（魏福义）——第二章：矩阵及其向量特征

矩阵是一个矩形数表，它是研究线性方程组、向量及其变换的重要工具在数学中，矩阵是一个按照长方形排列的复数或实数集合，它是将一组有序的数据视为“ 整体量 ”进行表述和运算，从而使问题的表述更加简洁。 2.1.1 矩阵由 m × n 个数aij排成的 m行n列的数表

2024年02月04日
浏览(34)
机器学习——线性代数中矩阵和向量的基本介绍

矩阵的基本概念（这里不多说，应该都知道）而向量就是一个特殊的矩阵，即向量只有一列，是个n*1的矩阵注：一般矩阵用大写字母表示，向量用小写字母表示先从简单开始，即一个矩阵和一个向量相乘的运算矩阵相乘的结果的维度为 m*k 矩阵乘法满足结合律不满足交换律

2024年02月21日
浏览(35)