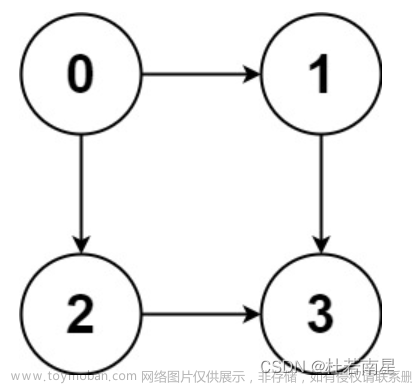
理论:
所有边都经过一次,若欧拉路径,起点终点相同,欧拉回路
有向图欧拉路径:恰好一个out=in+1,一个in=out+1,其余in=out
有向图欧拉回路:所有in=out
无向图欧拉路径:两个点度数奇,其余偶
无向图欧拉回路:全偶
基础练习
P7771 【模板】欧拉路径
P2731 [USACO3.3] 骑马修栅栏 Riding the Fences
P1341 无序字母对
进阶
P3520 [POI2011] SMI-Garbage
题意:n点m条边以及边的目前状态目标状态,若干辆垃圾车跑欧拉回路,每次垃圾车经过改变路的状态
给出需要跑多少次欧拉回路和每次欧拉回路的路径才能所有边实现目标
思路:无向图欧拉回路拆环,
欧拉回路边只经过一次,于是当前状态与目标状态相同的边不用管
变成ol回路拆环问题,考虑在入栈的时候检查该元素是否在栈中,若在,表示成环。
由于常见的求欧拉路的程序给出的结尾都不是开头点,所以在dfs调用后栈里面还剩下一个环,输出即可。文章来源:https://www.toymoban.com/news/detail-744276.html
#include<iostream>
#include<algorithm>
#include<map>
#include<set>
#include<queue>
#include<cstring>
#include<math.h>
#include<map>
#include<vector>
#include<stack>
#define endl '\n'
#define ios ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr)
#define ms(x,y) memset(x,y,sizeof x);
#define YES cout<<"YES"<<'\n';
#define NO cout<<"NO"<<'\n';
#define fr(i,z,n) for(int i = z;i <= n; i++)
#define ufr(i,n,z) for(int i = n;i >= z; i--)
#define fer(i,x) for(int i=e.head[x];~i;i=e.next[i])
typedef long long ll;
const ll N= 1e6 + 10, inf = 1e18;
const ll mod = 1e9 + 7;
using namespace std;
int n, m;
int vist[N]; //标记点
int vis[N<<1]; //标记边
int deg[N],instack[N];
int tot;
stack<int>sta;
vector<int>va[N];
template<size_t size>
struct Road {
int to[size<<1], next[size<<1], head[size<<1], cnt = 1;
ll w[size<<1];
void add(int x, int y, ll ww) {
to[cnt] = y;
w[cnt] = ww;
next[cnt] = head[x];
head[x] = cnt++;
}
void clear(int n) {
for (int i = 0; i <= n; i++) {
head[i] = -1;
}
cnt = 0;
}
};
Road <N> e; // 无向图 * 2
void dfs(int x) {
vist[x] = 1;
fer(i, x) {
int v = e.to[i];
if (!vis[i]) { //边未标记,每条无向边只能走一次
vis[i] = vis[i ^ 1] = 1; //两条有向边组成无向边
e.head[x] = e.next[i]; //下一次直接从nex[i]开始,降低时间复杂度
dfs(v);
if (instack[v]) {
va[tot].push_back(v);
while (sta.top()!=v) {
va[tot].push_back(sta.top());
instack[sta.top()] = 0;
sta.pop();
}
va[tot].push_back(v);
tot++;
}
else {
sta.push(v);
//cout << v << '\n';
instack[v] = 1;
}
}
}
}
void solve() {
scanf("%d %d", &n, &m);
e.clear(n);
fr(i, 1, m) {
int x, y, f, t;
scanf("%d %d %d %d", &x, &y, &f, &t);
if (f ^ t) { //相异,需要经过
e.add(x, y, 0);
e.add(y, x, 0);
deg[x]++;
deg[y]++;
}
}
int flag = 0;
fr(i, 1, n) {
if (deg[i] % 2) { //无向图的欧拉回路应该为全偶
flag = 1;
break;
}
}
if (flag) {
printf("NIE\n");
return;
}
fr(i, 1, n) {
if (!vist[i]) { //点未标记
dfs(i);
if (instack[i]) { //多个环以i为起点,剩余最后一个环
va[tot].push_back(i);
while (!sta.empty()) {
va[tot].push_back(sta.top());
instack[sta.top()] = 0;
sta.pop();
}
tot++;
}
}
}
printf("%d\n", tot);
for (int i = 0; i < tot; i++) {
printf("%d ", va[i].size()-1);
for (auto it : va[i]) {
printf("%d ", it);
}
printf("\n");
}
}
signed main()
{
ios;
int t = 1;
//cin >> t;
while (t--) {
solve();
}
}P3443 [POI2006] LIS-The Postman
题意:给定一个有向图,规定路线从1开始1结束,经过每条边恰好一次,同时给定一些序列
序列在路线中需要连续出现,求满足的路线
x,y<=n<=5e4,m<=2e5
思路:难点在于序列的合并
序列顺序要有边,同时序列的前驱和后继只能有一个,用E存边
用pre,Next记录序列点的前驱后继在E的位置
重新建图(将序列合并),跑欧拉回路,stack入栈起点在在E的位置
最后还要确定每条边都用上文章来源地址https://www.toymoban.com/news/detail-744276.html
#include<iostream>
#include<algorithm>
#include<map>
#include<set>
#include<queue>
#include<cstring>
#include<math.h>
#include<map>
#include<vector>
#include<stack>
#define endl '\n'
#define ios ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr)
#define ms(x,y) memset(x,y,sizeof x);
#define YES cout<<"YES"<<'\n';
#define NO cout<<"NO"<<'\n';
#define fr(i,z,n) for(int i = z;i <= n; i++)
#define ufr(i,n,z) for(int i = n;i >= z; i--)
#define fer(i,x) for(int i=e.head[x];i;i=e.next[i])
typedef long long ll;
const ll N = 1e6 + 10, inf = 1e18;
const ll mod = 1e9 + 7;
using namespace std;
int in[N];
template<size_t size>
struct Road {
int to[size], next[size], head[size], cnt = 1;
ll w[size];
void add(int x, int y, ll ww) {
to[cnt] = y;
w[cnt] = ww;
next[cnt] = head[x];
head[x] = cnt++;
}
void clear(int n) {
for (int i = 0; i <= n; i++) {
head[i] = 0;
}
cnt = 1;
}
};
Road<N>e;
int n, m;
map<int, int>H[N];
pair<int, int>E[N];
int pre[N], Next[N], b[N],vis[N];
stack<int>sta;
bool ans = 0;
void dfs(int x) {
fer(i, x) {
int v = e.to[i];
if (!vis[i]) {
vis[i] = 1;
e.head[x] = e.next[i];
dfs(v);
sta.push(e.w[i]); //入栈起点在E的位置
}
}
}
void solve() {
cin >> n >> m;
fr(i, 1, m) {
int x, y;
cin >> x >> y;
E[i] = make_pair(x, y); //记录边
H[x][y] = i; //记录边在E位置
in[y]++;
in[x]--;
}
fr(i, 1, n) {
if (in[i]) { //有向图的欧拉路径in==out
ans = 1;
}
}
int k;
cin >> k;
fr(i, 1, k) {
int cnt,last;
cin >> cnt;
cin >> last;
for (int j = 1; j < cnt; j++) {
int y;
cin >> y;
if (H[last].find(y) == H[last].end()) { //没有last->y的边
ans = 1;
}
b[j] = H[last][y];
last = y;
}
for (int j = 2; j < cnt;j++) { //处理前驱后继以及边的合并
if (!pre[b[j]]) {
pre[b[j]] = b[j - 1];
}
else if (pre[b[j]] != b[j - 1]) { //因为每条边只能出现一次
ans = 1;
}
if (!Next[b[j-1]]) {
Next[b[j - 1]] = b[j];
}
else if(Next[b[j-1]]!=b[j]) {
ans = 1;
}
}
}
if (ans == 1) {
cout << "NIE" << '\n';
return;
}
int c = 0;
fr(i, 1, m) { //建图
if (!pre[i]) {
++c;
int j;
for (j = i; Next[j]; j = Next[j]) c++;
e.add(E[i].first, E[j].second, i); //i记录起点在E的位置
}
}
if (c < m || !e.head[1]) { //判断联通(c==m)和能否从1开始
cout << "NIE" << '\n';
return;
}
fr(i, 1, n) { //建图后需要再判断
if (in[i]) {
cout << "NIE" << '\n';
return;
}
}
dfs(1); //欧拉回路
fr(i, 1, n) {
if (e.head[i]) { //确定每条边都用上
cout << "NIE" << '\n';
return;
}
}
cout << "TAK" << '\n';
cout << 1 <<'\n';
while (!sta.empty()) {
int j = sta.top();
sta.pop();
while (j) {
cout << E[j].second << '\n';
j = Next[j];
}
}
}
signed main()
{
ios;
int t = 1;
//cin >> t;
while (t--) {
solve();
}
}到了这里,关于图论(欧拉路径)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!