目录
夯实基础--FFT算法
定点运算--verilog实现小数运算
Verilog代码实现
FFT系数 W 的准备
输入数值的初始化
蝶形运算端点处的值
仿真结果展示
总结
夯实基础--FFT算法
FFT是DFT的一种快速算法而不是一种新的变换,他可以在数量级的意义上提高运算速度。它主要有两种实现方法:一种是按时间抽取(DIT),另一种是按频域抽取(DIF)。为了方便起见,我们选用基于时间抽取的FFT的算法。
算法原理:先设序列x(n)的点数为N = 2^L(L为正整数
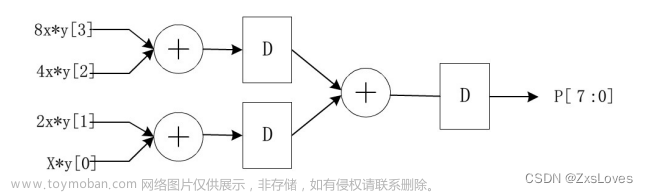
将N=2^L的偶数序列x(n)按n的奇偶将序列分成两组,对两组新的序列。在对N点的序列进行DFT运算的时候按奇偶将序列分开,我们便可根据系数W的可约性得到前N/2的DFT的点的值,根据W的周期性有可以得到后面N/2点的DFT的值。详细请参考数字信号处理,在此就不过多的解释。我们以16点FFT为例,在此粘贴处他的蝶形图

还有一点,FFT的运算为输入倒位序,输出自然顺序或者是输入自然顺序,输出倒位序。这里我们采取输入倒位序,输出自然顺序
(倒位序:将n的值转换成二进制,倒过来重新排序所组成的值)
定点运算--verilog实现小数运算
定点运算,顾名思义,我们在运算的过程中需要确定小数点的位置,让小数点的位置保持不变
实现原理:对于一个数,我们可以把他分成三个部分:符号位,整数部分和小数部分。
若 x 表示一个实际的浮点数,q表示他的Qn 型的定点小数(一个整数)。n表示小数点固定的位置
则 q = x * 2^n ,x = q / 2^n
举例: 计算 2.1 * 2.2 (此处我们选择Q12定点小数)
2.1 * 2^12 = 8601.6 = 8602
2.2 * 2^12 = 9011.2 = 9011
(8602*9011)/2^12 = 18923 (除以12的原因:两数相乘使得小数点后有24位,所以我们需要除以2^12,固定小数点)
最终结果 = 18923/ 2^12 = 4.619873 而2.1*2.2 = 4.62
我们可以知道结果相差不大,故我们可以用这种方法实现小数运算
注:当我们用verilog实现的时候我们需要注意格式,在进行负数运算的时候我们是以二进制补码的形式储存的,而 数值大小的运算我们用原码进行运算,在计算过程中注意符号
Verilog代码实现
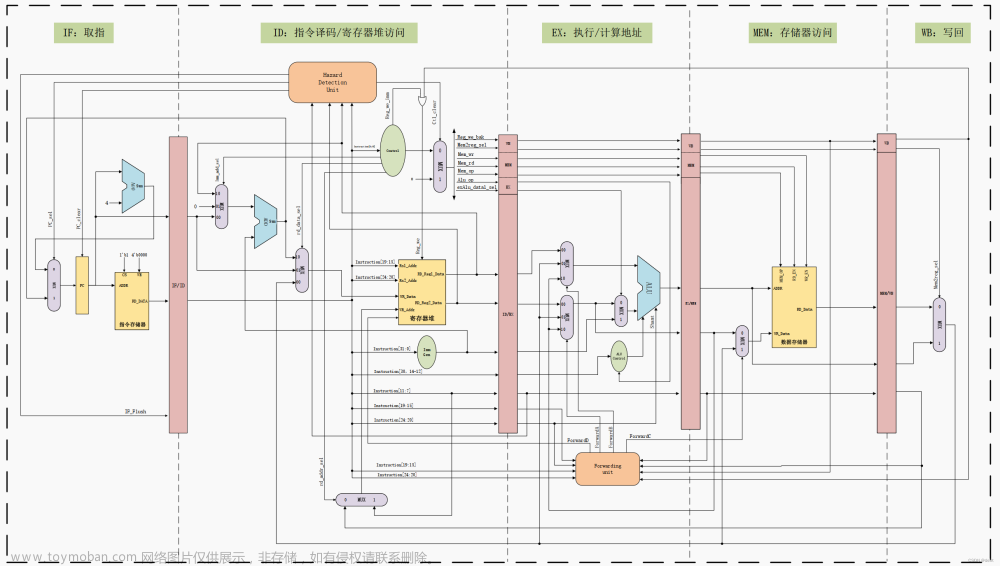
根据上面的fft16的蝶形图,我们可以选择使用四级流水线进行实现
FFT系数 W 的准备
W的值的运算我们可以用过matlab运算得到,此处我直接把需要用到的W的值给出 W(下标,上标)
W(4,1)=W(8,2)=W(16,4)=-j ;W(8,1)=W(16,2)=0.7071-0.7071j
W(8,3)=W(16,6)=-0.7071-0.7071j ; W(16,3)=0.3827-0.9239;W(16,5)=-0.3827-0.9239 ;
W(16,7)=-0.9239-0.3827 ; W(16,1)=0.9239-0.3827
我们可以看出主要小数就是0.9239 ;0.3837 ; 0.7071这三个数,此处我们采取Q12的定点方法进行verilog定义
wire [WIDTH-1:0] coe_dly1_p ;
wire [WIDTH-1:0] coe_dly1_n ;
wire [WIDTH-1:0] coe_dly2_p ;
wire [WIDTH-1:0] coe_dly2_n ;
wire [WIDTH-1:0] coe_dly3_p ;
wire [WIDTH-1:0] coe_dly3_n ;
//0.7071
assign coe_dly1_p = 2896;
assign coe_dly1_n = 2896 ;
//0.3827
assign coe_dly2_p = 1568;
assign coe_dly2_n = 1568 ;
//0.9239
assign coe_dly3_p = 3874;
assign coe_dly3_n = 3874 ; 此处后缀 _p 和 _n 来区别正负,我们需要用原码来进行运算,所以不可以直接给符号(否则以补码形式储存得到错误的结果)
输入数值的初始化
由于我们选定的是Q12定点运算,故我们需要对输入的数据进行扩大,方便后续的运算(再次提醒:数据的操作用原码!!)
assign fft0_re_inst=(fft0_re[WIDTH-1]==1'b1)?({1'b1,~((~fft0_re[WIDTH-2:0]+1'b1)<<12)+1'b1}):({1'b0,fft0_re[WIDTH-2:0]<<12});
assign fft0_im_inst=(fft0_im[WIDTH-1]==1'b1)?({1'b1,~((~fft0_im[WIDTH-2:0]+1'b1)<<12)+1'b1}):({1'b0,fft0_im[WIDTH-2:0]<<12});
assign fft1_re_inst=(fft0_re[WIDTH-1]==1'b1)?({1'b1,~((~fft1_re[WIDTH-2:0]+1'b1)<<12)+1'b1}):({1'b0,fft1_re[WIDTH-2:0]<<12});
assign fft1_im_inst=(fft0_im[WIDTH-1]==1'b1)?({1'b1,~((~fft1_im[WIDTH-2:0]+1'b1)<<12)+1'b1}):({1'b0,fft1_im[WIDTH-2:0]<<12});
assign fft2_re_inst=(fft0_re[WIDTH-1]==1'b1)?({1'b1,~((~fft2_re[WIDTH-2:0]+1'b1)<<12)+1'b1}):({1'b0,fft2_re[WIDTH-2:0]<<12});
assign fft2_im_inst=(fft0_im[WIDTH-1]==1'b1)?({1'b1,~((~fft2_im[WIDTH-2:0]+1'b1)<<12)+1'b1}):({1'b0,fft2_im[WIDTH-2:0]<<12});
assign fft3_re_inst=(fft0_re[WIDTH-1]==1'b1)?({1'b1,~((~fft3_re[WIDTH-2:0]+1'b1)<<12)+1'b1}):({1'b0,fft3_re[WIDTH-2:0]<<12});蝶形运算端点处的值
为了缓解运算的复杂度,避免时序的问题,通过打拍的方式将每个端点需要进行处理的值在打拍过程中实现,这样就缓解了组合电路的压力。第一级和第二级端点处的处理比较简单,在这里不做过多的解释,我们重点讲解下第三级和第四级的端点处的处理
我们先用相关的原码计算得到结果值(主要是两数相乘,注意小数点的处理),然后根据‘同号得正,异号得负’的原理来处理得到最终的结果(因为我们是以补码形式储存的),在这里粘贴部分代码供参考:
//得到原码
assign fft5_re_dly2_temp = (fft5_re_dly2[WIDTH-1]==1'b1)?(~fft5_re_dly2+1'b1):fft5_re_dly2;
assign fft5_im_dly2_temp = (fft5_im_dly2[WIDTH-1]==1'b1)?(~fft5_im_dly2+1'b1):fft5_im_dly2;
assign fft7_re_dly2_temp = (fft7_re_dly2[WIDTH-1]==1'b1)?(~fft7_re_dly2+1'b1):fft7_re_dly2;
assign fft7_im_dly2_temp = (fft7_im_dly2[WIDTH-1]==1'b1)?(~fft7_im_dly2+1'b1):fft7_im_dly2;
//得到端点处的相关系数的原码的值
always@(posedge sys_clk or negedge sys_rst_n)
begin
if(~sys_rst_n)
begin
fft5_fft1_re_dly1 <=0;
fft5_fft1_re_dly2 <=0;
fft5_fft1_im_dly1 <=0;
fft5_fft1_im_dly2 <=0;
fft3_fft7_re_dly1 <=0;
fft3_fft7_re_dly2 <=0;
fft3_fft7_im_dly1 <=0;
fft3_fft7_im_dly2 <=0;
end
else
begin
fft5_fft1_re_dly1 <=(fft5_re_dly2_temp*coe_dly1_p )>>12;
fft5_fft1_re_dly2 <=(fft5_im_dly2_temp*coe_dly1_n )>>12;
fft5_fft1_im_dly1 <=(fft5_re_dly2_temp*coe_dly1_n )>>12;
fft5_fft1_im_dly2 <=(fft5_im_dly2_temp*coe_dly1_p )>>12;
fft3_fft7_re_dly1 <=(fft7_re_dly2_temp*coe_dly1_n )>>12;
fft3_fft7_re_dly2 <=(fft7_im_dly2_temp*coe_dly1_n )>>12;
fft3_fft7_im_dly1 <=(fft7_im_dly2_temp*coe_dly1_n )>>12;
fft3_fft7_im_dly2 <=(fft7_re_dly2_temp*coe_dly1_n )>>12;
end
end
end
//转换成补码形式储存下来并进行后续的运算
//最高位为1表示负数
assign fft5_fft1_re_dly1_wn = (fft5_re_dly2_dly[WIDTH-1]==1'b1)?(~fft5_fft1_re_dly1+1'b1):fft5_fft1_re_dly1;
assign fft5_fft1_re_dly2_wn = (fft5_im_dly2_dly[WIDTH-1]==1'b1)?fft5_fft1_re_dly2:(~fft5_fft1_re_dly2+1'b1);
assign fft5_fft1_im_dly1_wn = (fft5_re_dly2_dly[WIDTH-1]==1'b0)?(~fft5_fft1_re_dly1+1'b1):fft5_fft1_re_dly1;
assign fft5_fft1_im_dly2_wn = (fft5_im_dly2_dly[WIDTH-1]==1'b0)?fft5_fft1_re_dly2:(~fft5_fft1_re_dly2+1'b1);
assign fft3_fft7_re_dly1_wn = (fft7_re_dly2_dly[WIDTH-1]==1'b1)?fft3_fft7_re_dly1:(~fft3_fft7_re_dly1+1'b1);
assign fft3_fft7_re_dly2_wn = (fft7_im_dly2_dly[WIDTH-1]==1'b1)?fft3_fft7_re_dly2:(~fft3_fft7_re_dly2+1'b1);
assign fft3_fft7_im_dly1_wn = (fft7_im_dly2_dly[WIDTH-1]==1'b1)?fft3_fft7_im_dly1:(~fft3_fft7_im_dly1+1'b1);
assign fft3_fft7_im_dly2_wn = (fft7_re_dly2_dly[WIDTH-1]==1'b1)?fft3_fft7_im_dly2:(~fft3_fft7_im_dly2+1'b1);第三级和第四级处理方法类似,理解了一个另一个也很容易理解
仿真结果展示
tb代码
initial
begin
clk = 1'b0 ;
rst = 1'b0 ;
#20
rst = 1'b1 ;
end
always #10 clk = ~clk ;
fft16
#(
.WIDTH ('d32)
)
fft16_inst
(
.sys_clk(clk),
.sys_rst_n(rst),
.fft0_re('d1),
.fft1_re('d2),
.fft2_re('d2),
.fft3_re('d1),
.fft4_re('d2),
.fft5_re('d1),
.fft6_re('d1),
.fft7_re('d2),
.fft8_re('d2),
.fft9_re('d1),
.fft10_re('d1),
.fft11_re('d2),
.fft12_re('d1),
.fft13_re('d1),
.fft14_re('d1),
.fft15_re('d2),
.fft0_im('d0),
.fft1_im('d0),
.fft2_im('d0),
.fft3_im('d0),
.fft4_im('d0),
.fft5_im('d0),
.fft6_im('d0),
.fft7_im('d0),
.fft8_im('d0),
.fft9_im('d0),
.fft10_im('d0),
.fft11_im('d0),
.fft12_im('d0),
.fft13_im('d0),
.fft14_im('d0),
.fft15_im('d0),
//output
.fft0_re_out(fft0_re_out),
.fft1_re_out(fft1_re_out),
.fft2_re_out(fft2_re_out),
.fft3_re_out(fft3_re_out),
.fft4_re_out(fft4_re_out),
.fft5_re_out(fft5_re_out),
.fft6_re_out(fft6_re_out),
.fft7_re_out(fft7_re_out),
.fft8_re_out(fft8_re_out),
.fft9_re_out(fft9_re_out),
.fft10_re_out(fft10_re_out),
.fft11_re_out(fft11_re_out),
.fft12_re_out(fft12_re_out),
.fft13_re_out(fft13_re_out),
.fft14_re_out(fft14_re_out),
.fft15_re_out(fft15_re_out),
.fft0_im_out(fft0_im_out),
.fft1_im_out(fft1_im_out),
.fft2_im_out(fft2_im_out),
.fft3_im_out(fft3_im_out),
.fft4_im_out(fft4_im_out),
.fft5_im_out(fft5_im_out),
.fft6_im_out(fft6_im_out),
.fft7_im_out(fft7_im_out),
.fft8_im_out(fft8_im_out),
.fft9_im_out(fft9_im_out),
.fft10_im_out(fft10_im_out),
.fft11_im_out(fft11_im_out),
.fft12_im_out(fft12_im_out),
.fft13_im_out(fft13_im_out),
.fft14_im_out(fft14_im_out),
.fft15_im_out(fft15_im_out)
);
结果这里通过我手算的结果和仿真的结果进行比较验算



( 由于个人原因我只算了前8个点的值,不过由于前8个点和后8个点的只有+ 和 - 的区别,所用的数值的一样的,所以前8个对了,后面的也就没什么问题。)
通过比较,我们可以发现他们的误差还是比较小的,这是由于modelsim仿真的时候他遇到小数采取的方式不是四舍五入,而是直接舍掉。
还有最重要的一点:现在仿真得到的结果不是最终的值,他存储的结果是Q12型小数补码的形式,如果要得到最终的结果,我们需要手动对结果进行处理。切记!!!文章来源:https://www.toymoban.com/news/detail-744365.html
总结
本人第一次写csdn,其中如果有写的不正确或者不恰当的地方还请多多批评指正,在下不胜感激。文章来源地址https://www.toymoban.com/news/detail-744365.html
到了这里,关于基于verilog的四级流水线实现并行fft16(可计算小数和负数)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!