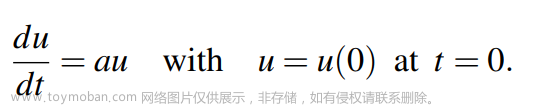伯努利方程
伯努利方程的标准形式:

伯努利方程解法:
方程两边同时除以y的n次,

做变量替换y->z:

转换为线性微分方程:

最后换回原来的变量即可得到伯努利方程。
一阶线性微分方程
一阶线性微分方程的标准形式:

当Q(x)=0,为齐次方程;当Q(x)≠0,为非齐次方程。
求解一阶线性齐次微分方程

求解一阶线性非齐次微分方程

矩阵的一阶线性微分方程
已知如下矩阵,求解一阶线性微分方程

求解一阶线性齐次微分方程
矩阵微分方程表示为

求矩阵微分方程的解

得到 x(t)如下,c 为常数向量

求解一阶线性非齐次微分方程
矩阵微分方程表示为

求矩阵微分方程的解

对微分方程两边在[t0,t]上积分文章来源:https://www.toymoban.com/news/detail-744563.html

得到 x(t)如下文章来源地址https://www.toymoban.com/news/detail-744563.html

到了这里,关于(矩阵)一阶微分方程和伯努利方程的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!