图的存储结构-十字链表-Toy模板网

这篇具有很好参考价值的文章主要介绍了图的存储结构-十字链表。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

图的存储结构-十字链表

十字链表（Orthogonal List）是有向图的一种链式存储结构。可以看成是将有向图的邻接表和逆邻接表结合起来得到的一种链表。在十字链表中，对应于有向图中每一条弧有一个结点，对应于每个顶点也有一个结点。

十字链表的结构

顶点结点

十字链表,数据结构,链表,数据结构,算法

typedef string InfoType ;
typedef string VertexType;

typedef struct VexNode{
    VertexType data; //顶点的数据域
    ArcBox *firstIn; //指向该顶点的第一条入弧
    ArcBox *firstOut; //指向该顶点的第一条出弧
}VexNode;

弧结点

十字链表,数据结构,链表,数据结构,算法

typedef struct ArcBox{
    int tailVex; //该弧的尾顶点的位置
    int headVex; //该弧的头顶点的位置
    struct ArcBox * hLink; //弧头相同的弧的链域
    static ArcBox * tLink; //弧尾相同的弧的链域
    InfoType info; //弧的相关信息
}ArcBox;

十字链表结点：

#define MAX_VERTEX_BUM 20
typedef struct {
    VexNode xList[MAX_VERTEX_BUM]; //表头向量
    int vexNum; //图的顶点个数
    int arcNum; //图的边数
}OLGraph;

有向图十字链表

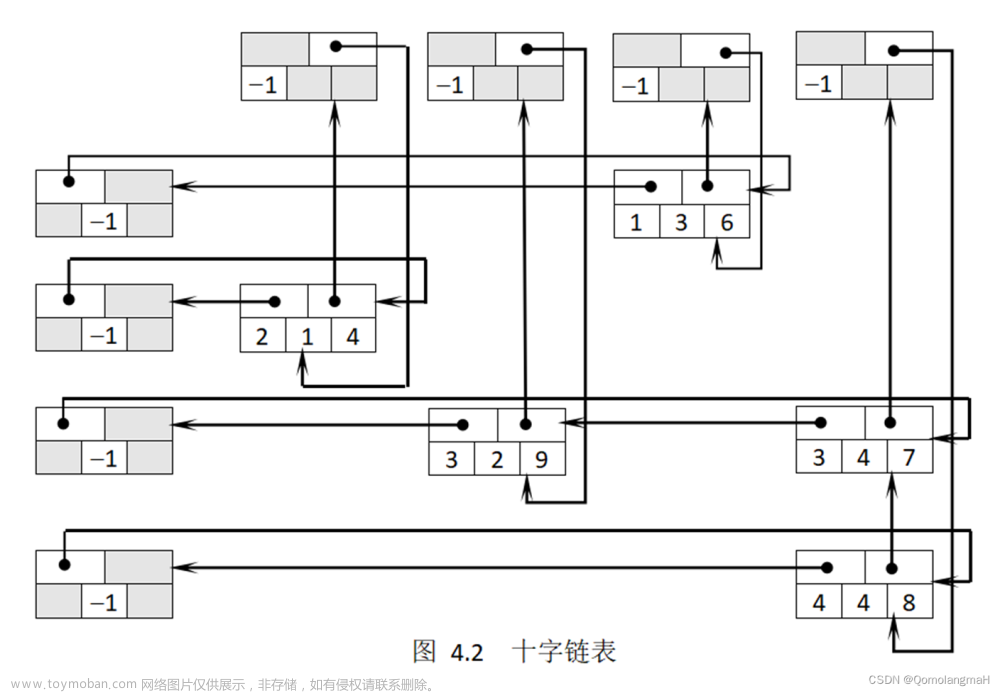
在弧结点中有5个域：其中尾域（tailvex）和头域（headvex）分别指示弧尾和弧头这两个顶点在图中的位置，链域hlink指向弧头相同的下一条弧，而链域tlink指向弧尾相同的下一条弧，info域指向该弧的相关信息。弧头相同的弧在同一链表上，弧尾相同的弧也在同一链表上。
它们的头结点即为顶点结点，它由3个域组成：其中data域存储和顶点相关的信息，如顶点的名称等；firstIn和firstOut为两个链域，分别指向以该顶点为弧头或弧尾的第一条弧结点。如下图：
十字链表,数据结构,链表,数据结构,算法
若将有向图的邻接矩阵看成稀疏矩阵的话，则十字链表也可以看成是邻接矩阵的链式存储结构，在图的十字链表中，弧结点所在的链表非循环链表，结点之间相对位置自然形成，不一定按顶点序号有序，表头结点即顶点，它们之间不是链接，而是顺序存储。

使用十字链表法创建一个有向图

OLGraph CreateOLG() {
    OLGraph G;
    cout << "输入顶点的总数，边的总数 G(V,E)" << endl;
    cin >> G.vexNum >> G.arcNum;  //输入总顶点数，总边数

    for (int vi = 0; vi < G.vexNum; ++vi) {
        cout << "输入顶点" << vi << "的值：" << endl;
        cin >> G.xList[vi].data;    //输入顶点的值
        G.xList[vi].firstIn = NULL; //初始化入弧表
        G.xList[vi].firstOut = NULL; //初始化出弧表
    }

    int i = -1, j = -1;
    for (int k = 0; k < G.arcNum; ++k) {
        VertexType v1, v2;
        cout << "请输入边的值 (vi,vj) " << endl;
        cin >> v1 >> v2; //输入一条边依附的两个顶点
        i = LocateVex(G, v1); //获得v1 在G.xList[]中的位置
        j = LocateVex(G, v2); //获得v2 在G.xList[]中的位置

        ArcBox *p1 = new ArcBox;  //生成一个新的边 *p1
        p1->tailVex = i; //弧尾的顶点位置
        p1->headVex = j; //弧头的顶点位置
        p1->tLink = G.xList[i].firstOut;
        p1->hLink = G.xList[j].firstIn;
        G.xList[i].firstOut = p1;
        G.xList[j].firstIn = p1;

    }
    return G;
}
/**
 * 若图G中存在顶点u，则返回该顶点在图中的位置；否则返回其它信息；
 */
int LocateVex(OLGraph G, VertexType u) {
    int i;
    for (i = 0; i < G.vexNum; ++i)
        if (u == G.xList[i].data)
            return i;
    return -1;
}

过程图解

1.初始化图G（V,E）;

		cin >> G.xList[vi].data;    //输入顶点的值
        G.xList[vi].firstIn = NULL; //初始化入弧表
        G.xList[vi].firstOut = NULL; //初始化出弧表

十字链表,数据结构,链表,数据结构,算法
2.创建一个边结点

 		ArcBox *p1 = new ArcBox;  //生成一个新的边 *p1
        p1->tailVex = i; //弧尾的顶点位置
        p1->headVex = j; //弧头的顶点位置

十字链表,数据结构,链表,数据结构,算法
3.将边结点加入十字链表
先将边结点的插入弧尾相同的链表表头；

 		p1->tLink = G.xList[i].firstOut;

十字链表,数据结构,链表,数据结构,算法
在把边结点的插入弧头相同的链表表头；

		p1->hLink = G.xList[j].firstIn;

十字链表,数据结构,链表,数据结构,算法
最后让弧尾顶点的第一条出弧、弧头顶点的第一条入弧，指向新加入的边界点；

        G.xList[i].firstOut = p1;
        G.xList[j].firstIn = p1;

十字链表,数据结构,链表,数据结构,算法
4.继续加入先得边结点

文章来源地址https://www.toymoban.com/news/detail-744750.html

到了这里，关于图的存储结构-十字链表的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

图的存储结构-十字链表