时序分解 | Matlab实现NGO-VMD北方苍鹰算法优化变分模态分解时间序列信号分解-Toy模板网

这篇具有很好参考价值的文章主要介绍了时序分解 | Matlab实现NGO-VMD北方苍鹰算法优化变分模态分解时间序列信号分解。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

时序分解 | Matlab实现NGO-VMD北方苍鹰算法优化变分模态分解时间序列信号分解

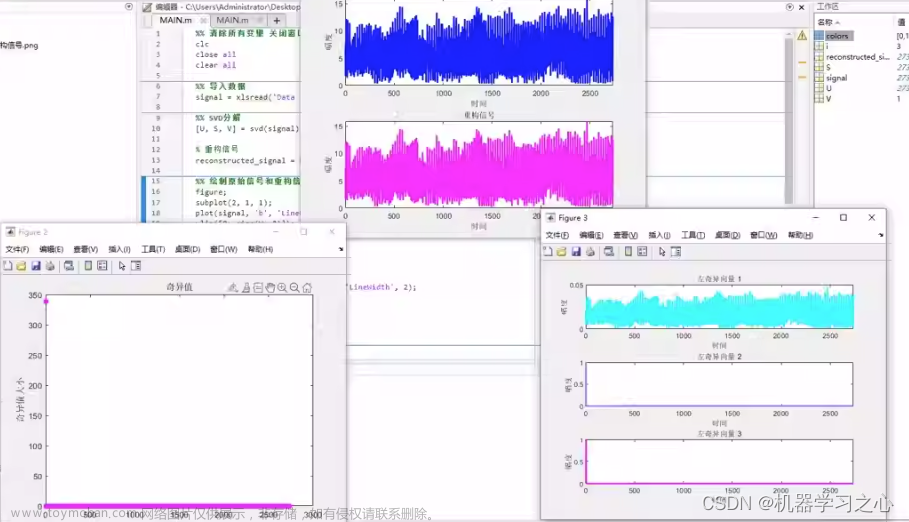
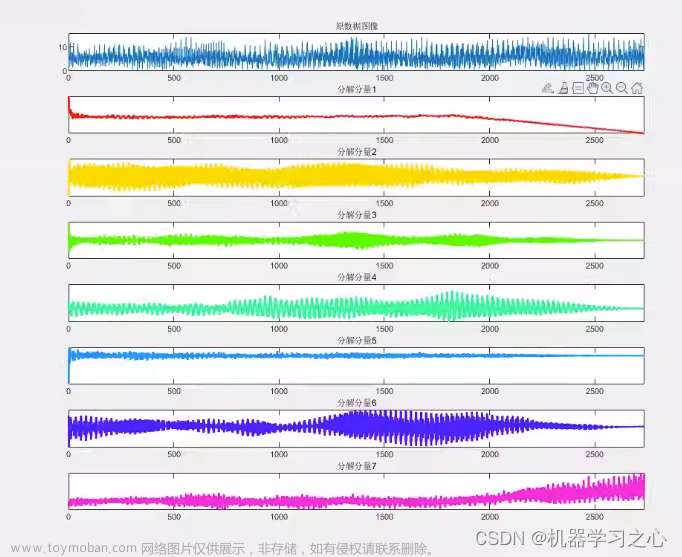
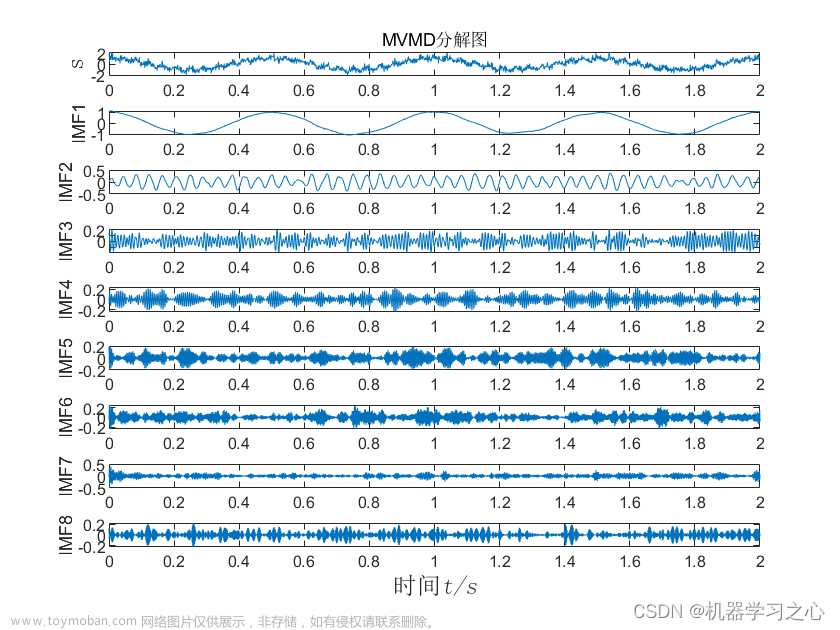
效果一览

时序分解 | Matlab实现NGO-VMD北方苍鹰算法优化变分模态分解时间序列信号分解,时序分解,NGO-VMD,北方苍鹰算法优化,变分模态分解,时间序列信号分解

基本介绍

北方苍鹰算法NGO优化VMD，对其分解层数，惩罚因子数做优化，利用NGO优化算法确定其最佳参数，适应度函数为样本熵。
NGO-VMD北方苍鹰算法NGO优化VMD变分模态分解可直接运行分解效果好适合作为创新点（Matlab完整源码和数据)
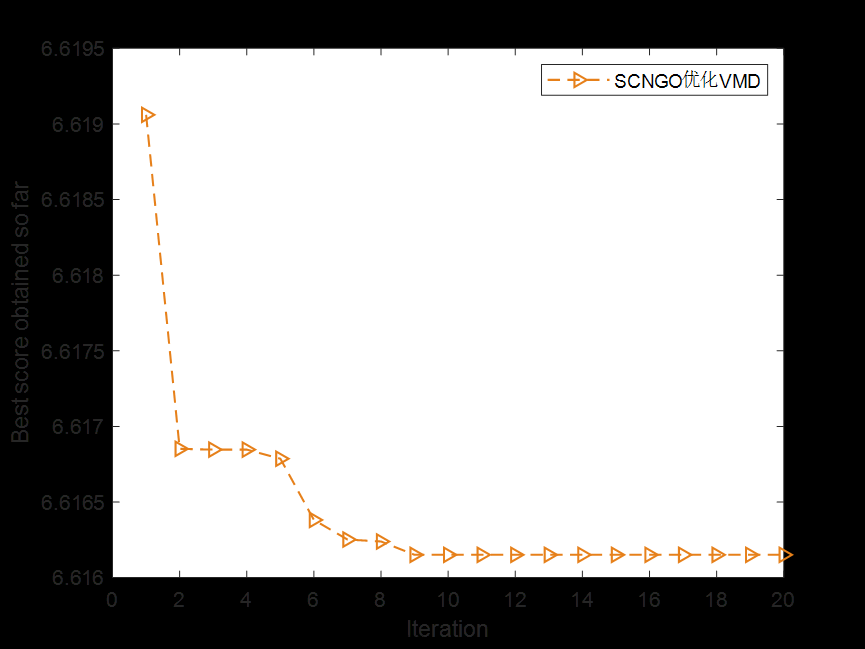
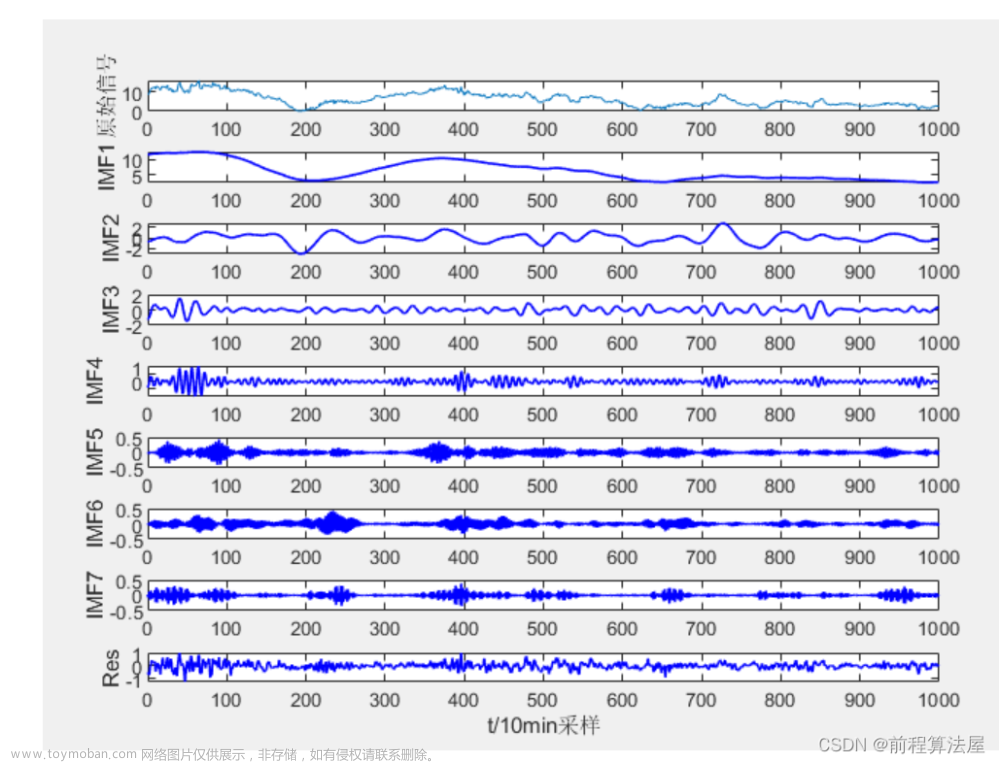
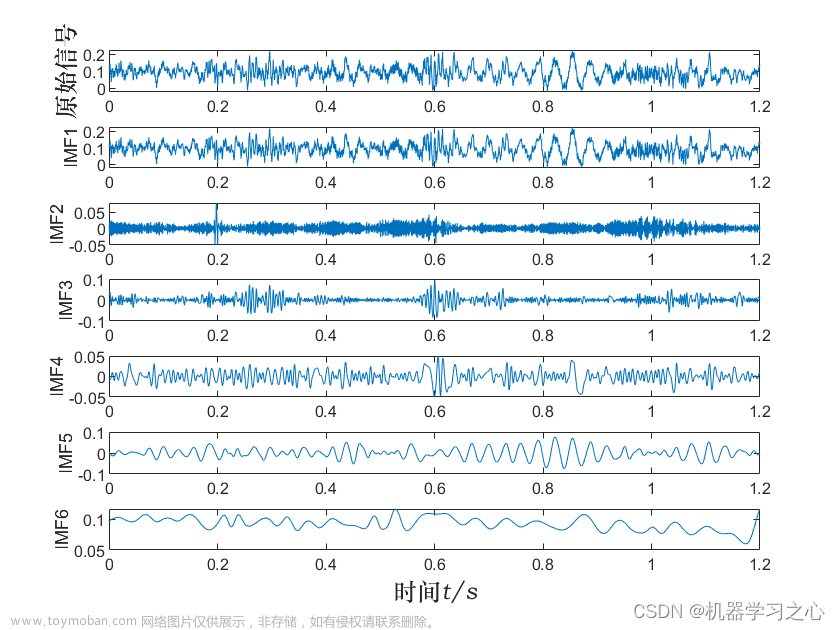
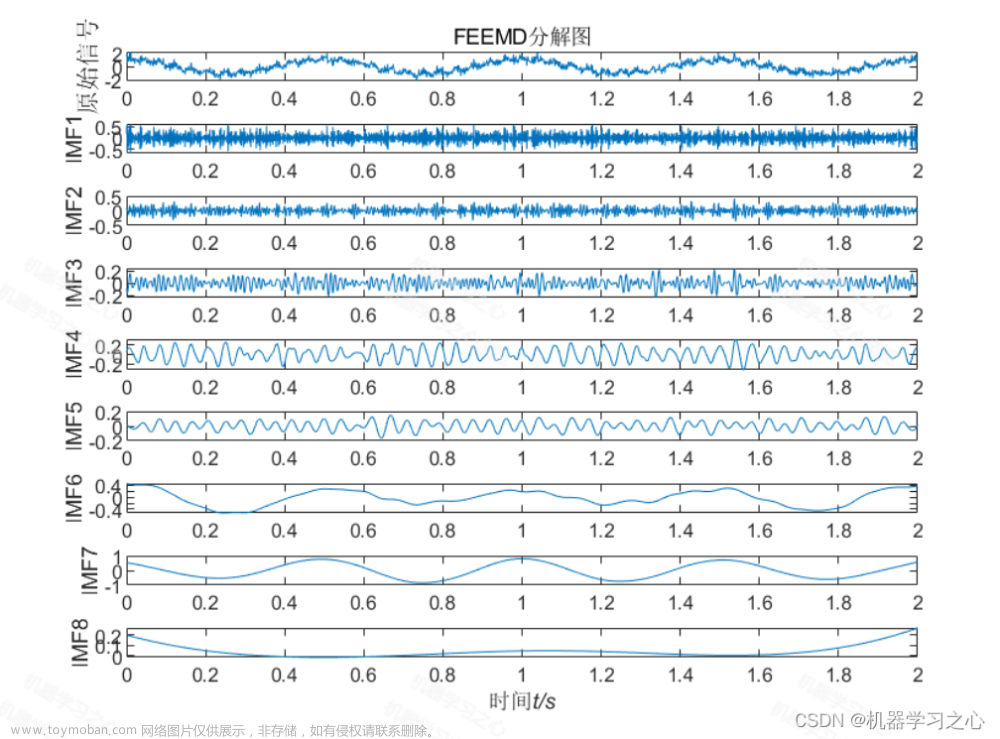
1.利用北方苍鹰算法算法优化vmd中的参数k、a，分解效果好，包含边际谱、频率图、收敛曲线等图，满足您的需求，使用者较少，适合作为创新点。
2.包含VMD超参数优化迭代过程图，凸显每次迭代过程的变化。
3.北方苍鹰算法(NGO)是一种新型的群智能优化算法，具有收敛速度快、寻优能力强等优点。
4.数据为excel数据，方便替换，运行主程序main即可，可直接运行matlab程序。

程序设计

完整源码和数据获取方式私信博主回复：Matlab实现NGO-VMD北方苍鹰算法优化变分模态分解时间序列信号分解。


fobj = @(x) fun(x,f,tau, DC, init, tol);
[~,Target_pos,process] = NGO(pop,Max_iteration,lb,ub,dim,fobj);%优化函数 求K Alpha 熵值
%_________________________________________________________________________%
% NGO 北方苍鹰优化算法                %
%_________________________________________________________________________%
function [Score,Best_pos,NGO_curve,result]=NGO(Search_Agents,Max_iterations,Lowerbound,Upperbound,dimensions,fobj)
tic

disp('PLEASE WAIT, The program is running.')

Lowerbound=ones(1,dimensions).*(Lowerbound);                              % 变量的下限
Upperbound=ones(1,dimensions).*(Upperbound);                              % 变量的上限


X=[];
X_new=[];
fit=[];
fit_new=[];
NGO_curve=zeros(1,Max_iterations);

%%
for i=1:dimensions
    X(:,i) = Lowerbound(i)+rand(Search_Agents,1).*(Upperbound(i) -Lowerbound(i));              % 初始种群
end
for i =1:Search_Agents
    %L=X(i,:);
    fit(i)=fobj(X(i,:));                    % 初始群体适应度评估  )
end

disp('打印迭代次数');

参考资料

[1] https://blog.csdn.net/kjm13182345320/article/details/129215161
[2] https://blog.csdn.net/kjm13182345320/article/details/128105718文章来源地址https://www.toymoban.com/news/detail-745078.html

到了这里，关于时序分解 | Matlab实现NGO-VMD北方苍鹰算法优化变分模态分解时间序列信号分解的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！