图的最短路径

最短路径分为两种:
(1)单源路径:从某顶点出发,到其他全部顶点的最短路径
(2)顶点间的最短路径:任意两个顶点之间的最短路径
最短路径的结果主要有两个方面:
(1)顶点之间最短路径的长度
(2)从源顶点到目标顶点的路径
BFS
只有边权为 1 时才能用BFS求最短路。
为什么BFS能求边权为1的图的最短路呢?
其实可以把整个遍历路径看成一棵树
我们会看到是一层一层遍历的
也就是说 只要这个节点被访问到了,那么根节点到这个节点的最短路径就已经确定了


可以看到 2到1的最短路径就是1到6也是1
以此类推,2到8的最短路径就是3

从2出发,计算2到8的最短路径
第一步:初始化

d[i]=∞
path[i]=-1
d[2]=0 //2到自身的路径长度为0
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|
| d[] | inf | 0 | inf | inf | inf | inf | inf | inf |
| path[] | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|
| visited | F | T | F | F | F | F | F | F |
| queue | 2 |
|---|
第二步:从2出发,找到邻接点1、6
2出队 1、6进队
| queue | 1 | 6 |
|---|

path存的是当前节点的父节点,所以path[1] = 2 path[6] = 2
d[1] = d[2]+1 = 1
d[6] = d[2]+1 = 1
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|
| d[] | 1 | 0 | inf | inf | inf | 1 | inf | inf |
| path[] | 2 | -1 | -1 | -1 | -1 | 2 | -1 | -1 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|
| visited | T | T | F | F | F | T | F | F |
第三步:节点1出队,找到邻接节点5
1出队 5进队
| queue | 6 | 5 |
|---|
d[5] = d[1]+1 = 2
path[5] = 1

| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|
| d[] | 1 | 0 | inf | inf | 2 | 1 | inf | inf |
| path[] | 2 | -1 | -1 | -1 | 1 | 2 | -1 | -1 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|
| visited | T | T | F | F | T | T | F | F |
第四步:节点6出队,找到邻接节点2、3、7
6出队 3、7进队,2访问过,忽略
| queue | 5 | 3 | 7 |
|---|
path[3] = 6
path[7] = 6
d[3] = d[7] = d[6]+1 = 2

| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|
| d[] | 1 | 0 | 2 | inf | 2 | 1 | 2 | inf |
| path[] | 2 | -1 | 6 | -1 | 1 | 2 | 6 | -1 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|
| visited | T | T | T | F | T | T | T | F |
第五步:节点5出队,没有邻接节点
5出队
| queue | 3 | 7 |
|---|
第六步:节点3出队,找到邻接节点6、4、7
3出队,4入队,6、7已经被访问过了 忽略
| queue | 7 | 4 |
|---|
d[4] = d[3]+1 = 2+1 = 3
path[4] = 3

| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|
| d[] | 1 | 0 | 2 | 3 | 2 | 1 | 2 | inf |
| path[] | 2 | -1 | 6 | 3 | 1 | 2 | 6 | -1 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|
| visited | T | T | T | T | T | T | T | F |
第七步:节点7出队,找到邻接节点3、4、8
7出队,8入队,3、4已经被访问过了 忽略
| queue | 4 | 8 |
|---|
d[8] = d[7]+1 = 2+1 = 3
path[8] = 7

| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|
| d[] | 1 | 0 | 2 | 3 | 2 | 1 | 2 | 3 |
| path[] | 2 | -1 | 6 | 3 | 1 | 2 | 6 | 7 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|
| visited | T | T | T | T | T | T | T | T |
第七步:节点4出队,找到邻接节点3、7、8
3、7、8已经被访问过了 忽略
| queue | 8 |
|---|
第八步:节点8出队,找到邻接节点4、7
4、7、已经被访问过了 忽略
| queue |
|---|
至此,广搜结束,输出结果d[8] = 2
代码实现
const bfs = (graph,node)=>{
const n = Object.keys(graph).length
const visited = new Array(n+1).fill(false)
const max = Number.MAX_SAFE_INTEGER
const d = new Array(n).fill(max)
const path = new Array(n+1).fill(-1)
d[node] = 0
visited[node] = true
const queqe = [node]
// 开始深搜
while(queqe.length){
const newnode = queqe.shift()
const v = graph[newnode]
v&&v.map(item=>{
// 这个节点没有访问过
if(!visited[item]){
path[item] = newnode
d[item] = d[newnode]+1
visited[item] = true
queqe.push(item)
}
})
}
// 输出路径
const rspath = [8]
while(rspath[0]===node){
rspath.unshift(path[rspath[0]])
}
console.log(rspath) // 2 6 7 8
return d[8] //3
}
const graph = {
1:[2,5],
2:[1,6],
3:[6,7,4],
4:[3,7,8],
5:[1],
6:[2,3,7],
7:[6,3,8],
8:[7,4],
}
console.log(bfs(graph,2))
迪杰斯特拉 dijkstra
dijkstra求单源最短路的,思想是贪心,每次都取最小值去更新下一个节点
算法过程:
1)dist[]存储第i个节点到家的距离,visited[i]=true 代表第i个点是否已经遍历过。
2)遍历所有visited[i] == false的点,找出dist[i]最小的点 k。
3)遍历与k相连的点j,用 min(dist[j], dist[k] + edge[k][j])来更新 dist[j]。
4)将visited[k] = true;
5) 如果还存在点,返回2)
第一步:初始化
visited[i] = false
dist[i] = inf
path[i] = -1
dist[0]=0

| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|
| visited[] | F | F | F | F | F | F | F | F |
| dist[] | 0 | inf | inf | inf | inf | inf | inf | inf |
| path[] | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 |
第二步:从dist数组中找到未被访问的最小值的节点,然后更新相邻节点
dist数组中最小值0,对应节点0
节点0相邻的节点有v1 v2 v3
所以 path[1] = path[2] = path[3] = 0
dist[1] = dist[0]+4=0+4=4
dist[2] = dist[0]+3=0+3=3
dist[3] = dist[0]+10=0+10=10
更新完毕 标志节点已访问
visited[0] = true
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|
| visited[] | T | F | F | F | F | F | F | F |
| dist[] | 0 | 4 | 3 | 10 | inf | inf | inf | inf |
| path[] | -1 | 0 | 0 | 0 | -1 | -1 | -1 | -1 |
第三步:继续第二步操作,找到节点v2
节点2相邻的节点有v3 v6
dist[6] = min(dist[2]+12,dist[6])=dist[2]+12=3+12 = 15
dist[3] = min(dist[2]+5,dist[3])=dist[2]+5=3+5 = 8
path[6] = path[3] = 2
更新完毕 标志节点已访问
visited[2] = true

| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|
| visited[] | T | F | T | F | F | F | F | F |
| dist[] | 0 | 4 | 3 | 8 | inf | inf | 15 | inf |
| path[] | -1 | 0 | 0 | 2 | -1 | -1 | 2 | -1 |
第四步:继续第二步操作,找到节点v1
节点1相邻的节点有v3 v4
dist[4] = min(dist[1]+8,dist[4])=dist[1]+8=4+8 = 12
dist[3] = min(dist[1]+3,dist[3])=dist[1]+3=4+3 = 7
path[4] = path[3] = 1
更新完毕 标志节点已访问
visited[1] = true

| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|
| visited[] | T | T | T | F | F | F | F | F |
| dist[] | 0 | 4 | 3 | 7 | 12 | inf | 15 | inf |
| path[] | -1 | 0 | 0 | 1 | 1 | -1 | 2 | -1 |
第五步:继续第二步操作,找到节点v3
节点3相邻的节点有v5 v4
dist[4] = min(dist[3]+3,dist[4])=dist[3]+3=7+3 = 10
dist[5] = min(dist[3]+12,dist[5])=dist[3]+12=7+12 = 19
path[4] = path[5] = 3
更新完毕 标志节点已访问
visited[3] = true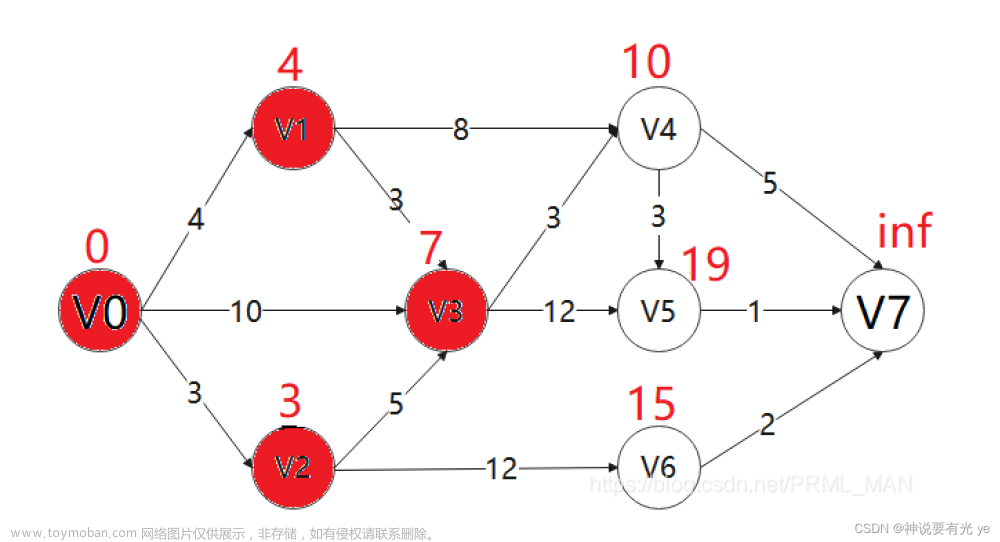
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|
| visited[] | T | T | T | T | F | F | F | F |
| dist[] | 0 | 4 | 3 | 7 | 10 | 19 | 15 | inf |
| path[] | -1 | 0 | 0 | 1 | 3 | 3 | 2 | -1 |
第六步:继续第二步操作,找到节点v4
节点3相邻的节点有v5 v7
dist[7] = min(dist[4]+5,dist[7])=dist[4]+5=10+5 = 15
dist[5] = min(dist[4]+3,dist[5])=dist[4]+3=10+3 = 13
path[7] = path[5] = 4
更新完毕 标志节点已访问
visited[4] = true

| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|
| visited[] | T | T | T | T | T | F | F | F |
| dist[] | 0 | 4 | 3 | 7 | 10 | 13 | 15 | 15 |
| path[] | -1 | 0 | 0 | 1 | 3 | 4 | 2 | 4 |
第七步:继续第二步操作,找到节点v5
节点5相邻的节点有v7
dist[7] = min(dist[5]+1,dist[7])=dist[5]+1=13+1 = 14
path[7] = 5
更新完毕 标志节点已访问
visited[5] = true

| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|
| visited[] | T | T | T | T | T | T | F | F |
| dist[] | 0 | 4 | 3 | 7 | 10 | 13 | 15 | 14 |
| path[] | -1 | 0 | 0 | 1 | 3 | 4 | 2 | 5 |
第七步:找到节点v7 结束
visited[7] = true

到达了目标节点了 路径长度为14
路径:v0->v1->v3->v4->v5->v7
代码实现
const graph = new Array(9).fill(0).map(item=>new Array(9).fill(-1))
const config = [
{
path:[0,1],
val:4
},
{
path:[0,3],
val:10
},
{
path:[0,2],
val:3
},
{
path:[2,6],
val:12
},
{
path:[2,3],
val:5
},
{
path:[1,3],
val:3
},
{
path:[1,4],
val:8
},
{
path:[3,4],
val:3
},
{
path:[3,5],
val:12
},
{
path:[4,5],
val:3
},
{
path:[4,7],
val:5
},
{
path:[5,7],
val:1
},
{
path:[6,7],
val:2
},
]
for(let i=0;i<config.length;i++){
const {path,val} = config[i]
graph[path[0]][path[1]] = val
}
const dijkstra = (graph,begin,end)=>{
// dist数组
const n = graph.length
const dist = new Array(n).fill(Number.MAX_SAFE_INTEGER)
const visited = new Array(n).fill(false)
const path = new Array(n).fill(-1)
// 初始化
dist[begin] = 0
// 开始查找
while(visited.includes(false)){
// 找最小值
let min = Number.MAX_SAFE_INTEGER
let minIndex = -1
for(let i=0;i<n;i++){
if(dist[i]<min&!visited[i]){
min = dist[i]
minIndex = i
}
}
if(minIndex===-1||minIndex===end) break
// 找相邻点
const arr = graph[minIndex]
for(let j=0;j<n;j++){
// 找到相邻点
if(arr[j]!==-1){
// 需要更新
if(j!=minIndex&&dist[j]>dist[minIndex]+arr[j]){
dist[j] = dist[minIndex]+arr[j]
path[j] = minIndex
}
}
}
// 标记访问
visited[minIndex] = true
}
// 输出路径
const patharr = [end]
while(patharr[0]!=begin){
patharr.unshift(path[patharr[0]])
}
console.log("路径",patharr)
return dist[end]
}
console.log(dijkstra(graph,0,7))
弗洛伊德算法 Floyd
Floyd算法是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法
算法核心思想:
对于一个图来说,从任意节点i到任意节点j的最短路径不外乎2种可能
第1种是直接从i到j
第2种是从i经过若干个节点k到j。
所以,我们假设distance(i,j)为节点u到节点v的最短路径的距离,对于每一个节点k,我们检查distance(i,k) + distance(k,j) < Dis(i,j)是否成立,如果成立,证明从i到k再到j的路径比i直接到j的路径短,我们便设置distance(i,j) = distance(i,k) + distance(k,j),这样一来,当我们遍历完所有节点k,distance (i,j)中记录的便是i到j的最短路径的距离。
状态转移方程:
distance[i][j] = min{distance[i][k] + distance[k][j],distance[i][j]}
例子:
第一步:初始化

dist[i][j]表示i到j的最短路径,inf表示i到达不了j
path[i][j]存储的是i到j的中转节点,-1表示没有中转节点
dist[][]
| 下标 | 1 | 2 | 3 | 4 | 5 |
| 1 | 0 | 3 | 10 | inf | inf |
| 2 | 3 | 0 | inf | 5 | inf |
| 3 | 10 | inf | 0 | 6 | 15 |
| 4 | inf | 5 | 6 | 0 | 4 |
| 5 | inf | inf | inf | 4 | 0 |
path[][]文章来源:https://www.toymoban.com/news/detail-745174.html
| 下标 | -1 | -1 | -1 | -1 | -1 |
| 1 | -1 | -1 | -1 | -1 | -1 |
| 2 | -1 | -1 | -1 | -1 | -1 |
| 3 | -1 | -1 | -1 | -1 | -1 |
| 4 | -1 | -1 | -1 | -1 | -1 |
| 5 | -1 | -1 | -1 | -1 | -1 |
第二步:以v1为中转站
v2通过v1到达v3
v3通过v1到达v2
dist[2][3] = min(dist[2][1]+dist[1][3],dist[2][3]) = dist[2][1]+dist[1][3] = 3+10 = 13
dist[3][2] = min(dist[3][1]+dist[1][2],dist[2][2]) = dist[3][1]+dist[1][2] = 10+3 = 13
path[2][3] = 1
path[3][2] = 1

dist[][]
| 下标 | 1 | 2 | 3 | 4 | 5 |
| 1 | 0 | 3 | 10 | inf | inf |
| 2 | 3 | 0 | 13 | 5 | inf |
| 3 | 10 | 13 | 0 | 6 | 15 |
| 4 | inf | 5 | 6 | 0 | 4 |
| 5 | inf | inf | inf | 4 | 0 |
path[][]
| 下标 | 1 | 2 | 3 | 4 | 5 |
| 1 | -1 | -1 | -1 | -1 | -1 |
| 2 | -1 | -1 | 1 | -1 | -1 |
| 3 | -1 | 1 | -1 | -1 | -1 |
| 4 | -1 | -1 | -1 | -1 | -1 |
| 5 | -1 | -1 | -1 | -1 | -1 |
第三步:以v2为中转站
跟v2有连接的点有v1 v3 v4
因此 得出下面的关系:
v1通过v2到达v4
v4通过v2到达v1
dist[1][4] = min(dist[1][2]+dist[2][4],dist[1][4]) = dist[1][2]+dist[2][4] = 3+5 = 8
dist[4][1] = min(dist[4][2]+dist[2][1],dist[4][1]) = dist[4][2]+dist[2][1] = 5+3 = 8
path[1][4] = 2
path[4][1] = 2
v1通过v2到达v3
v3通过v2到达v1
dist[1][3] = min(dist[1][2]+dist[2][3],dist[1][3]) = dist[1][3]
dist[3][1] = min(dist[3][2]+dist[2][1],dist[3][1]) = dist[3][1]
可以看到 并没有更新 还是以前的值 所以就不需要更新path,因为并没有借助v2中转站更新值
v3通过v2到达v4
v4通过v2到达v3
dist[3][4] = min(dist[3][2]+dist[2][4],dist[3][4]) = dist[3][4]
dist[4][3] = min(dist[4][2]+dist[2][3],dist[4][3]) = dist[4][3]
可以看到 并没有更新 还是以前的值 所以就不需要更新path,因为并没有借助v2中转站更新值

dist[][]
| 下标 | 1 | 2 | 3 | 4 | 5 |
| 1 | 0 | 3 | 10 | 8 | inf |
| 2 | 3 | 0 | 13 | 5 | inf |
| 3 | 10 | 13 | 0 | 6 | 15 |
| 4 | 8 | 5 | 6 | 0 | 4 |
| 5 | inf | inf | inf | 4 | 0 |
path[][]
| 下标 | 1 | 2 | 3 | 4 | 5 |
| 1 | -1 | -1 | -1 | 2 | -1 |
| 2 | -1 | -1 | 1 | -1 | -1 |
| 3 | -1 | 1 | -1 | -1 | -1 |
| 4 | 2 | -1 | -1 | -1 | -1 |
| 5 | -1 | -1 | -1 | -1 | -1 |
第四步:以v3为中转站
跟v3有连接的点有v1 v2 v4 v5,这里需要注意v3到v5是单向边
因此 得出下面的关系:
v1通过v3到达v2
v2通过v3到达v1
dist[1][2] = min(dist[1][3]+dist[3][2],dist[1][2]) = dist[1][2]
dist[2][1] = min(dist[2][3]+dist[3][1],dist[2][1]) = dist[2][1]
可以看到 并没有更新 还是以前的值 所以就不需要更新path,因为并没有借助v3中转站更新值
v1通过v3到达v4
v4通过v3到达v1
dist[1][4] = min(dist[1][3]+dist[3][4],dist[1][4]) = dist[1][4]
dist[4][1] = min(dist[4][3]+dist[3][1],dist[4][1]) = dist[4][1]
可以看到 并没有更新 还是以前的值 所以就不需要更新path,因为并没有借助v3中转站更新值
v1通过v3到达v5
因为v3->v5是单向边 所以v5到达不了v3,无法更新dist[5][1]
dist[1][5] = min(dist[1][3]+dist[3][5],dist[1][5]) =dist[1][3]+dist[3][5] = 10=15=25
path[1][5] = 3
v2通过v3到达v5
因为v3->v5是单向边 所以v5到达不了v3,无法更新dist[5][2]
dist[2][5] = min(dist[2][3]+dist[3][5],dist[2][5]) =dist[2][3]+dist[3][5] = 13=15=28
path[2][5] = 3
v2通过v3到达v4
v4通过v3到达v2
dist[2][4] = min(dist[2][3]+dist[3][4],dist[2][4]) = dist[2][4]
dist[4][2] = min(dist[4][3]+dist[3][2],dist[4][2]) = dist[4][2]
可以看到 并没有更新 还是以前的值 所以就不需要更新path,因为并没有借助v3中转站更新值
v4通过v3到达v5
因为v3->v5是单向边 所以v5到达不了v3,无法更新dist[5][4]
dist[4][5] = min(dist[4][3]+dist[3][5],dist[4][5]) =dist[4][5]
可以看到 并没有更新 还是以前的值 所以就不需要更新path,因为并没有借助v3中转站更新值

dist[][]
| 下标 | 1 | 2 | 3 | 4 | 5 |
| 1 | 0 | 3 | 10 | 8 | 25 |
| 2 | 3 | 0 | 13 | 5 | 28 |
| 3 | 10 | 13 | 0 | 6 | 15 |
| 4 | 8 | 5 | 6 | 0 | 4 |
| 5 | inf | inf | inf | 4 | 0 |
path[][]
| 下标 | 1 | 2 | 3 | 4 | 5 |
| 1 | -1 | -1 | -1 | 2 | 3 |
| 2 | -1 | -1 | 1 | -1 | 3 |
| 3 | -1 | 1 | -1 | -1 | -1 |
| 4 | 2 | -1 | -1 | -1 | -1 |
| 5 | -1 | -1 | -1 | -1 | -1 |
第五步:以v4为中转站
跟v4有连接的点有v2 v1 v3 v5
因此 得出下面的关系:
v1通过v4到达v2
v2通过v4到达v1
dist[1][2] = min(dist[1][4]+dist[4][2],dist[1][2]) = dist[1][2]
dist[2][1] = min(dist[2][4]+dist[4][1],dist[2][1]) = dist[2][1]
可以看到 并没有更新 还是以前的值 所以就不需要更新path,因为并没有借助v4中转站更新值
v1通过v4到达v3
v3通过v4到达v1
dist[1][3] = min(dist[1][4]+dist[4][3],dist[1][3]) = dist[1][3]
dist[3][1] = min(dist[3][4]+dist[4][1],dist[3][1]) = dist[3][1]
可以看到 并没有更新 还是以前的值 所以就不需要更新path,因为并没有借助v4中转站更新值
v1通过v4到达v5
v5通过v4到达v1
dist[1][5] = min(dist[1][4]+dist[4][5],dist[1][5]) = dist[1][4]+dist[4][5] = 8+4=12
dist[5][1] = min(dist[5][4]+dist[4][1],dist[5][1]) = 4+8=12
path[1][5] =path[5][1] = 4
v2通过v4到达v3
v3通过v4到达v2
dist[2][3] = min(dist[2][4]+dist[4][3],dist[2][3]) = dist[2][4]+dist[4][3] = 5+6=11
dist[3][2] = min(dist[3][4]+dist[4][2],dist[3][2]) = dist[3][4]+dist[4][2] = 6+5=11
path[2][3] =path[3][2] = 4
v2通过v4到达v5
v5通过v4到达v2
dist[2][5] = min(dist[2][4]+dist[4][5],dist[2][5]) = dist[2][4]+dist[4][5] = 5+4=9
dist[5][2] = min(dist[5][4]+dist[4][2],dist[5][2]) = dist[5][4]+dist[4][2] = 4+5=9
path[2][5] =path[5][2] = 4
v3通过v4到达v5
v5通过v4到达v3
dist[3][5] = min(dist[3][4]+dist[4][5],dist[3][5]) =dist[3][4]+dist[4][5] = 4+6=10
dist[5][3] = min(dist[5][4]+dist[4][3],dist[5][3]) = dist[5][4]+dist[4][3] = 6+4=10
path[3][5] = path[5][3] = 10

dist[][]
| 下标 | 1 | 2 | 3 | 4 | 5 |
| 1 | 0 | 3 | 10 | 8 | 12 |
| 2 | 3 | 0 | 11 | 5 | 9 |
| 3 | 10 | 11 | 0 | 6 | 10 |
| 4 | 8 | 5 | 6 | 0 | 4 |
| 5 | 12 | 9 | 10 | 4 | 0 |
path[][]
| 下标 | 1 | 2 | 3 | 4 | 5 |
| 1 | -1 | -1 | -1 | 2 | 4 |
| 2 | -1 | -1 | 4 | -1 | 4 |
| 3 | -1 | 4 | -1 | -1 | 4 |
| 4 | 2 | -1 | -1 | -1 | -1 |
| 5 | 4 | 4 | 4 | -1 | -1 |
第六步:以v5为中转站
跟v5有连接的点有v2 v1 v3 v4
因此 得出下面的关系:
v1通过v5到达v2
v2通过v5到达v1
dist[1][2] = min(dist[1][5]+dist[5][2],dist[1][2]) = dist[1][2]
dist[2][1] = min(dist[2][5]+dist[5][1],dist[2][1]) = dist[2][1]
可以看到 并没有更新 还是以前的值 所以就不需要更新path,因为并没有借助v4中转站更新值
v1通过v5到达v3
v3通过v5到达v1
dist[1][3] = min(dist[1][5]+dist[5][3],dist[1][3]) = dist[1][3]
dist[3][1] = min(dist[3][5]+dist[5][1],dist[3][1]) = dist[3][1]
可以看到 并没有更新 还是以前的值 所以就不需要更新path,因为并没有借助v4中转站更新值
v1通过v5到达v4
v4通过v5到达v1
dist[1][4] = min(dist[1][5]+dist[5][4],dist[1][4]) = dist[1][4]
dist[4][1] = min(dist[4][5]+dist[5][1],dist[4][1]) = dist[4][1]
可以看到 并没有更新 还是以前的值 所以就不需要更新path,因为并没有借助v4中转站更新值
v2通过v5到达v3
v3通过v5到达v2
dist[2][3] = min(dist[2][5]+dist[5][3],dist[2][3]) = dist[2][3]
dist[3][2] = min(dist[3][5]+dist[5][2],dist[3][2]) = dist[3][2]
可以看到 并没有更新 还是以前的值 所以就不需要更新path,因为并没有借助v4中转站更新值
v2通过v5到达v4
v4通过v5到达v2
dist[2][4] = min(dist[2][5]+dist[5][4],dist[2][4]) = dist[2][4]
dist[4][2] = min(dist[4][5]+dist[5][2],dist[4][2]) = dist[4][2]
可以看到 并没有更新 还是以前的值 所以就不需要更新path,因为并没有借助v4中转站更新值
v3通过v5到达v4
v4通过v5到达v3
dist[3][4] = min(dist[3][5]+dist[5][4],dist[3][4]) = dist[3][4]
dist[4][3] = min(dist[4][5]+dist[5][3],dist[4][3]) = dist[4][3]
可以看到 并没有更新 还是以前的值 所以就不需要更新path,因为并没有借助v4中转站更新值

dist[][]
| 下标 | 1 | 2 | 3 | 4 | 5 |
| 1 | 0 | 3 | 10 | 8 | 12 |
| 2 | 3 | 0 | 11 | 5 | 9 |
| 3 | 10 | 11 | 0 | 6 | 10 |
| 4 | 8 | 5 | 6 | 0 | 4 |
| 5 | 12 | 9 | 10 | 4 | 0 |
path[][]
| 下标 | 1 | 2 | 3 | 4 | 5 |
| 1 | -1 | -1 | -1 | 2 | 4 |
| 2 | -1 | -1 | 4 | -1 | 4 |
| 3 | -1 | 4 | -1 | -1 | 4 |
| 4 | 2 | -1 | -1 | -1 | -1 |
| 5 | 4 | 4 | 4 | -1 | -1 |
第七步:遍历完毕,输出结果文章来源地址https://www.toymoban.com/news/detail-745174.html
代码实现
const graph = new Array(6).fill(0).map(item=>new Array(6).fill(-1))
const config = [
{
path:[1,2],
val:3
},
{
path:[1,3],
val:10
},
{
path:[2,1],
val:3
},
{
path:[2,4],
val:5
},
{
path:[3,1],
val:10
},
{
path:[3,4],
val:6
},
{
path:[3,5],
val:15
},
{
path:[4,2],
val:5
},
{
path:[4,3],
val:6
},
{
path:[4,5],
val:4
},
{
path:[5,4],
val:4
},
]
for(let i=0;i<config.length;i++){
const {path,val} = config[i]
graph[path[0]][path[1]] = val
}
const floyd = (graph)=>{
const n = graph.length
const dist = new Array(n).fill(0).map(item=>new Array(n).fill(Number.MAX_SAFE_INTEGER))
const path = new Array(n).fill(0).map(item=>new Array(n).fill(-1))
//初始化
for(let i=1;i<n;i++){
for(let j=1;j<n;j++){
if(graph[i][j]!==-1){
dist[i][j] = graph[i][j]
}
if(i===j){
dist[i][j] = 0
}
}
}
// 遍历中转节点
for(let k=1;k<n;k++){
// 起始点
for(let i=1;i<n;i++){
// 结束点
for(let j=1;j<n;j++){
// 符合更新条件
if(dist[i][k]+dist[k][j]<dist[i][j]){
dist[i][j] = dist[i][k]+dist[k][j]
path[i][j] = k
}
}
}
}
// 输出路径
for(let i=1;i<n;i++){
for(let j=1;j<n;j++){
if(dist[i][j]===Number.MAX_SAFE_INTEGER){
console.log(`${i}到${j}没有连通路径`)
}
if(i!==j&&dist[i][j]!==Number.MAX_SAFE_INTEGER){
console.log(`${i}到${j}最短路径长度为:${dist[i][j]}`)
let k = path[i][j]
const pathArr = []
// 输出路径
while(k != j && k!=-1){
pathArr.unshift(k)
k= path[i][k];
}
const str = pathArr.length?`${i}->${pathArr.join('->')}->${j}`:`${i}->${j}`
console.log("路径:",str)
}
}
}
}
floyd(graph)
到了这里,关于详解图的最短路径算法(BFS、Dijkstra、Floyd)(附上图解步骤)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!













