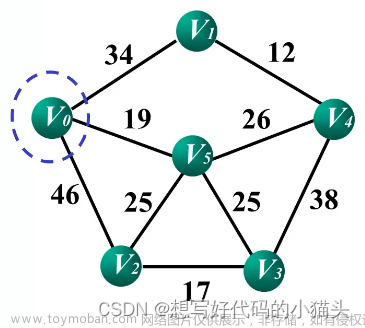
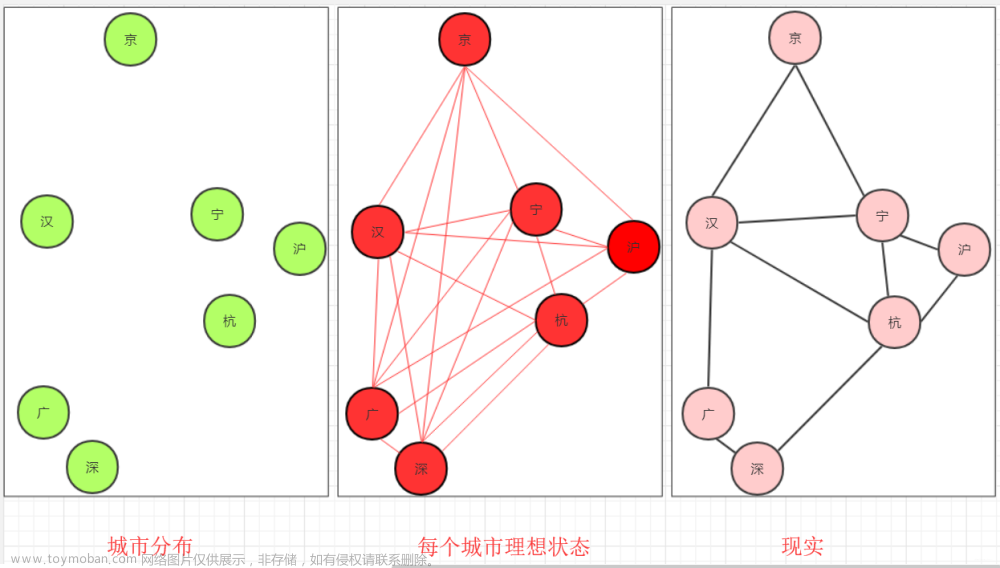
想求最小生成树,我们首先得弄懂以下几个概念

连通图:图中任意两个顶点都是连通的
极小连通子图:既要保持图连通又要使得边数最少的子图
生成树: 包含图中全部顶点的一个极小连通子图
连通图用通俗的话来讲就是,某一个顶点,可以直接或者间接(通过其他顶点)到达图上的所有顶点
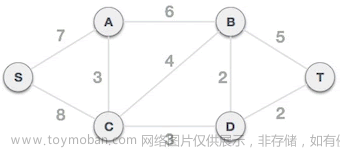
而在相邻2个顶点的每一条边都可以被赋予一定的权值,求最小生成树就是在原来被赋予权值连通图上,先暂时去掉所有边,通过某种算法,构造出 边数最少,所有边权值和最小的 生成树
这样的树被称为, 最小生成树
我们这样用两种算法去解答,分别是Prim(普里姆)算法和Kruskal(克鲁斯卡尔)算法
Prim(普里姆)

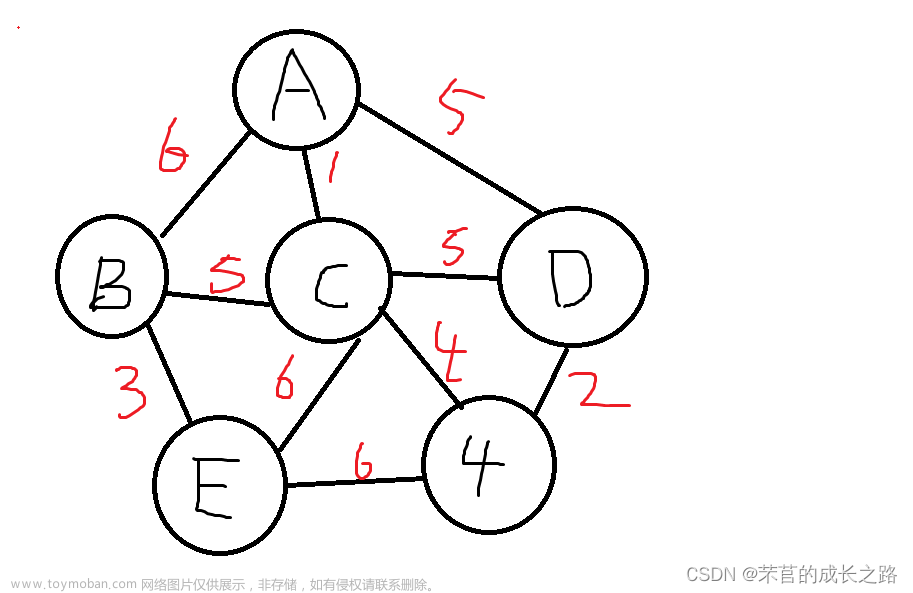
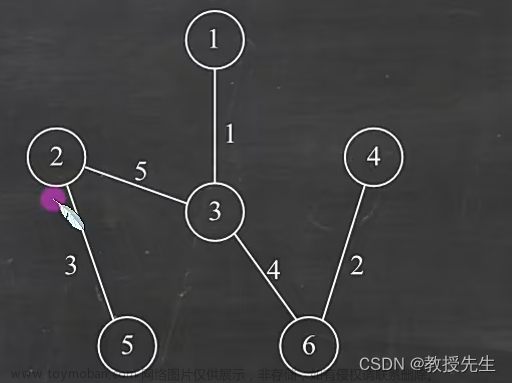
(1)首先,任取一个点,比如说取节点1,将1加入 顶点集合 {1}
(2)从顶点集合中选择节点1,周围有3个边可选(6,1,5),选择其中最小的1,然后连接上(1-3),然后将3加入顶点集合{1、3},

文章来源地址https://www.toymoban.com/news/detail-745328.html
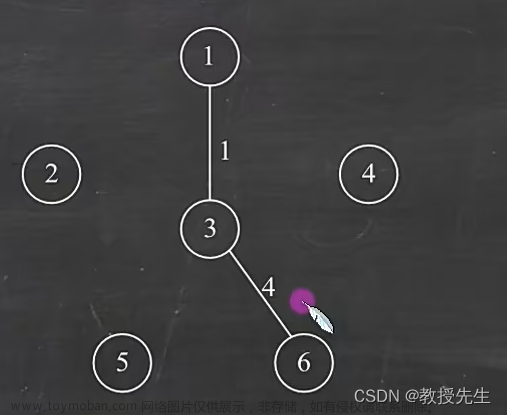
(3)从顶点集合中选择,不能是连接过的边,周围有6个边可选(6、5、5、5、6、4),选择其中最小的4,然后连接上(3-6),然后将6加入顶点集合{1、3、6},
文章来源:https://www.toymoban.com/news/detail-745328.html
(4)从顶点集合中选择,不能是连接过的边,周围有7个边可选(6、5、5、5、6、6、2),选择其中最小的2,然后连接上(6-4),然后将4加入顶点集合{1、3、6、4},
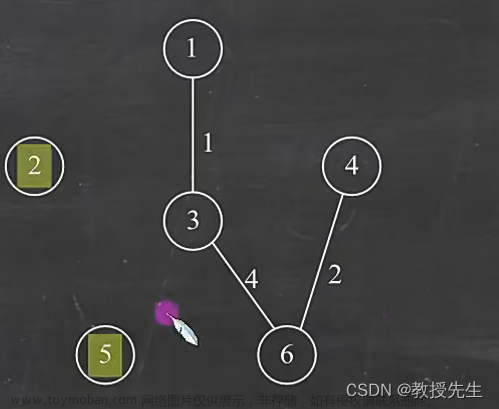
(5)从顶点集合中选择,不能是连接过的边,连接的边不能形成回路,周围有4个边可选(6、5、6、6),(两个边5因为不能形成闭合回路删除了,加上连接过的2)选择其中最小的5,然后连接上(3-2),然后将2加入顶点集合{1、3、6、4、2},
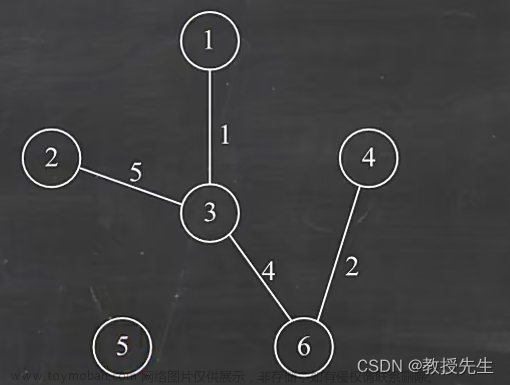
(5)从顶点集合中选择,不能是连接过的边,连接的边不能形成回路,周围有3个边可选(6、3、6),(一个边6因为不能形成闭合回路删除了,加上连接过的5,增加了一个3)选择其中最小的3,然后连接上(2-5),然后将5加入顶点集合{1、3、6、4、2、5},
至此,所有顶点都并入顶点集合完毕,算法运行结束。所以如图呈现的便是最小生成树。
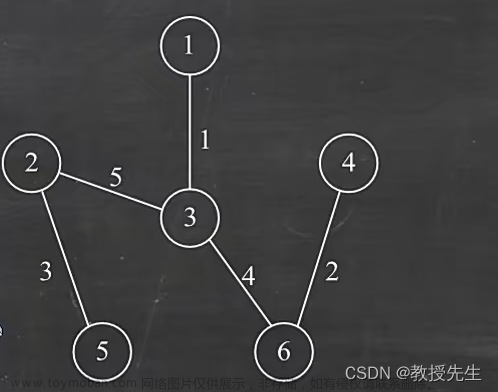
以上是Prim算法
现在我要介绍的是Kruskal(克鲁斯卡尔)算法

我自认为这个算法比较简单,容易理解
首先去掉所有边,然后把所有权值的边都列出来,按照从小到大的顺序依次放回原图中,如果放回的边构成回路,则选取下一个(稍大一点的边)再放回图中,直至将所有顶点都连接起来,(有个小细节:每连接好一条线,就可以将连接线的两个顶点加入顶点集合当中,当判断到顶点数==边数+1的时候,最小生成树完成,程序结束)(所有最小生成树都符合顶点数==边数+1这个规律)
1、具体举例将所有边的权值按照从小到大排序(12 3 4 5 5 5 6 6 6),共10个,

(12 3 4 5 5 5 6 6 6)
2、选取最小的1,并删除,将1对应的边放回原图中,1、3顶点并入顶点集合{1、3},这时有1条边
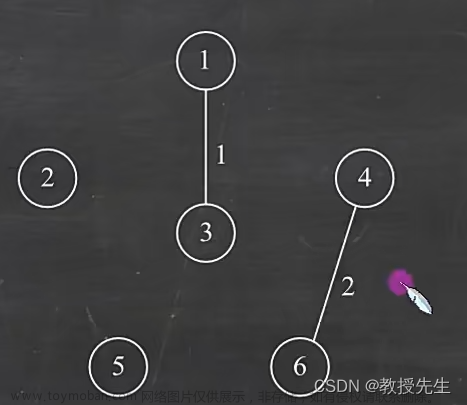
(2 3 4 5 5 5 6 6 6)
3、选取最小的2,并删除,将2对应的边放回原图中,4、6顶点并入顶点集合{1、3、4、6},这时有2条边
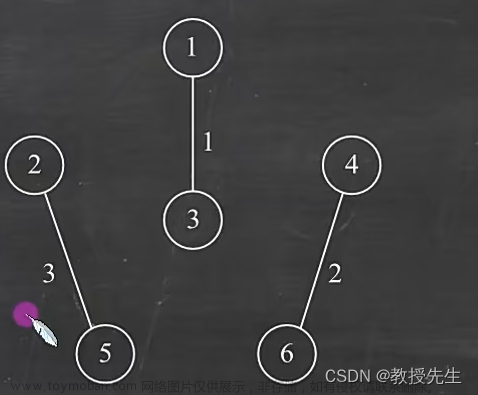
( 3 4 5 5 5 6 6 6)
4、选取最小的3,并删除,将3对应的边放回原图中,2、5顶点并入顶点集合{1、3、4、6、2、5},这时有3条边

( 4 5 5 5 6 6 6)
5、选取最小的4,并删除,将4对应的边放回原图中,3、6顶点并入顶点集合{1、3、4、6、2、5},原来有了,就不用增加,这时有4条边
( 5 5 5 6 6 6)
6、选取最小的5,并删除,将5对应的边放回原图中,2、3顶点并入顶点集合{1、3、4、6、2、5},原来有了,就不用增加.这时有5条边,当判断到顶点数==边数+1的时候,(6个顶点=5条边)最小生成树完成
到了这里,关于求最小生成树Prim(普里姆)和Kruskal(克鲁斯卡尔)算法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!