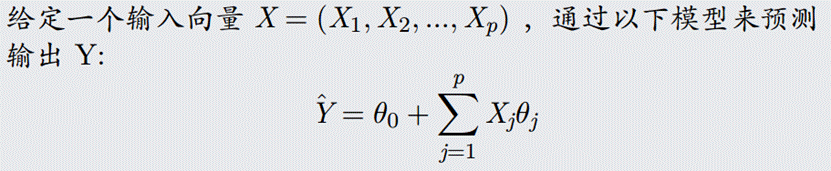实验内容
假设某披萨店的披萨价格和披萨直径之间有下列数据关系:
| 训练样本 | 直径(英寸) | 价格(美元) |
|---|---|---|
| 1 | 6 | 7 |
| 2 | 8 | 9 |
| 3 | 10 | 13 |
| 4 | 14 | 17.5 |
| 5 | 18 | 18 |
根据上面的训练数据,预测12英寸的披萨的可能售价。
1、直径为自变量X,价格为因变量y,画出二者的散点图,并给出结论。
2、根据现有的训练数据求线性回归模型,并画出拟合直线,给出拟合直线方程。
3、预测12英寸披萨的价格。
4、评价模型的准确率,分析模型预测结果
注:
测试数据:
| 训练样本 | 直径(英寸) | 价格(美元) |
|---|---|---|
| 1 | 8 | 8.5 |
| 2 | 9 | 11 |
| 3 | 11 | 12 |
| 4 | 12 | 15 |
| 5 | 16 | 18 |
实验内容
一、首先进行绘制散点图,绘制散点图我们使用matplotlib.pyplot库,直径、价格分别为自变量x,y,并且设置所画散点图的属性。
代码:
import matplotlib.pyplot as plt
data_x = [[6], [8], [10], [14], [18]]
data_y = [[7], [9], [13], [17.5], [18]]
plt.title("Pizza Price vs Diameter") # 设置标题名称
plt.xlim(0, 25) # 设置x轴坐标范围
plt.ylim(0, 25) # 设置y轴坐标范围
plt.xlabel('Diameter') # 设置x轴标题
plt.ylabel('Price') # 设置y轴标题
plt.plot(data_x, data_y, 'k.') #绘制散点图
plt.show()
运行结果:
注:
plt.plot(data_x, data_y, 'k.')
中'k.'为图形符号以及颜色风格的设置,现给出常用部分速查表:
| character | description | character | description |
|---|---|---|---|
| ‘.’ | 点标记 | ‘k’ | 黑色 |
| ‘-’ | 实线 | ‘g’ | 绿色 |
| ‘–’ | 虚线 | ‘r’ | 红色 |
| ‘-.’ | 点划线 | ‘b’ | 蓝色 |
| ‘:’ | 实点线 | ‘y’ | 黄色 |
二、使用sklearn.linear_model.LinearRegression对象进行拟合,首先创建一个线性回归对象,使用fit方法进行训练模型,再使用intercept_``lin_reg.coef_获得所得拟合方程的截距与斜率。为了方便绘制拟合方程图像,创建一个二位列表(data_x2)方便将方程直线绘制范围为增加到[0,25],再使用predict函数进行预测出所对应的y值,最后使用plot函数绘制拟合方程。
代码:
data_x2 = [[0], [10], [15], [25]]
model = linear_model.LinearRegression()
model.fit(data_x, data_y)
intercept = str(model.intercept_[0])[:4]
coef = str(model.coef_[0][0])[:4]
print("截距为:" + intercept)
print("斜率为:" + coef)
print("拟合直线方程为:" + "y=" + coef + "x+" + intercept)
data_y2 = model.predict(data_x2)
plt.plot(data_x2, data_y2, '-')
plt.show()
运行结果:


看完代码的小伙伴们可能会有疑问为什么会出现这样的代码
intercept = str(model.intercept_[0])[:4]
coef = str(model.coef_[0][0])[:4]
其实不难理解,我们先输出一下'model.intercept_' 'model.coef_'的输出结果:
是的,你没看错,'model.intercept_'输出的数据是一个列表,'model.coef_'更是一个二位列表,而题干要求我们输出拟合方程,如果截距和斜率居然用列表的形式表示出来,那岂不是成了四不像!所以我先将他们转化成字符串,最后保留小数点后两位数字。
三、在第二步我们已经通过model对象训练出模型,预测12英寸披萨的价格那就是再简单不过的事情了,我们只需要使用predict方法直接预测!
代码:
piece = str(model.predict([[12]])[0][0])[:5]
print("预测12英寸披萨的价格为:" + piece)
运行结果:

别再问我'str(model.predict([[12]])[0][0])[:5]'这是什么意思,往上翻!!!!
四、第四步就是考察你之前是否明白之前的所讲内容,话不多说,首先传入测试数据,画出散点图,使用之前的训练模型进行数据预测,最后使用model.score方法对模型准确率进行计算。
总代码:
import matplotlib.pyplot as plt
from sklearn import linear_model
def run_plt():
plt.rcParams['font.sans-serif'] = ['SimHei'] # 标题中文不报错
plt.title("Pizza Price vs Diameter")
plt.xlim(0, 25)
plt.ylim(0, 25)
plt.xlabel('Diameter')
plt.ylabel('Price')
return plt
if __name__ == "__main__":
# 题目一
plt = run_plt()
data_x = [[6], [8], [10], [14], [18]]
data_y = [[7], [9], [13], [17.5], [18]]
plt.plot(data_x, data_y, 'k.')
plt.show()
# 题目二
plt = run_plt()
plt.plot(data_x, data_y, 'k.')
data_x2 = [[0], [10], [15], [25]]
model = linear_model.LinearRegression()
model.fit(data_x, data_y)
print("截距为:" + str(model.intercept_[0])[:4])
print("斜率为:" + str(model.coef_[0][0])[:4])
data_y2 = model.predict(data_x2)
plt.plot(data_x2, data_y2, '-')
plt.show()
# 题目三
piece = str(model.predict([[12]])[0][0])[:5]
print("预测12英寸披萨的价格为:" + piece)
# 题目四
data_x_test = [[8], [9], [11], [12], [16]]
data_y_test = [[8.5], [11], [12], [15], [18]]
data_x2_test = [[6], [11], [14], [18]]
plt = run_plt()
plt.plot(data_x, data_y, 'k.')
plt.plot(data_x_test, data_y_test, 'r.')
data_y2_test = model.predict(data_x2_test)
plt.plot(data_x2_test, data_y2_test, '-')
plt.show()
# 计算模型准确率
print(model.score(data_x_test, data_y_test))
结果图:


 文章来源:https://www.toymoban.com/news/detail-745754.html
文章来源:https://www.toymoban.com/news/detail-745754.html
好啦,到这里这个实验就完成了,这是我第一次写博客,写的不好的地方请大家多多指教,对了,未来cust的学弟学妹们,你们的学长呕心沥血地写这个博客不是为了让你们“借鉴”的哦,学长的初衷是为了你们少走弯路哦!文章来源地址https://www.toymoban.com/news/detail-745754.html
到了这里,关于机器学习实验——单变量线性回归(披萨价格预测问题)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!