模拟赛好题分享

@

山茶花

性质推导题： 如果没有+1操作， 那么最后的答案一定为恒定的ans

考虑+1操作对什么时候会产生影响

不难发现，如果后缀为k个1, 则+1操作等效于 \(ans ^ (1 << (k + 1) )\)

那么问题就转化为了由这n任意顺序异或，是否可以异或出后缀为k个1的数

如果第0位的1都没有拼凑成功，那么后缀1再长也没有意义，所以如果要想异或出k个1，必须要保证前\(k - 1\)个1异或出来且不能因为第k位1的异或影响

思考线性基异或最大值时，保证了优先异或出高位1且高位1不会被低位1影响

所以可以构造低位线性基进行判断 复杂度\(n * log_{2}n\)

100pts

#include<bits/stdc++.h>
using namespace std;
#define LL long long 
const int MAX = 2e6 + 70;
int n;
LL a[MAX], b[MAX], SUM = 0, ans = 0;
void add(LL X) {
	for(int i = 0; i <= 61; i++) if(X >> i & 1) {
		if(b[i]) X ^= b[i];	
		else {
			b[i] = X;
//			printf("b[%d] %lld\n", i, b[i]);
			return ; 
		}
	}
}
bool check(int X) {
	LL NOW = 0;
	for(int i = 0; i <= X; i++) {
//		printf("X %d NOW %lld\n", X, NOW);
		if((NOW >> i & 1) != (i != X)) {
			if(b[i]) NOW ^= b[i];
			else return 0;	
		}
	}
	return 1;
}
int main() {
//	freopen("shuju.in","r",stdin);
//	freopen("mine.out","w",stdout); 
	scanf("%d", &n);
	for(int i = 1; i <= n; i++) {
		scanf("%lld", &a[i]);
		SUM ^= a[i];
		add(a[i]);	
	}
//	cout<<SUM<<endl;
	for(int i = 0; i <= 61; i++) { // 使末尾有i个1
		if(check(i)) {
			ans = max(ans, SUM ^ (1ll << (i + 1)) - 1);
//			printf("i %d %lld\n",i, ans);	
		} 
	}
	cout<<ans<<endl;
	return 0;
}

T1区间逆序对

60pts

1e5莫队即可，主要复习一下回滚莫队

#include<bits/stdc++.h>
using namespace std;
#define LL long long 
const int MAX = 1e6 + 70;
int n, m, a[MAX], bl[MAX], blen;
int t1[52], t2[52], k[52];
LL ANS[MAX];
struct made {
	int l, r, id;
}ask[MAX];
bool mycmp(made X, made Y) { return (bl[X.l] < bl[Y.l]) || (bl[X.l] == bl[Y.l] && X.r < Y.r); }
int lowbit(int x) { return (x & (-x)); }
void add1(int x) { for(int i = x; i; i -= lowbit(i)) t1[i] += 1; }
LL Find1(int x)  { LL res = 0; for(int i = x; i <= 50; i += lowbit(i)) res += t1[i]; return res;}
void add2(int x) { for(int i = x; i; i -= lowbit(i)) t2[i] += 1; }
LL Find2(int x) { LL res = 0; for(int i = x; i <= 50; i += lowbit(i)) res += t2[i]; return res;}
int main() {
	scanf("%d%d", &n, &m);
	blen = pow(n, 2.0 / 3.0);
//	printf("blen %d\n", blen);
	for(int i = 1; i <= n; i++) bl[i] = (i / blen) + 1;	
	for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
	for(int i = 1; i <= m; i++) {
		scanf("%d%d",&ask[i].l, &ask[i].r);
		ask[i].id = i;
	}
	sort(ask + 1, ask + 1 + m, mycmp);
	int LST = 0, L = 0, R = 0;
	LL ans = 0;
	for(int i = 1; i <= m; i++) {
		if(bl[ask[i].l] == bl[ask[i].r]) { //同一块中，暴力求解 
			memset(t1, 0, sizeof(t1)); LL res = 0;
			for(int j = ask[i].l; j <= ask[i].r; j++) {
				res += Find1(a[j] + 1);
				add1(a[j]);
			}
			ANS[ask[i].id] = res;
		} else {
//			printf("ask[%d].id %d l %d r %d\n", i, ask[i].id, ask[i].l, ask[i].r); 
			if(bl[ask[i].l] != LST) { //不在一个块中 
				memset(t2, 0, sizeof(t2));
				L = (blen * bl[ask[i].l]);
				R = L - 1;
				ans = 0;			
				LST = bl[ask[i].l];
			}
//			printf("L %d R %d\n", L, R);
			while(R < ask[i].r) {
				ans += Find2(a[++R] + 1);
				add2(a[R]);
			}
			LL res = ans; //储存 
			for(int j = 1; j <= 50; j++) k[j] = t2[j];
			while(L > ask[i].l) {
				L--;
				ans += (R - L - Find2(a[L]));
				add2(a[L]);
			}
			ANS[ask[i].id] = ans;
			ans = res;
			L = (blen * bl[ask[i].l]);
			for(int j = 1; j <= 50; j++) t2[j] = k[j]; //撤销 
		}
		
	}
	for(int i = 1; i <= m; i++) printf("%lld\n", ANS[i]);
	return 0;
}

100pts 区间操作固定套路，转化为前缀操作

观察数据范围， a的数值都小于等于50， 而每次查询都是一个区间，面对区间问题，最常用的套路就是预处理出前缀数组，O(常数)查询
思考前缀逆序对F性质，对于区间L,R而言， 前缀F[R] 包含了 \(L < l < r < R,l < r < L, l < L < r < R\) 三种逆序对

对于前两种逆序对，F[R] - F[L] 即可， 主要需要撤销l不在[L,R]中， r在[L, R]中的逆序对， 这里就需要利用\(a <= 50\), 看[L, R]中每种1-50出现了多少次即可

#include<bits/stdc++.h>
using namespace std;
#define LL long long 
const LL MAX = 1e6 + 70;
int tree_g[MAX];
int tree_n[MAX];
int a[MAX];
LL n, m;
int sum[MAX][52];
LL NINI[MAX];
int num[MAX][52];
int lowbit(int x) {
	return (x & (-x));
}
int Find_g(int x) {
	int res = 0;
	for(int i = x; i <= 50; i += lowbit(i)) res += tree_g[i];
	return res;
}
void ADD_g(int x) {
	for(int i = x; i; i -= lowbit(i)) tree_g[i] += 1;
}
int Find_n(int x) {
	int res = 0;
	for(int i = x; i <= 50; i += lowbit(i)) res += tree_n[i];
	return res;
}
void ADD_n(int x) {
	for(int i = x; i; i -= lowbit(i)) tree_n[i] += 1;
}
signed main() {
//	freopen("ex_data3.in","r",stdin);
//	freopen("mine.out","w",stdout);
	scanf("%lld%lld", &n, &m);
	for(int i = 1; i <= n; i++) scanf("%d", &a[i]);	
	for(int i = 1; i <= n; i++) {
		for(int j = 1; j <= 50; j++) {
			sum[i][j] = sum[i - 1][j];
		}
		sum[i][a[i]] += 1;
	}
	for(int i = 1; i <= n; i++) { //处理前缀中比j大的个数 
		ADD_g(a[i]);
		for(int j = 1; j <= 50; j++) {
			num[i][j] = Find_g(j + 1);
		}
	}
	for(int i = 1; i <= n; i++) {
		NINI[i] = NINI[i - 1];
		LL res = Find_n(a[i] + 1);
		NINI[i] += res;
		ADD_n(a[i]);
	}
//	printf("%lld\n", num[2][2]);
	for(int i = 1; i <= m; i++) {
		int l, r; scanf("%d%d", &l, &r);
		LL ans = NINI[r] - NINI[l - 1];
		for(int j = 1; j <= 50; j++) {
			ans = ans - ((LL)num[l - 1][j] * (LL)(sum[r][j] - sum[l - 1][j]));
		}
		printf("%lld\n", ans);
	}
	return 0;
}

dream

20pts 神奇分块

对于\(n * m <= 5e7\)的数据考虑分块做法，发现如果没有回归操作，那么仅需要树状数组即可维护，但是我们发现对于序列(l, r)而言， 尽管它们的标记点不同，但是通过一次回归将所有标记清空后对于它们整体的操作所带来的偏移量一样！那么就可以分块解决了

没调过的代码

杭州:转化题意，正难则反

数据范围 \(n,m <= 200000\),首先很明显的事情，在一颗树中距离\(x\)最远的点一定是该直径的其中一个端点

那么题目要求我们求得就是在原树中任一子树的直径端点分别是什么，但是我们无法维护任一形态的子树

正难则反(或者对于这种有删边操作的题)， 我们看成反向加边

那么现在我们要求的就是合并两个联通块后直径端点是什么

假设两个联通块分别为S1,S2, 直径端点分别\(S1.L, S1.R S2.L, S2.R\), 连通块交点为X, 在两个连通块中距离X的最远的端点都在直径端点上

X将两个连通块联通，若直径没变，则应该为S1,S2中直径更大值，若发生改变，则一定经过X，所以发生更改的最远直径的端点一定为\(S1.L,S1.R,S2.L,S2.R\)

现在我们可以维护出连通块的最长直径和直径端点，因为这两个联通块合并后再在原树(假定1为根)中形态不变

所以用(DEP[X] + DEP[Y] - DEP[LCA(X,Y)])维护即可

//查询距离x最远的点，一定为树上直径端点之一， 删边树的直径不好维护
//考虑转化为加边维护联通块中的树的直径， 那么需要对于每次加边操作就重新跑一遍lca吗？
//显然不需要， 如果我们处理出整颗树，那么我们只需要确定那两个点是树的直径, 在原树中确定即可 
//不关心树的形态，只关心直径的端点 
#include<bits/stdc++.h>
using namespace std;
#define LL long long 
const int MAX = 2e5 + 70;
int n, m, cut[MAX], dep[MAX], tot, head[MAX];
int father[MAX], ANS[MAX], fa[MAX][22];
struct NODE {int x, y, dis;} p[MAX]; //分别表示这个点所处的联通块的直径端点和直径长度 
struct made { int l, t, id;}edge[MAX * 2], E[MAX];
struct ASK{ int op, x; }ask[MAX];
void add(int u, int v, int id) {
	edge[++tot].l = head[u];
	edge[tot].t = v; 
	edge[tot].id = id;
	head[u] = tot;
} 
void dfs(int x, int FA, int DEP) { //预处理整颗树的fa 
	fa[x][0] = FA; dep[x] = DEP;
	for(int i = 1; i <= 20; i++) fa[x][i] = fa[fa[x][i - 1]][i - 1];
	for(int i = head[x]; i; i = edge[i].l) {
		int t = edge[i].t;
		if(t == FA) continue;
		dfs(t, x, DEP + 1); 
	} 
}
int Find(int x) { return father[x] == x ? x : Find(father[x]); }
LL LCA(int x, int y) {
	if(dep[x] < dep[y]) swap(x, y);
	for(int i = 20; i >= 0; i--) if(dep[fa[x][i]] >= dep[y]) x = fa[x][i]; //往上跳
	if(x == y) return y;
	for(int i = 20; i >= 0; i--) if(fa[x][i] != fa[y][i]) x = fa[x][i], y = fa[y][i];
	return fa[y][0];
}
int check(int x, int y) { return (dep[x] + dep[y]) - 2 * dep[LCA(x, y)]; }
NODE mrg(NODE X, NODE Y) {
	NODE NOW = (X.dis > Y.dis) ? X : Y;
//	printf("NOW %d X.x %d X.y %d Y.x %d Y.y %d \n",NOW.dis, X.x, X.y, Y.x, Y.y);
	if(check(X.x, Y.x) > NOW.dis) {	
		NOW = {(NODE){X.x, Y.x, check(X.x, Y.x)}};
//		printf("FIRST NOW.x %d NOW.y %d NOW.dis %d\n", NOW.x, NOW.y, NOW.dis);
	} 
	if(check(X.x, Y.y) > NOW.dis) {
		NOW = {(NODE){X.x, Y.y, check(X.x, Y.y)}};
//		printf("SECOND NOW.x %d NOW.y %d NOW.dis %d\n", NOW.x, NOW.y, NOW.dis);
	} 
	if(check(X.y, Y.x) > NOW.dis) {
		NOW = {(NODE){X.y, Y.x, check(X.y, Y.x)}};		
//		printf("THIRD NOW.x %d NOW.y %d NOW.dis %d\n", NOW.x, NOW.y, NOW.dis);
	} 
	if(check(X.y, Y.y) > NOW.dis) {
//		printf("FORTH NOW.x %d NOW.y %d NOW.dis %d\n", NOW.x, NOW.y, NOW.dis);		
		NOW = {(NODE){X.y, Y.y, check(X.y, Y.y)}};
	} 
	return NOW;
}
void merge(int x, int y) {
	int fx = Find(x), fy = Find(y);
	father[fx] = fy;
//	printf("fx %d fy %d\n", fx, fy);
	p[fy] = mrg(p[fx], p[fy]); //直径 
}
void work() {
	dfs(1, 0, 0);
	for(int i = 1; i <= n; i++) father[i] = i, p[i] = {i, i, 0};
	for(int i = 1; i < n; i++) {
		if(cut[i] == 0) {
//			printf("E[%d] u %d v %d\n", i, E[i].l, E[i].t);
			merge(E[i].l, E[i].t); //合并两个联通块 
		}
	}
	for(int i = 1; i <= n; i++) {
		int fx = Find(i);
//		printf("i %d fa %d l %d r %d\n", i, fx, p[fx].x, p[fx].y);
	}
	for(int i = m; i >= 1; i--) {
		if(ask[i].op == 1) merge(E[ask[i].x].l, E[ask[i].x].t);
		else {
			int fx = Find(ask[i].x);	
			ANS[i] = max(check(ask[i].x, p[fx].x), check(ask[i].x, p[fx].y));
		} 
	}
}
int main() {
	scanf("%d%d", &n, &m);
	for(int i = 1; i < n; i++) {
		int u, v; scanf("%d%d", &u, &v);
		add(u, v, i); add(v, u, i);
		E[i] = {(made){u, v, i}};
	} 
	for(int i = 1; i <= m; i++) {
		scanf("%d%d", &ask[i].op, &ask[i].x);
		if(ask[i].op == 1) cut[ask[i].x] = 1;
	}
	memset(ANS, -1, sizeof(ANS));
	work(); //
	for(int i = 1; i <= m; i++) {
		if(ANS[i] != -1) printf("%d\n", ANS[i]);
	}
	return 0;
}

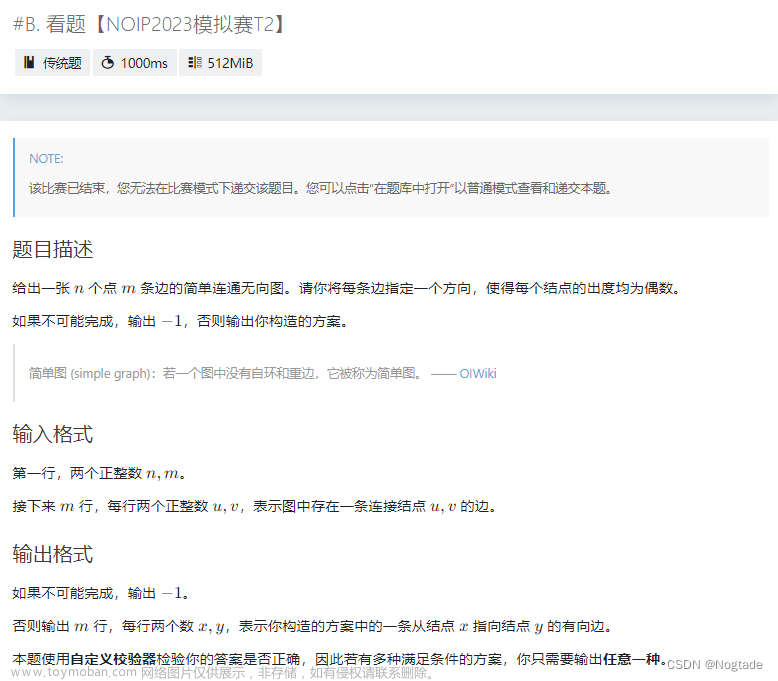
看题：构造

坐飞机:斜率优化DP

抓颓 : 启发式合并 + stl大杂烩

讨厌的线段树

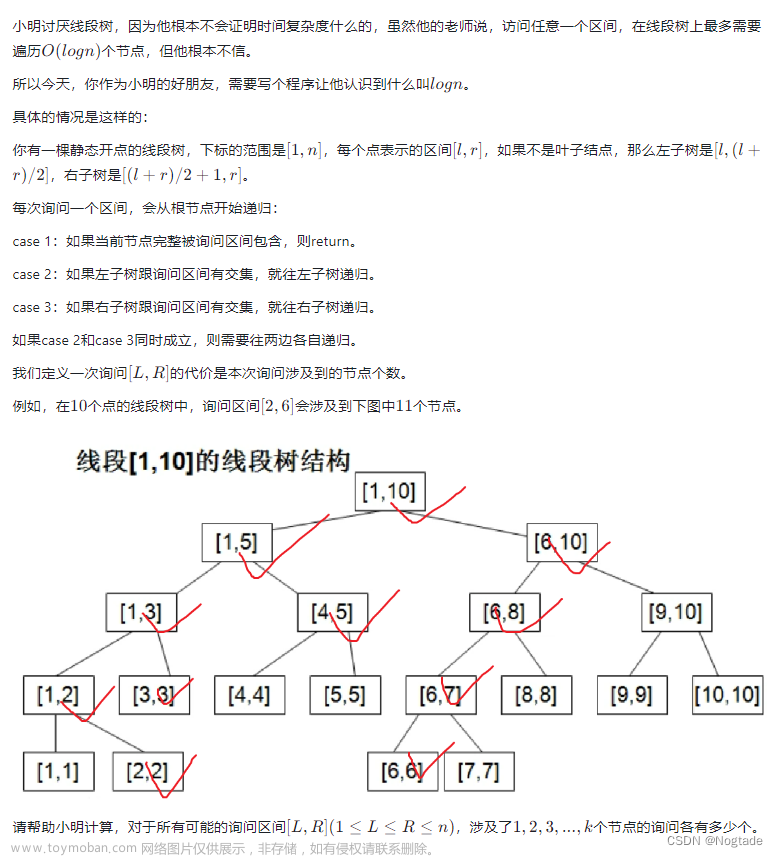
Foo Fighters ：构造

乱搞一：大胆随机化

只需要输出一个S即可，直接随机化，如果不捆绑的话应该可以取得不少的分数

正解:位运算 -> 基本套路 按位考虑

&运算有一个性质 只有(1 & 1) =1 所以最高有效位数低的数字的1的个数的奇偶性不会被较高位1的&运算影响（更自然）

所以我们如果按照位数低向高进行枚举这样可以保证对较高位的运算不会对较低位的答案产生影响

这时候我们发现一个问题，什么是较高位的答案，什么是较低位的答案，明确下个定义:最高位1位置的大小

这样我们将数进行分组，按照最高位进行分组，从低到高枚举，最高位低组的答案一定不会被最高位高组影响

但是仅有这个性质是不够的，会不会较低位的&运算会影响较高位的答案？

但是让我们回想每组的答案跟什么有关系

只跟奇偶性有关系，所以最高位的一个1就可以将这一组分成两组奇数组与偶数组，通过改变最高位1，就可以交换奇数组和偶数组

Hack it! ： 构造

光之剑：计数DP

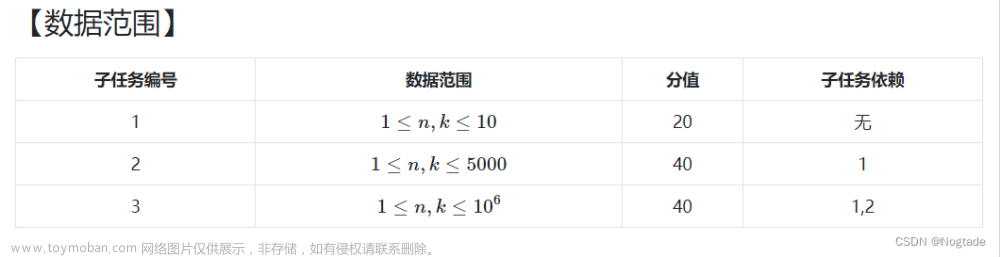
正解:正难则反，取补集

我们从数据入手，一步一步分析，如果\(n,k <= 10\)的话显然直接搜索即可

但是第2档分与爆搜差距过大，所以这档分显然需要我们给出一个\(n^2\)的做法
肯定可以想到这应该是一个计数类的DP，如何设计状态
如果我们正向去做设\(f[i]\)表示以\(i\)为错误答案的贡献
我们发现有两个限制
\(1.保证不是n的数能够有后k个比它小的数\)
\(2.保证它前面没有出现比他大的数 并且没有出现错误答案\)
如果尝试过发现\(f[i]\) 与 \(f[j]\)的联系过小, 细节非常难处理
这时候我们要不断调整状态的设计，将一个大问题转成一个子问题
这时候我们反向思考，如果知道了返回最大值为\(n\)的数量\(res\)，\((n! - res)\)即为答案
那么什么时候会出现返回值为n？
两种情况
1.n个数没有出现返回值
2.让n后面有j个数，且前面的数没有返回值
这时候我们发现第二种情况需要用到第一种情况，那么我们思考如何解决第一种即可
设\(f[x]\)表示\(x\)个数且没有返回值，\(f[j] = j!(j∈[0,k])\)，如何转移?
这时候其实就非常简单了，如果我们将第\(i\)个数放在\(j\)的位置上，我们需要保证前\(j - 1\)个数没有出现返回值，且\(i\)后面不能有\(k\)个数

\(f[i] = f[j-1] * C_{i - 1}^{j-1} * A_{i -j}^{i -j}(j∈[i - k+1,i])\)
这样就能拿到\(60pts\)考虑化简发现随着\(i\)的增加\(1\),\(j\)的左边界少1，右边界大1，将组合数化简\(f[i] = f[j - 1] * (i-1)!/(j-1)!\)这样双指针即可!

/*
发现正着做非常困难， 正难则反
考虑如果n个数的排列最大值能够选到n的情况那么分为两种， 一种是可以选到的， 一种是没有选出来来的 

如果n在前k个则一定能取到， 如果在k + 1个之后

需要保证前k个没有产生最大值 (即没有选出来的)

问题转化为了子问题， 前i个数选不出来  
*/
#include<bits/stdc++.h>
using namespace std;
#define LL long long 
const int MAX = 1e6 + 70;
const int MOD = 1e9 + 7;
int n, k;
LL A[MAX], f[MAX], INV[MAX]; 
LL quick_mi(LL x, LL y) {
	LL xx = x, res = 1;
	while(y) {
		if(y % 2) res = res * xx % MOD;
		xx = xx * xx % MOD;
		y /= 2;
	}  
	return res;
}
LL C(int x, int y) { return (A[x] * INV[y] % MOD * INV[x - y] % MOD); } 
void prework() {
	A[0] = 1;
	for(int i = 1; i <= n; i++) A[i] = (A[i - 1] * i) % MOD;
	for(int i = 0; i <= k; i++) f[i] = A[i]; //随便放 
	for(int i = 0; i <= n; i++) INV[i] = quick_mi(A[i], MOD - 2); //预处理， 少log！！！！！ 
	LL ANS = 0;
	for(int i = k + 1; i >= 2; i--) ANS = (ANS + (f[i - 1] * A[k] % MOD * INV[i - 1] % MOD) ) % MOD;
	f[k + 1] = ANS;
	int l = 1;
	for(int i = k + 2; i <= n; i++) { //前i个位置 
		ANS  = (ANS - (f[l] * A[i - 1 - 1] % MOD * INV[l] % MOD) + MOD) % MOD;
		ANS = ANS * (i - 1) % MOD;
		ANS = ANS + (f[i - 1] * A[i - 1] % MOD * INV[i - 1] % MOD);
		f[i] = ANS;
		l++;
//		for(int j = i; j >= i - k + 1; j--) { //i放的位置
//			f[i] = (f[i] + (f[j - 1] * C(i - 1, j - 1) % MOD * A[i - j] % MOD) )% MOD;	 //可以化简 ****** 
////			printf("j %d f[%d] %lld\n",j, i, f[i]);
//		}
//		printf("f[%d] %lld\n", i, f[i]);
	}
}
int main() {
	freopen("arisu.in","r",stdin);
	freopen("arisu.out","w",stdout);
	scanf("%d%d", &n, &k);
	prework(); //预处理前i个数选不出来的数量 
	LL res = f[n];
//	cout<<f[n]<<endl;
	for(int i = 1; i <= n - k; i++) {
		res = (res + (f[i - 1] * C(n - 1, i - 1) % MOD * A[n - i]) )% MOD;
	}
	cout<<(A[n] - res + MOD) % MOD<<endl;
	return 0;
}

Divide

正解:科技-Stern-Brocot树 法里树

Stern-Brocot树

我们定义\(la = 0,lb=1,ra=1,rb=0\),
令\(x=la+ra,y=lb+rb\),显然得到\(\cfrac{la}{lb}<\cfrac{x}{y}<\cfrac{ra}{rb}\)将得到的\(\cfrac{x}{y}\)重新作为\(la, lb, ra,rb\) 重新进行计算，即可得到上图

性质1 单调性

性质2 SB Tree的所产生的分数都是最简分数

证明

法里树

将右边界改为\(\cfrac{1}{1}\)，所得到的都为<=1的分数

#include<bits/stdc++.h>
using namespace std;
#define LL long long 
#define LB long double
const int MAX = 1e7 + 7;
long double eps = 1e-19;
int fa, fb;
bool flag = 0;
long double val;
int main() {
//	scanf("%d%d", &fa, &fb);
	fa = 1000000000, fb = 1000000000;
	scanf("%Lf", &val);
	int la = 0, lb = 1, ra = 1, rb = 0;
	long double lc = val;
	int ansa = 1, ansb = 0;
	while(1) {
		int x = la + ra, y = lb + rb;
		if(x > fa || y > fb) break;
		LB NOW = ((LB)x / (LB)y);
		if(fabs(NOW - val) < eps) {
			ansa = x, ansb = y;
			break;
		}
		else {
			ansa = x, ansb = y;
			lc = fabs(NOW - val);
			if(NOW - val < 0) {
				la = x, lb = y;
			} else {
				ra = x, rb = y;
			}
		}
	}
	printf("%d %d", ansa, ansb);
	return 0;
}

醒幸：正难则反

相似题目:杭州

简概题意:给定一个图，每次删去边权和最大的森林(即删去的图必须联通且没有环), 求每条边是哪次操作删去的

正解:转化题意, 二分

我们发现每次删去一个最大的森林非常难处理，因为M的数据范围是\(M<=3e5\)需要一个\(log_{m} || \sqrt{m}\)复杂度的算法，非常难维护

观察数据范围\(K*N<=1e7\)也就是说，我们如果可以将删去\(K\)次与\(N\)产生联系即可,删去的图联通没有环，显然是一个树形结构，那么也就是说我们要把\(M\)条边进行分组，生成\(K\)棵树，每一颗树对应了一个删除顺序

现在问题就进行了转换，如何向K个森林里加边，保证没有环且K个森林的边权和从大到小?

对于K个森林边权和从大到小，类Kruskal, 边权从大到小，依次判断往哪个森林加边，如果当前森林中两点不联通，加边，否则，向后判断

到这里我们发现时间复杂度仍然劣，\(M*K*log_{n}\),瓶颈出在哪里?显然是判断往哪个森林里加边，我们显然想要一个\(log\)做法，考虑二分,这样思考，如果对于当前这个森林已经联通，显然会在后边的森林加边，如果不联通，显然会在前面的森林中，感性理解，这样问题就得以解决

#include<bits/stdc++.h>
using namespace std;
#define LL long long 
const int MAX = 2100 + 70;
int n, m, k, ans[MAX * MAX]; 
struct made {
	int fa[1100];
	LL val;
	int Find(int x) {
		if(fa[x] == x) return x;
		return fa[x] = Find(fa[x]);
	}
}P[10002];
struct node { int u, v, val, id; } e[MAX * MAX];
bool mycmp(node X, node Y) { return X.val > Y.val; }
bool mycmp2(node X, node Y) { return X.id < Y.id; }
bool check(int u, int v, int x) {
	if(P[x].Find(u) == P[x].Find(v)) return 0;
	return 1;
}
int add(int x) {
	int l = 1, r = k, res = 0; //查询k个联通块 
	while(l <= r) {
		int mid = (l + r) >> 1;
		if(check(e[x].u, e[x].v, mid)) {
			res = mid;
			r = mid - 1;
		} else  l = mid + 1;
	}
	if(res == 0) return 0;
	int fu = P[res].Find(e[x].u);
	int fv = P[res].Find(e[x].v);
	P[res].fa[fu] = fv;
	return res;
}
int main() {
	scanf("%d%d%d", &n, &m, &k);
	for(int i = 1; i <= m; i++) {
		scanf("%d%d%d", &e[i].u, &e[i].v, &e[i].val); 
		e[i].id = i;
	} 
	for(int i = 1; i <= k; i++) 
		for(int j = 1; j <= n; j++) P[i].fa[j] = j; //初始化 
	sort(e + 1, e + 1 + m, mycmp);
	for(int i = 1; i <= m; i++) {
		int now = add(i); //将第i个边加入连通块 
		ans[e[i].id] = now;
	}
	for(int i = 1; i <= m; i++) printf("%d\n", ans[i]); 
	return 0;
}

ABC321F :退背包

正解:性质题

如果只有\(+\)我们发现就是一道背包题，但是如果有\(-\)操作呢？

但是\(+\)操作的顺序对答案有影响吗?显然是没有的，题目保证不会出现删去没有出现过的数，我们不妨让删去的数放在整个序列的最后一个，倒着删一下即可

//若只有+则序列顺序无所谓 直接背包 
//若有- 则考虑将序列构造成 -的数放在最后一个
//反向-一下即可 
#include<bits/stdc++.h>
using namespace std; 
#define LL long long
const int MAX = 5100;
const int MOD = 998244353;
int q, k, f[MAX + 10];
int main() {
	scanf("%d%d", &q, &k);
	f[0] = 1;
	while(q, q--) {
		char ch; int x;
		scanf("\n%c%d", &ch, &x);
		if(ch == '+') {
			for(int i = MAX; i >= x; i--) {
				f[i] = (f[i - x]  + f[i] ) % MOD; 	
			}
		} else {
			for(int i = x; i <= MAX; i++) {
				f[i] = (f[i] - f[i - x] + MOD) % MOD;
			}
		}
		printf("%d\n", f[k]);
	}
	return 0;
}

农场道路修建 : 问题转化

正解 ：问题转化

题目的大致含义为在\(\frac{N * (N - 1)}{2}\)的点对中增加一条边后的基环树的最大点支配集与原树的大小保持不变

如何思考:
1.我们首先发现在树上增加一条新的边一定不会让最大点支配集的个数变大， 其影响一定只会变小和保持不变

2. 如果在某一种最大点支配集的选择方案中,
(选择点， 选择点) 会让方案变小，
(无， 选择点)，(无， 无)不会让答案变小

显然性质2很好实现，但如果一颗树有多种最大点支配集选择方案该怎么处理, 这时候会出现许多重复

方法一 :

用总数减去(必选点，必选点) 的方案

方法二 :

(无)点： 在某种最大点支配集的选择方案中可以不选的点
用(无)点统计答案， 因为(无)点与其他任意一个点连都可以，但(无)点之间会多连，所以答案为\(Wu_{sum} *(n - 1) -\frac{Wu_{sum}*(Wu_{sum}-1)}{2}\)

选择方法2: 具体方法已经清楚，如何将多种最大点支配集的(无)点选出来?
首先对原树做一遍最大点支配集，从根向下遍历
如果\(bol ==1\)即这个点选择，向下遍历时选择\(son[x]\),\(bol\)修改为0
如果\(bol == 0\)即这个点不选，向下遍历时\(bol\)修改为\(f[][0/1]\)较大的，如果一样同时遍历
如果当前点的\(bol==0\)打上标记，最后统计总数

方法2
#include<bits/stdc++.h>
using namespace std;
#define LL long long 
const int MAX = 3e5 + 70;
int n, tot, head[MAX];
bool flag[MAX];
LL f[MAX][3], ans; // 0 / 1 不选， 选 
int mp[MAX][2];
vector<int> son[MAX];
struct made {
	int l, t;
}edge[MAX * 2];
void add(int u, int v) {
	edge[++tot].l = head[u];
	edge[tot].t = v;
	head[u] = tot;
}
void dfs_pre(int x, int fa) {
//	printf("x %d fa %d\n", x, fa);
	for(int i = head[x]; i; i = edge[i].l) {
		int t = edge[i].t;
		if(t == fa) continue;
		son[x].push_back(t);
		dfs_pre(t, x);
	}
}
void dfs(int x) {
	if(son[x].size() == 0) {
		f[x][1] = 1; f[x][0] = 0;
		return ;
	}
	int len = son[x].size();
	for(int i = 0; i < len; i++) {
		dfs(son[x][i]);
		f[x][1] += f[son[x][i]][0];
		f[x][0] += max(f[son[x][i]][0], f[son[x][i]][1]);
	}
	f[x][1] += 1;
	return ;
}
void dfs_work(int now, int bol) {
	if(mp[now][bol]) return ;
	mp[now][bol] = 1;
	if(bol == 0) flag[now] = 1;
	for(int i = 0; i < son[now].size(); i++) {
		int to = son[now][i];
		if(bol == 0) {
			if(f[to][0] > f[to][1]) dfs_work(to, 0);
			else if(f[to][0] == f[to][1]) {
				dfs_work(to,  0);
				dfs_work(to, 1);	
			}
			else dfs_work(to, 1);
		} else {
			dfs_work(to, 0);
		}
	} 
}
int main() {
	freopen("road.in","r",stdin);
	freopen("road.out","w",stdout);
	scanf("%d", &n);
	for(int i = 1; i < n; i++) {
		int u, v; scanf("%d%d", &u, &v);
		add(u, v); add(v, u);
	}
	dfs_pre(1, 0);
	dfs(1);
	if(f[1][0] > f[1][1]) {
		dfs_work(1,  0);
	} 
	else if(f[1][0] == f[1][1]) {
//		cout<<"ooo";	
		dfs_work(1,  0);
		dfs_work(1,  1);
	}
	else dfs_work(1,  1);
	LL sum1 = 0, sum2 = 0;
	for(int i = 1; i <= n; i++) {
		if(flag[i] == 1) sum1++, ans += (n - 1);
		else sum2++;
	}
//	cout<<ans<<" "<<sum1<<endl;
	cout<<ans - ((sum1 - 1) * sum1 / 2)<<endl;
	return 0;
} 

密码锁：优化DP

25pts:DP

首先排除贪心的思路， 对于前三挡我们希望拥有一个带常数的\(N*Q\)的算法，考虑设计DP状态，\(f[i][j]\)表示填充前\(i\)位，第\(i\)为\(j\)的最小代价
时间复杂度\(N*Q*26*26\) 勉强跑过?

55pts：区间DP+线段树优化

发现上面的状态没有拓展性，希望转化状态，然后发现修改先后顺序无所为，只需要让两个相邻区间合并时满足\(Lr <= Rl\)即可，考虑区间DP\(f[L][R][l][r]\)表示左右端点为\(L,R\)左右填充\(l, r\)的最小代价
考虑简化状态:我们发现设定的DP状态中很多都不必要存在，修改符合结合率，考虑线段树倍增优化这个状态

#include<bits/stdc++.h> // 25  感觉可以优化(DP 区间可合并， 线段树) 
using namespace std;
#define LL long long 
const int MAX = 1e5 + 70;
int fp[MAX][30]; 
int q, len;
char ch[MAX];
int cha(int x, int y) { //x  -> y的最小花费  
	if(x < y) return y - x;
	else return x - y;
}
struct SegmentTree {
	int l, r;
	int f[6][6]; //左 端点， 右端点分别填啥 
	#define l(x) tree[x].l
	#define r(x) tree[x].r
	#define t(x) tree[x]
}tree[MAX * 4];
void update(int p) {
	memset(t(p).f, 0x3f, sizeof(t(p).f)); 
	for(int ll = 1; ll <= 5; ll++) {
		for(int lr = ll; lr <= 5; lr++) {
			for(int rl = lr; rl <= 5; rl++) {
				for(int rr = rl; rr <= 5; rr++) {
					t(p).f[ll][rr] = min(t(p).f[ll][rr], t(2 * p).f[ll][lr] + t(2 * p + 1).f[rl][rr]); 
//					printf("p %d l %d r %d f[%d][%d] %d\n",p, l(p), r(p), ll, rr, t(p).f[ll][rr]);
				}
			}
		}
	}
	return ;
}
void build(int p, int l, int r) {
	memset(t(p).f, 0x3f, sizeof(t(p).f));
	l(p) = l, r(p) = r;
	if(l == r) {
		int val = (int)(ch[l] - 'a' + 1);
		memset(t(p).f, 0x3f, sizeof(t(p).f));
		for(int i = 1; i <= 5; i++) {
			t(p).f[i][i] = cha(val, i);
//			printf("l %d r %d .f[%d][%d] %d\n", l, r, i, i, t(p).f[i][i]);	
		} 
		return ;
	}
	int mid = (l + r) >> 1;
	build(2 * p, l, mid);
	build(2 * p + 1, mid + 1, r);
	update(p);
}
void change(int p, int l, int r, int val) {
	if(l(p) == r(p)) {
		memset(t(p).f, 0x3f, sizeof(t(p).f));
		for(int i = 1; i <= 5; i++) {
			t(p).f[i][i] = cha(val, i);
//			printf("l %d r %d .f[%d][%d] %d val %d \n", l, r, i, i, t(p).f[i][i], val);				
		}
		return ;
	}
	int mid = (l(p) + r(p)) / 2;
	if(l <= mid) change(2 * p, l, r, val);
	if(r > mid) change(2 * p + 1, l, r, val);
	update(p);
	return ;
}
int GET_ANS() {
	int ans = 0x3f3f3f3f;
	for(int i = 1; i <= 5; i++) {
		for(int j = i; j <= 5; j++) {
//			printf("f[%d][%d] %d\n", i, j, t(1).f[i][j]);
			ans = min(ans, t(1).f[i][j]);
		}
	}
	return ans;
}
void prework() {
	memset(fp, 0x3f, sizeof(fp));
	for(int i = 1; i <= 26; i++) {
		fp[1][i] = cha(int(ch[1] - 'a' + 1), i); 
	}
	for(int i = 2; i <= len; i++) {
		for(int j = 1; j <= 26; j++) { //当前这位填啥 
			for(int k = 1; k <= j; k++) {
				fp[i][j] = min(fp[i][j], fp[i - 1][k] + cha((int)(ch[i] - 'a' + 1), j)); 
			}
		}
	}
}
int main() {
	freopen("lock.in","r",stdin);
	freopen("lock.out","w", stdout);
	scanf("%s", ch + 1); len = strlen(ch + 1);
	build(1, 1, len);
	scanf("%d", &q);
	if(q <= 10) {
		prework();	
		int ans = 0x3f3f3f3f;
		for(int i = 1; i <= 26; i++) {
			ans = min(ans, fp[len][i]);
		}
		cout<<ans<<endl;
		for(int i = 1; i <= q; i++) {
			int id; cin>>id;
			char chr; cin>>chr;
			int ans = 0x3f3f3f3f;
			ch[id] = chr;
			int now = int(chr - 'a') + 1;
			prework();
			for(int j = 1; j <= 26; j++) {
				ans = min(ans, fp[len][j]) ;
			}
			cout<<ans<<endl;
		}
		return 0;
	}
	int ans = GET_ANS();
	cout<<ans<<endl;
	for(int i = 1; i <= q; i++) {
		int id; cin>>id;
		char chr; cin>>chr;
		int now = int(chr - 'a') + 1;
//		cout<<"id "<<id<<" now "<<now<<endl;
		change(1, id, id, now);
		int ans = GET_ANS();
		cout<<ans<<endl;
	}
	return 0;
}

100pts：问题转化+性质

在全部数据中如果左右端点都有26种选择，那么\(26 * 26*26*26\)的巨大常数直接爆炸

发现问题可以转化为将序列进行26次只含有(0/1)的最小代价之和，对于设\(i\)∈\([a,z]\)分别将序列中的大于等于i的设为1，小于i的设为0，将代价累加起来即为答案
为什么这样转化问题是正确且保证最小 ？(不是很懂)
证明:

任务四的方法对于26的矩阵可能比较慢，设b(S,i)为一个长度为n的01串，第j个位置的值表示[S_j>=i]，也就是当S_j>=i,该位置是1，否则是0。
那么对于b(S,i)，可以当作只有a,b两种字符的问题的求解。
令F(s)为s串的答案，下面证明：\(\sum_{i='a'}^{'z'}F(b(S,i))=F(S)\)
对于原串的一种最优解S',考虑对于一个位置j，有|S_j-S'j|个i在j位置是不同的，也就是有这么多i在该位置是有代价的。因此，对于任意一种最优解都有一种代价相等的将所有的b(S,i)变为b(S',i)的方案。因此\(\sum_{i='a'}^{'z'}F(b(S,i))\le F(S)\)
考虑对于每个i，b(S,i)的最佳答案。设\(Z_i\)为该答案中0的个数。
如果\(Z_i\)单调递增，那么把i号字符放在\([Z_i,Z_i+1)\)就能构造一种恰好答案相等的原串方案。
如果\(Z_i\)不单调递增，假设\(Z_i>Z_{i+1}\)，那么交换i和i+1的方案不会使答案更劣，因为对于每个位置，b(S,i)和b(S,i+1)的对位情况只能有(1,0),(0,0),(1,1)。因此如果出现\(Z_i>Z_{i+1}\)，那么对位就出现了(0,1),一定是可以交换的。那么通过交换，可以得到一个\(Z_i\)单调递增的方案。那么也就说明了
\(\sum_{i='a'}^{'z'}F(b(S,i))\ge F(S)\)
因此
\(\sum_{i='a'}^{'z'}F(b(S,i))= F(S)\)
对于每个01串分开做动态dp，要比26大小的矩阵做动态dp要更快，即可得到满分**

#include<bits/stdc++.h> 
using namespace std;
#define LL long long 
const int MAX = 1e5 + 70;
int fp[MAX][30]; 
int q, len;
char ch[MAX];
int cha(int x, int y) { //x  -> y的最小花费  
	if(x < y) return y - x;
	else return x - y;
}
struct SegmentTree {
	int l, r;
	int f[2][2]; //左 端点， 右端点分别填啥 
	#define l(x,y) tree[x][y].l
	#define r(x,y) tree[x][y].r
	#define t(x,y) tree[x][y]
}tree[30][MAX * 4];
void update(int p) {
	for(int i = 1; i <= 26; i++) memset(t(i, p).f, 0x3f, sizeof(t(i, p).f)); 
	for(int ro = 1; ro <= 26; ro++) {
		for(int ll = 0; ll <= 1; ll++) {
			for(int lr = ll; lr <= 1; lr++) {
				for(int rl = lr; rl <= 1; rl++) {
					for(int rr = rl ; rr <= 1; rr++) {
						t(ro, p).f[ll][rr] = min(t(ro, p).f[ll][rr], t(ro, 2 * p).f[ll][lr] + t(ro, 2 * p + 1).f[rl][rr]);
					}
				}
			}
		}
	}
	return ;
}
void build(int p, int l, int r) {
	for(int i = 1; i <= 26; i++) memset(t(i, p).f, 0x3f, sizeof(t(i, p).f));
	for(int i = 1; i <= 26; i++) l(i, p) = l, r(i, p) = r;
	if(l == r) {
		for(int i = 1; i <= 26; i++) {
			memset(t(i, p).f, 0x3f, sizeof(t(i, p).f));
			int val = (ch[l] - 'a' + 1 >= i ? 1 : 0);
			for(int j = 0; j <= 1; j++) t(i, p).f[j][j] = cha(val, j);
		}
		return ;
	}
	int mid = (l + r) >> 1;
	build(2 * p, l, mid);
	build(2 * p + 1, mid + 1, r);
	update(p);
}
void change(int p, int l, int r, int val) {
	if(l(1, p) == r(1, p)) {
		for(int i = 1; i <= 26; i++) {
			memset(t(i, p).f, 0x3f, sizeof(t(i, p).f));
			int V = (val >= i ? 1 : 0);
			for(int j = 0; j <= 1; j++) t(i, p).f[j][j] = cha(V, j);			
		}
		return ;
	}
	int mid = (l(1, p) + r(1, p)) / 2;
	if(l <= mid) change(2 * p, l, r, val);
	if(r > mid) change(2 * p + 1, l, r, val);
	update(p);
	return ;
}
int GET_ANS() {
	int ans = 0;
	for(int i = 1; i <= 26; i++) {
		int sum = 0x3f3f3f3f;
		for(int l = 0; l <= 1; l++) {
			for(int r = l; r <= 1; r++) 
				sum = min(sum, t(i, 1).f[l][r]);
		}
		ans += sum;
	}
	return ans;
}
int main() {
	freopen("lock.in","r",stdin);
	freopen("lock.out","w", stdout);
	scanf("%s", ch + 1); len = strlen(ch + 1);
	build(1, 1, len);
	scanf("%d", &q);
	int ans = GET_ANS();
	cout<<ans<<endl;
	for(int i = 1; i <= q; i++) {
		int id; cin>>id;
		char chr; cin>>chr;
		int now = int(chr - 'a') + 1;
		change(1, id, id, now);
		int ans = GET_ANS();
		cout<<ans<<endl;
	}
	return 0;
}

魔法是变化之神

60pts:背包,求补集

将答案分成两部分，第一部分为固定答案，第二部分为减少的总数，将\(SIZ[]\)看做体积，将减小量看做价值，背包即可拿到60pts

#include<bits/stdc++.h>
using namespace std;
#define LL long long 
const int MAX = 110000;
int n, m, ANS, siz[MAX], fat[MAX];
int tot, head[MAX], f[MAX];
struct made {
	int l, t, val;
}edge[MAX *2], e[MAX *2];
void add(int u, int v, int val) {
	edge[++tot].l = head[u];
	edge[tot].t = v;
	edge[tot].val = val;
	head[u] = tot;
}
void dfs_pre(int x, int fa) {
	fat[x] = fa;
	siz[x] = 1;
	for(int i = head[x]; i; i = edge[i].l) {
		int t = edge[i].t;
		if(t == fa) continue;
		dfs_pre(t, x);
		siz[x] += siz[t];
	}
}
int main() {
	freopen("tree.in","r",stdin);
	freopen("tree.out","w",stdout);
	scanf("%d%d", &n, &m);
	for(int i = 1; i < n; i++) {
		int u, v, val; scanf("%d%d%d", &u, &v, &val);
		e[i].l = u, e[i].t = v, e[i].val = val;
		add(u, v, val); add(v, u, val);
	}
	dfs_pre(1, 0);
	for(int i = 1; i <= n; i++) {
		int U = e[i].l;
		if(fat[U] != e[i].t) U = e[i].t;		
		ANS += ((n - siz[U]) * (siz[U]) * e[i].val);
		for(int j = m; j >= siz[U]; j--) {
			f[j] = max(f[j], f[j - siz[U]] + (n - siz[U]) * (siz[U] * e[i].val));
		}
	}
	cout<<ANS - f[m];
	return 0;
}

100pts：考虑随机数据

因为数据随机，所以SIZ的期望个数有\(log_{n}\)中，因为边的价值最多为5，将价值和\(SIZ\)相同的合并在一起，多重背包即可

#include<bits/stdc++.h>
using namespace std;
#define LL long long 
const int MAX = 110000;
int n, m;
LL ANS; 
int siz[MAX], fat[MAX];
int tot, head[MAX];
LL f[MAX];
int cnt[MAX][10];
struct made {
	int l, t, val;
}edge[MAX *2], e[MAX *2];
void add(int u, int v, int val) {
	edge[++tot].l = head[u];
	edge[tot].t = v;
	edge[tot].val = val;
	head[u] = tot;
}
void dfs_pre(int x, int fa) {
	fat[x] = fa;
	siz[x] = 1;
	for(int i = head[x]; i; i = edge[i].l) {
		int t = edge[i].t;
		if(t == fa) continue;
		dfs_pre(t, x);
		siz[x] += siz[t];
	}
}
void work() {
	for(int i = 1; i < n; i++) {
		int U = e[i].l;
		if(fat[U] != e[i].t) U = e[i].t;		
		ANS += ((LL)(n - siz[U]) * (LL)(siz[U]) * (LL)e[i].val);
		cnt[siz[U]][e[i].val]++; 
	}
}
inline int read() {
	int x = 0, f = 1;
	char c = getchar();
	while(c < '0' || c > '9') { if(c == '-') f = -1; c = getchar(); }
	while(c >= '0' && c <= '9') { x = (x * 10 + f * (int)(c - '0')); c = getchar(); }
	return x;
}
int main() {
	freopen("tree.in","r",stdin);
	freopen("tree.out","w",stdout);
	n = read(), m = read();
//	cout<<n<<endl;
	for(int i = 1; i < n; i++) {
		int u, v, val; 
		u = read(), v = read(), val = read();
		e[i].l = u, e[i].t = v, e[i].val = val;
		add(u, v, val); add(v, u, val);
	}
	dfs_pre(1, 0);
	work();
	for(int j = 100000; j >= 1; j--) {
		for(int k = 5; k >= 1; k--) {
			if(cnt[j][k] == 0) continue;
			int C2 = 1;
			while(C2 <= cnt[j][k]) {
				LL W = C2 * (LL)j, val = (LL)C2 * k * j * (n - j);
				for(int i = m; i >= W; i--) 
					f[i] = max(f[i], f[i - W] + val);
				cnt[j][k] -= C2;
				C2 *= 2;
			}
			if(cnt[j][k]) {
				LL W = cnt[j][k] * j, val = (LL)cnt[j][k] * k * j * (n - j);
				for(int i = m; i >= W; i--) 
					f[i] = max(f[i], f[i - W] + val);
			}
		}
		
	}
	cout<<ANS - f[m];
	return 0;
}

奶牛的数学题:单位贡献

正解

看题 看到数据范围就应该想到这题是一道数学题，或者(矩阵乘法)， 但显然无法写出线性递推式，所以应该往数学上思考
1.如果一个数的\(f(x) = i\), 则\(x\)最小为\(lcm(1~i)\), 可得\(f(x) <= 50\)
2.将\(num[i] * i = \sum _{i = 1}^{i<=50}\sum_{j=i}^{j<=50} num[j]\)

3. 所以题目转化为了对于每一个\(i \in50\) \(f(x) \ge i\)的个数， 如何计算个数，通过1可得，若\(f(x) \ge i\)则\(x\)必须为\(lcm\left \{ 1,2,3...(i-1) \right \}\)的倍数，计算即可

#include<bits/stdc++.h> //将贡献拆为单位贡献 
using namespace std;
#define LL long long 
const int MAX = 1e4 + 70;
const int MOD = 1e9 + 7;
int main() {
	freopen("math.in","r",stdin);
	freopen("math.out","w",stdout);
	int t; scanf("%d", &t);
	while(t, t--) {
		LL n; scanf("%lld", &n);
		LL SUM = 1, ans = n % MOD;
		for(int i = 2; i <= 50; i++) {
			if(SUM > n) break;
			ans = (ans + (n / SUM)) % MOD;
			SUM = SUM * i / __gcd(SUM, (LL)i); 
		}
		cout<<ans<<endl;
	}
	return 0;
}

路遇矩阵

1.20pts的部分分是一个很好的切入点，我们发现只有行和只有列顺序无关，贪心的选一定最优

2.但是行和列放在一起，肯定不能贪心，因为如果选的次数\(k\)非常大，行数小，列数恰好为\(k\),那么选\(k\)列反而最优
如何解决? 枚举选多少个行，多少个列即可

//1. 删除顺序与答案统计无关，答案只与选择有关 
//2. 只删行与只删列满足贪心性质 
#include<bits/stdc++.h> 
using namespace std;
#define LL long long 
const int MAX = 1e3 + 70;
int n, m, k, p;
int a[MAX][MAX];
LL ans = 0, ANS = -1e18, H[1100000], L[1100000];
multiset<LL> h, l;
int main() {
	freopen("matrix.in","r",stdin);
	freopen("matrix.out","w",stdout);
	scanf("%d%d%d%d", &n, &m, &k, &p);
	for(int i = 1; i <= n; i++)
		for(int j = 1; j <= m; j++)
			scanf("%d", &a[i][j]);
	for(int i = 1; i <= n; i++) {
		LL sum = 0;
		for(int j = 1; j <= m; j++) sum += a[i][j];
		h.insert(sum);
	}
	for(int j = 1; j <= m; j++) {
		LL sum = 0;
		for(int i = 1; i <= n; i++) sum += a[i][j];
		l.insert(sum);
	}
	LL sum = 0;
	for(int i = 0; i <= k; i++) { //控制删i个行
		H[i] = sum;
		sum += *h.rbegin();
	 	LL NOW = *h.rbegin();
		set<LL>::iterator it = h.end();
	 	it--;
	 	h.erase(it);
	 	h.insert(NOW - (LL)p * m);
	}
	sum = 0;
	for(int i = 0; i <= k; i++) {
		L[i] = sum;
		sum += *l.rbegin();
	 	LL NOW = *l.rbegin();
		set<LL>::iterator it = l.end();
	 	it--;
	 	l.erase(it);
	 	l.insert(NOW - (1LL * p * n));
	}
	for(int i = 0; i <= k; i++) {
		ANS = max(ANS, L[i] + (H[k - i] - (1LL * p * i * (k - i))));
	}
	cout<<ANS<<endl;
	return 0;
}

奶牛的括号匹配:状压

一眼状压，但是如何设计状态呢?
首先套路的设定\(f(i)\)表示选定集合\(i\)所能产生的最大前缀匹配个数

但是若将\(j\)加入集合\(i\)必须满足当前的\(i\)集合的最大方案是可以拓展的

那我们规定\(f(i)\)表示 \(i\) 集合的最大答案，且当前的排列顺序保证可以拓展 即 \((\) 的个数 始终\(\ge\) \()\)

那么如何计算\(j\)对于集合\(i\)的贡献，如果集合\(i\)的剩余 \({\color{Green} {\LARGE （} }\) 括号的个数为 \(k\), 那么\(j\)所能贡献的数量即为\(cnt_jk\)表示第\(j\)个串前缀\({\color{Green} {\LARGE ）} }\)个数为\(k\)的数量位置

//状压DP， 状态设计
// f[i] 表示集合i最大答案， 转移
// 往i中添加新的字符串j， 考虑j的贡献 
// 若集合i匹配完仍剩OP个( 计算j的贡献 
#include<bits/stdc++.h>
using namespace std;
#define LL long long 
const int MAX = 22;
const int oo = 114514123;
int n, ans, cnt[MAX][410000]; //表示第i个串，出现j的个数 
int f[(1 << MAX)];
int maxx[MAX], END[410000]; //表示第j个的最大的)  和 每个串最后的值 
string s[MAX];
int num[(1 << MAX)]; //表示集合i的剩余(个数 
void prework(int id, string S) {
	int sum = 0;
	maxx[id] = -oo;
	for(int i = 0; i < S.size(); i++) {
		if(S[i] == '(') sum--;
		else sum++;
		maxx[id] = max(maxx[id], sum); 
		if(sum >= maxx[id]) cnt[id][sum]++;
	}
	END[id] = sum;
}
int main() {
	freopen("seq.in","r",stdin);
	freopen("seq.out","w",stdout);
	scanf("%d", &n);
	for(int i = 0; i < n; i++) cin>>s[i]; // 第i个串
	for(int i = 0; i < n; i++) prework(i, s[i]); //预处理第i个串的信息 
	for(int i = 0; i <= (1 << 21) - 1; i++) f[i] = -oo;
	f[0] = 0;
	for(int i = 0; i <= (1 << n) - 1; i++) { //枚举 i集合
		for(int j = 0; j < n; j++) { //选择第j个填加 
			if( (i >> j ) & 1) continue;
			if(num[i] >= maxx[j]) { //说明可以更新下一个f集合 
				f[i | (1 << j)] = max(f[i | (1 << j)], f[i] + cnt[j][num[i]]);
				num[i | (1 << j)] = num[i] - END[j];
				ans = max(ans, f[i | (1 << j)]);
			} else { //不可以更新f集合但是可以统计答案 
				ans = max(ans , f[i] + cnt[j][num[i]]);				
				num[i | (1 << j)] = num[i] - END[j];
			}	
		}
	} 
	cout<<ans<<endl;
	return 0;
} 	

润不掉了：转化点对问题

一步一步分析

20pts:爆搜，但是不好打

40pts

我们分析，如果对于当前的根为\(root\)

对于\(root\)的若干子树，什么子树需要贡献1(被一个点看守)的答案呢?

那么应该是子树\(i\)中的叶节点到\(ro_i\)的最小距离\(\le\)\(dis(x,roi)\),

我们预处理叶子节点到其他点的最小距离，枚举每一个点为根，向下递归答案即可

#include<bits/stdc++.h>
using namespace std;
#define LL long long 
const int MAX = 7e4 + 70;
int n, tot, head[MAX], du[MAX], len[MAX];
vector<int> son[MAX]; // 
queue<int> q;
void BFS() {
	while(!q.empty()) {
		int now = q.front(); q.pop();
		for(auto y : son[now]) {
			if(len[y] > len[now] + 1) {
				len[y] = len[now] + 1;
				q.push(y);
			}
		}
	}
}
int dfs(int now, int fa, int dis) {
	if(len[now] <= dis) return 1;
	if(du[now] == 1) return 1;
	int sum = 0;
	for(auto y : son[now]) {
		if(y == fa) continue;
		sum = sum + dfs(y, now, dis + 1);
	} 
	return sum;
}
int main() {
	freopen("run.in","r",stdin);
	freopen("run.out","w",stdout);
	scanf("%d", &n);
	for(int i = 1; i < n; i++) {
		int u, v; scanf("%d%d", &u, &v);
		son[u].push_back(v);
		son[v].push_back(u); //存边 
		du[u] += 1; du[v] += 1;
	} 
	memset(len, 0x3f, sizeof(len));
	for(int i = 1; i <= n; i++) if(du[i] == 1) len[i] = 0, q.push(i);
	BFS() ; // 处理 
	for(int i = 1; i <= n; i++) {
		int ans = dfs(i, 0, 0) ; // 第i 个点向子树跑 
		printf("%d\n", ans);
	}
	return 0;
}

100pts 子树贡献转化

我们想，40pts没有拓展性，因为无论怎样，枚举根的操作已经限制了整个算法，如何拓展呢?

我们想对于\(x\)有贡献子树的每个点都满足\(g(i) \le dis(i,x))\),

如果我们将整棵子树的贡献设为1的话，那么就是计算点对问题，显然淀粉质就可以了

下面思考树的子树的性质

\(\sum{du}=2siz-1\)
变形
\(\sum{du}-2siz=1\)
\(\sum{du-2}=1\)
所以我们将每个点的val设为\(du -2\)对于点\(x\)的ans即为满足

\(g(i)\le dis(i,x)\)的所有点的val之和
若\(ro\)为分治重心,统计过\(ro\)的点的答案
则\(g(i)\le dis(ro,i)+dis(ro,x)\)
则\(g(i)-dis(ro,i)<=dis(ro,x)\)
树状数组维护

#include<bits/stdc++.h>
using namespace std;
#define LL long long 
const int MAX = 7e4 + 70;
int n, tot, head[MAX], du[MAX], len[MAX], val[MAX];
bool v[MAX];  
vector<int> son[MAX]; // 
queue<int> q;
int ro, maxx_tr, f[MAX], dis[MAX], siz[MAX], g[MAX], NUM; 
int tree[MAX << 1], ans[MAX]; 
int lowbit(int x) { return x & (-x); }
void add(int x, int val) { for(int i = x; i <= 2 * n; i += lowbit(i)) tree[i] += val; } 
int Find(int x) { int sum = 0; for(int i = x; i; i -= lowbit(i)) sum += tree[i]; return sum; }
void get_root(int x, int fa) { //求重心 
	siz[x] = 1, f[x] = 0;
	for(auto To : son[x]) {
		if(To == fa || v[To]) continue;
		get_root(To, x);
		siz[x] += siz[To];
		f[x] = max(f[x], siz[To]);
	}
	f[x] = max(f[x], NUM - siz[x]);
	if(f[x] < maxx_tr) {
		maxx_tr = f[x];
		ro = x;
	}
}
void Clear() { maxx_tr = n + 1; }
void get_size(int x, int fa) {
	siz[x] = 1;
	for(auto y : son[x]) {
		if(y == fa || v[y]) continue;
		get_size(y, x);
		siz[x] += siz[y];
	}
}
void calc(int x, int fa) {
	dis[x] = dis[fa] + 1;
	ans[x] = ans[x] + Find(dis[x] + n); //加上n的偏移量 
	for(auto y : son[x]) {
		if(y == fa || v[y]) continue;
		calc(y, x); 
	}
}
void change(int x, int fa, int zf) {
	add(n + g[x] - dis[x], zf * val[x]);
	for(auto y : son[x]) {
		if(y == fa || v[y]) continue;
		change(y, x, zf);
	}
}
void work(int x, int id) {
	dis[x] = 0;
	if(id == 1) add(g[x] + n, val[x]); //端点有x，x的影响 
	for(auto y : son[x]) {
		if(v[y]) continue;		
		calc(y, x); //统计当前这颗子树的答案 
		change(y, x, 1); //将影响加上去 
	}
	if(id == 1) ans[x] += Find(n);//计算端点值 
	
	for(auto y : son[x]) { //倒着做一次 
		if(v[y]) continue;
		change(y, x, -1); 
	}
	if(id == 1) add(g[x] + n, -val[x]); 
}
void slove(int x) {  //计算过x的点对之间的答案 
	v[x] = 1;
	work(x, 1); 
	reverse(son[x].begin(), son[x].end());
	work(x, 2);
	for(auto y :son[x]) {
		if(v[y]) continue;
		Clear();
		get_size(y, x); 
		NUM = siz[y];
		get_root(y, x);  //分治下去 
		slove(ro); 
	}
}
void BFS() {
	while(!q.empty()) {
		int now = q.front(); q.pop();
		for(auto y : son[now]) {
			if(g[y] > g[now] + 1) {
				g[y] = g[now] + 1;
				q.push(y);
			}
		}
	}
}
int main() {
//	freopen("run.in","r",stdin);
//	freopen("run.out","w",stdout);
	scanf("%d", &n);
	for(int i = 1; i < n; i++) {
		int u, v; scanf("%d%d", &u, &v);
		son[u].push_back(v);
		son[v].push_back(u); 
		du[u] += 1; du[v] += 1;
	} 
	memset(g, 0x3f, sizeof(g));
	for(int i = 1; i <= n; i++) if(du[i] == 1) q.push(i), g[i] = 0;  //多源最短路 
	BFS();
	for(int i = 1; i <= n; i++) val[i] = 2 - du[i]; //问题转化， 
	Clear();
	get_size(1, 0);
	NUM = siz[1];
	get_root(1, 0); 
	slove(ro);
	for(int i = 1; i <= n; i++) {
		if(du[i] == 1) printf("1\n");
		else printf("%d\n", ans[i]);
	}
	return 0;
}

美好的查询:神奇主席树

80pts：分块+并查集

不是很懂，先锅着

100pts:神奇主席树，多看看

数据范围为\(5e5\)，也就是说我们希望得到一个\(log\)常数级别的程序，如何思考?

首先发现只有区间修改与区间查询，而修改是将某一个范围的固定值修改,且值不会大于\(5e5\)

如果我们在一颗线段树上做的话，点权值不同无法统计且时间复杂度不能保证，我们按值分组

构建\(5e5\)棵线段树，每一颗线段树对应着一个值，初始将\(ro[0]\)的树的每个节点都设为\(1\),如果出现将某段区间加\(1\)操作，将\(ro[x+1]\)区间指向\(ro[x]\)的区间，但是我们会发现一个问题，细看下面的错误操作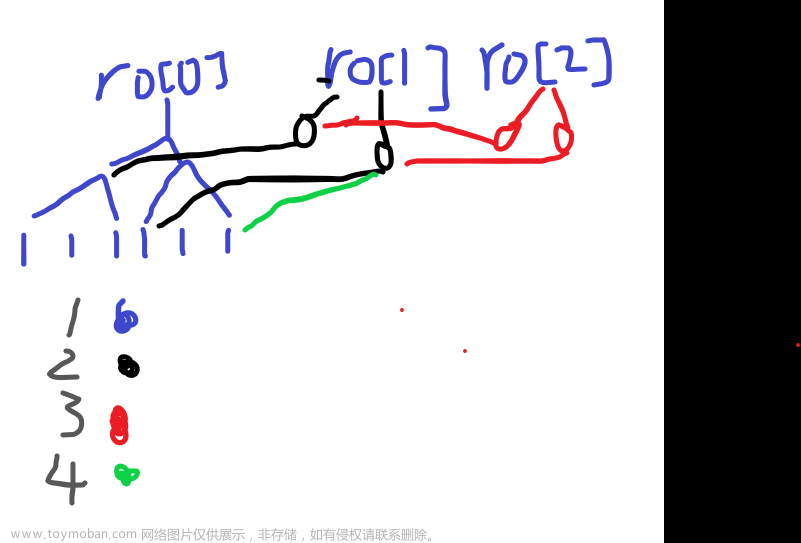

如果我们按照上述数据依次操作，我们发现原本不属于\(ro[2]\)的节点却被归到的\(ro[2]\),也就是说我们对当前某一个值的修改会影响到下一个值，貌似很难处理，但实际很简单，重新开一颗树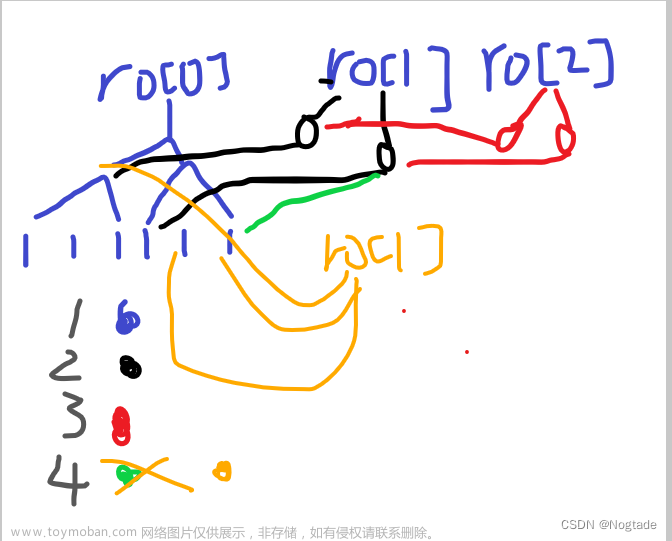

这样就很好解决了这个问题!为保证空间，采用动态开点

总结不出来什么啊

//在线， 5e5考虑log做法，值域主席树 可维护，二分查最大值，复杂度n*log^2 
#include<bits/stdc++.h>
using namespace std;
#define LL long long 
const int MAX = 5e5 + 80;
const int logMAX = 170;
int n, q, ro[MAX], tot;
struct made { int id, l, r, x; }ask[MAX];
struct SegmentTree {
	int lson, rson, sum;
	#define lson(x) tree[x].lson
	#define rson(x) tree[x].rson
	#define sum(x) tree[x].sum
}tree[MAX * logMAX];
int build() { return ++tot; }
void update(int p) { sum(p) = sum(lson(p)) + sum(rson(p)); }
void pre_build_0(int p, int l, int r) {
	if(l == r) {
		sum(p) = 1;
		return ;
	}  
	lson(p) = build();
	rson(p) = build();
	int mid = (l + r) >> 1;
	pre_build_0(lson(p), l, mid);
	pre_build_0(rson(p), mid + 1, r);
	update(p);
}
int copy(int p, int q, int L, int R, int l, int r) {
	if(L >= l && R <= r) { return p; } //为什么一定正确，反证法
	if(p == 0) return p;
	int now = build(); tree[now] = tree[q]; //复制
	int mid = (L + R) >> 1;
	if(mid >= l) lson(now) = copy(lson(p), lson(now), L, mid, l, r);
	if(r > mid) rson(now) = copy(rson(p), rson(now), mid + 1, R, l, r);
	update(now);
	return now; 
}
int qurry(int p, int L, int R, int l, int r) {
	if(L >= l && R <= r) {
		return sum(p);
	}
	int sum = 0;
	int mid = (L + R) >> 1;
	if(l <= mid) sum = sum + qurry(lson(p), L, mid, l, r);
	if(r > mid) sum = sum + qurry(rson(p), mid + 1, R, l, r);
	return sum;  
}
int Find(int L, int R) {
	int l = 0, r = 5e5, ans = 0;
	while(l <= r) {
		int mid = (l + r) >> 1;
		if(qurry(ro[mid],1, n, L, R)) {		
			ans = mid;
			l = mid + 1;
		} else {
			r = mid - 1;
		}
	}
	return ans;
}
int main() {
	freopen("Innocent.in","r",stdin);
	freopen("Innocent.out","w",stdout);
	scanf("%d%d", &n, &q);
	ro[0] = build();
	pre_build_0(ro[0], 1, n); //建0的树 
	for(int i = 1; i <= q; i++) {
		int op; scanf("%d", &ask[i].id);
		if(ask[i].id == 1) scanf("%d%d%d", &ask[i].l, &ask[i].r, &ask[i].x);
		if(ask[i].id == 2) scanf("%d%d",&ask[i].l, &ask[i].r);
	}
	for(int i = 1; i <= q; i++) {
		if(ask[i].id == 1) {
			int now = copy(ro[ask[i].x], ro[ask[i].x + 1], 1, n, ask[i].l, ask[i].r); //保证空间为log 
			ro[ask[i].x + 1] = now;
		} 
		else {
			int ans = Find(ask[i].l, ask[i].r);
			printf("%d\n", ans);
		}
	}
	return 0;
}

新涂色游戏:操作反做

回头看这道题其实非常简单

对于涂色,整行或整列，则最后一定有一整行或一整列为一个颜色，反着做，再将操作reverse就可以了

//正着做不好做，反着删 
#include<bits/stdc++.h>
using namespace std;
#define LL long long 
#define PII pair<int, int>
const int MAX = 1100;
int n, a[MAX][MAX], tot;
bool can[2 * MAX];
int num[2 * MAX][2 * MAX], kind[2 * MAX];
PII ans[2 * MAX];
void work(int id) {
	if(id <= n) {
		int co;
		for(int i = 1; i <= n; i++) {
			if(a[id][i] != 0 && a[id][i] != -1) {
				co = a[id][i];
				num[n + i][a[id][i]]--;
				if(num[n + i][a[id][i]] == 0) kind[n + i] -= 1;
				a[id][i] = 0;
			}
		}
		ans[++tot] = {(PII){id, co}};
	} else {
		int co;
		id = (id % n == 0) ? (n) : (id % n);
		for(int i = 1; i <= n; i++) {
			if(a[i][id] != 0 && a[i][id] != -1) {
				co = a[i][id];
				num[i][a[i][id]]--;
				if(num[i][a[i][id]] == 0) kind[i] -= 1;
				a[i][id] = 0;
			}
		}
		ans[++tot] = {(PII){id + n, co}};
	}
}
int main() {
	freopen("game.in","r",stdin);
	scanf("%d", &n);
	for(int i = 1; i <= n; i++) 
		for(int j = 1; j <= n; j++) {
			scanf("%d", &a[i][j]);
			if(a[i][j] == 0) a[i][j] = -1; 
		} 
	for(int i = 1; i <= n; i++) {
		bool flg = 1;
		for(int j = 1; j <= n; j++) {
			if(a[i][j] == -1) {
				flg = 0;
				break;	
			} else {
				if(num[i][a[i][j]] == 0) kind[i]++;
				num[i][a[i][j]]++;
			}
		}
		can[i] = flg; 
	}
	for(int j = 1; j <= n; j++) {
		bool flg = 1;
		for(int i = 1; i <= n; i++) {
			if(a[i][j] == -1) {
				flg = 0;
				break;
			} else {
				if(num[n + j][a[i][j]] == 0) kind[n + j]++;
				num[n + j][a[i][j]]++;
			}
		}
		can[n + j] = flg;
	}
	for(int i = 1; i <= 2 * n; i++) {
		for(int j = 1; j <= 2 * n; j++) {
			if(can[j] == 1 && kind[j] == 1) {
				work(j);
				can[j] = 0;
				break;
			}
		}
	}
	reverse(ans + 1, ans + 1 + tot);
	printf("%d\n", tot);
	for(int i = 1; i <= tot; i++) {
		printf("%d %d\n", ans[i].first, ans[i].second);
	}
	return 0;
}

新-滑动窗口简单差分

典中典，\(\sum li \le10^{6}\)对于滑块顶到最左边与滑块顶到最右边相交的直接暴力做，如果不交，直接差分最大值，细节较多

#include<bits/stdc++.h>
using namespace std;
#define LL long long 
const int MAX = 1e6 + 70;
int n, w, l[MAX];
LL ans[MAX], cha[MAX];
LL a[MAX],b[MAX]; //统计
deque<LL> q;
void work(int h) {
	LL maxx = 0;
	vector<LL> Now; 
	Now.clear();
	Now.push_back(0); 
	for(int j = 1; j <= l[h]; j++) {
		LL x; scanf("%lld", &x);
		b[j] = x;
		maxx = max(maxx, x);
		Now.push_back(x);
	} 
	if(l[h] < w - l[h] + 1) { //不交 
		LL Max = 0;
		for(int i = 1; i <= l[h]; i++) {
			Max = max(Max, Now[i]);
			ans[i] += Max;
		}
		Max = 0;
		for(int i = w; i >= w - l[h] + 1; i--) {
			Max = max(Max, Now[l[h] - (w - i)]);
			ans[i] += Max; 		
		}
		cha[l[h] + 1] += maxx;
		cha[w - l[h] + 1] -= maxx;
	} else { //香蕉 
		memset(a, 0xcf, sizeof(a));
		while(!q.empty()) q.pop_back();
		int len = w - l[h] + 1;
		for(int i = 1; i <= l[h]; i++) {
			while(!q.empty() && i - q.front() + 1 > len) q.pop_front();
			while(!q.empty() && Now[q.back()] < Now[i]) q.pop_back();
			q.push_back(i);
			a[i] = max(a[i], Now[q.front()]);
		}
		for(int i = 1; i <= w - l[h]; i++) a[i] = max(a[i], 1LL * 0);
		while(!q.empty()) q.pop_back();
		Now.clear(); 
		for(int i = 0; i <= w - l[h]; i++) Now.push_back(0);
		for(int i = w - l[h] + 1; i <= w; i++) Now.push_back(b[i - (w - l[h])]);
		for(int i = w; i >= w - l[h] + 1; i--) {
			while(!q.empty() && q.front() - i + 1 > len) q.pop_front();
			while(!q.empty() && Now[q.back()] < Now[i]) q.pop_back();
			q.push_back(i);
			a[i] = max(a[i], Now[q.front()]);
		}	
		for(int i = l[h] + 1; i <= w; i++) {
			a[i] = max(a[i], 1LL * 0);
		} 
		for(int i = 1; i <= w; i++) {
			ans[i] += a[i];
		}
	}
}
int main() {
	freopen("windows.in","r",stdin);
	scanf("%d%d", &n, &w);
	for(int i = 1; i <= n; i++) {
		scanf("%d", &l[i]);
		work(i);
	}
	for(int i = 1; i <= w; i++) {
		cha[i] += cha[i - 1];
		printf("%lld ", ans[i] + cha[i]);
	}
	return 0;
}
/*
1 5
2 -10 10
*/

小明去旅游 锅

目前还不会，先锅着

Heavy and Frail：分治优化重复操作

35pts，二进制分组背包暴力跑

80pts 背包合并

发现只有单点修改，其他不变，跑一个前缀背包，跑一个后缀背包，对于查询，将前后两个背包合并，再插入**

//根据m非常小的性质， 且是单点修改， 完全可以维护前i个数的背包，与后i个数的背包， 查询时暴力合并，复杂度 m*m*q  * logc 
#include<bits/stdc++.h>
using namespace std;
#define LL long long 
const int MAX = 5100;
int n, m, q;
LL val[MAX], v[MAX], num[MAX];
LL f_pre[MAX][810], f_back[MAX][810]; //表示前i个数的背包， 后i个数的背包 
LL f[810], ans[MAX * 10];
struct made {
	int id; 
	LL x, y, z;
	int whr;
}ask[MAX * 10];
bool mycmp(made X, made Y) {
	return X.id < Y.id;
}
int main() {
	freopen("reflect.in","r",stdin);
	scanf("%d%d", &n, &m);
	for(int i = 1; i <= n; i++) scanf("%lld",&val[i]);
	for(int i = 1; i <= n; i++) scanf("%lld", &v[i]);
	for(int i = 1; i <= n; i++) scanf("%lld", &num[i]); 
	scanf("%d", &q);
	for(int i = 1; i <= q; i++) {
		scanf("%d%lld%lld%lld", &ask[i].id, &ask[i].x, &ask[i].y, &ask[i].z);
		ask[i].whr = i;
	}  
	sort(ask + 1, ask + 1 + q, mycmp);
	for(int i = 1; i <= n; i++) {
		for(int j = 1; j <= m; j++) f_pre[i][j] = f_pre[i - 1][j];
		int Num = num[i], k = 1;
		while(k <= Num) {
			LL V = k * v[i]; LL VAL = k * val[i]; 
			for(int j = m; j >= V; j--) f_pre[i][j] = max(f_pre[i][j], f_pre[i][j - V] + VAL);
			Num -= k;
			k *= 2;
		}
		if(Num != 0) {
			LL V = Num * v[i]; LL VAL = Num * val[i];
			for(int j = m; j >= V; j--) f_pre[i][j] = max(f_pre[i][j], f_pre[i][j - V] + VAL);
		}
	}
	for(int i = n; i >= 1; i--) {
		for(int j = 1; j <= m; j++) f_back[i][j] = f_back[i + 1][j];
		int Num = num[i], k = 1;
		while(k <= Num) {
			LL V = k * v[i]; LL VAL = k * val[i]; 
			for(int j = m; j >= V; j--) f_back[i][j] = max(f_back[i][j], f_back[i][j - V] + VAL);
			Num -= k;
			k *= 2;
		}
		if(Num != 0) {
			LL V = Num * v[i]; LL VAL = Num * val[i];
			for(int j = m; j >= V; j--) f_back[i][j] = max(f_back[i][j], f_back[i][j - V] + VAL);
		}
	}	
	for(int i = 1; i <= q; i++) {
		for(int j = 1; j <= m; j++) f[j] = 0;
		for(int j = 1; j <= m; j++) {
			for(int k = 0; k <= j; k++) {
				f[j] = max(f[j], f_pre[ask[i].id - 1][j - k] + f_back[ask[i].id + 1][k]);
			}
		}
		int Num = ask[i].z, k = 1;
		while(Num >= k) {
			LL V = ask[i].y * k; LL VAL = ask[i].x * k;
			for(int j = m; j >= V; j--) f[j] = max(f[j], f[j - V] + VAL);
			Num -= k;
			k *= 2;
		}
		if(Num) {
			LL V = ask[i].y * Num; LL VAL = ask[i].x * Num;
			for(int j = m; j >= V; j--) f[j] = max(f[j], f[j - V] + VAL);
		}
		ans[ask[i].whr] = f[m];
	}
	for(int i = 1; i <= q; i++) printf("%lld\n", ans[i]);
	return 0;
}

100pts

只有单点修改，前后缀的合并\(m^2\)没有拓展性，思考如果分治去做，\((l, r)\)代表到\((l,r)\)区间内除了\((l,r)\)都已经被加入背包，到\((x, x)\)时便统计答案，时间复杂度\(O(n*m*log_n^2+mq)\)
重复计算，分治

#include<bits/stdc++.h>
using namespace std;
#define LL long long 
const int MAX = 5010;
int n, m, q;
LL val[MAX], v[MAX], num[MAX], ans[MAX * 10];
LL f[900];
struct made { 
	int id;
	LL num, v, val; 
};
vector<made> ask[MAX];
void Nowwork(int l, int r) {
	for(int j = l; j <= r; j++) {
		int Num = num[j], k = 1;
		while(k <= Num) {
			LL V = k * v[j], VAL = val[j] * k;
			for(int j = m; j >= V; j--) f[j] = max(f[j], f[j - V] + VAL);
			Num -= k;
			k *= 2;
		}
		if(Num) {
			LL V = Num * v[j], VAL = val[j] * Num;
			for(int j = m; j >= V; j--) f[j] = max(f[j], f[j - V] + VAL);
		}
	}
}
void work(int x) {
	LL fnow[802];
	for(auto y : ask[x]) {
		int Num = y.num, k = 1;
		for(int i = 0; i <= m; i++) fnow[i] = f[i]; 
		while(k <= Num) {
			LL V = k * y.v, VAL = k * y.val;
			for(int i = m; i >= V; i--) f[i] = max(f[i - V] + VAL, f[i]);
			Num -= k;
			k *= 2;
		}
		if(Num) {
			LL V = Num * y.v, VAL = Num * y.val;
			for(int i = m; i >= V; i--) f[i] = max(f[i - V] + VAL, f[i]);
		}
		ans[y.id] = f[m];
		for(int i = 0; i <= m; i++) f[i] = fnow[i];
	}
}
void slove(int l, int r) {
	if(l == r) {
		work(l);
		return ;
	}
	int mid = (l + r) >> 1;
	LL fnow[810];
	for(int i = 0; i <= m; i++) fnow[i] = f[i];
	Nowwork(mid + 1, r);
	slove(l, mid);
	for(int i = 0; i <= m; i++) f[i] = fnow[i];
	Nowwork(l, mid);
	slove(mid + 1, r); 
}
int main() {
	freopen("reflect.in","r",stdin);
	scanf("%d%d", &n, &m);
	for(int i = 1; i <= n; i++) scanf("%lld", &val[i]);
	for(int i = 1; i <= n; i++) scanf("%lld", &v[i]);
	for(int i = 1; i <= n; i++) scanf("%lld", &num[i]);
	scanf("%d", &q);
	for(int i = 1; i <= q; i++) {
		int t; LL x, y, z; scanf("%d%lld%lld%lld", &t, &x, &y, &z);
		made Now; Now.id = i, Now.num = z, Now.v = y, Now.val = x;
		ask[t].push_back(Now);
	}
	slove(1, n);
	for(int i = 1; i <= q; i++) {
		printf("%lld\n", ans[i]);
	}
	return 0;
}

chess：根据题意分析

如果暴力DP，发现字符串比较在最劣情况下为\(O(n)\),显然过不了，考虑转化问题，如果在 第\(1\)步就不是最优的策略一定不会被用到第\(2\)步，所以基于这个性质，我们可以考虑每一步最优为什么，将可以跑到最优的存入set，只用set里面的元素更新下一步的最优，这样的时间复杂度就转化为了\(O((n + m)log)\)

#include<bits/stdc++.h>
using namespace std;
const int MAX = 2100;
#define PII pair<int, int>
char ch[MAX][MAX];
char minn[MAX + MAX];
queue<PII> q;
set<PII> s[MAX + MAX];
int n, m;
int main() {
	freopen("a.in","r",stdin);
	freopen("a.out","w",stdout);
	scanf("%d%d", &n, &m);
	for(int i = 1; i <= n; i++) 
		for(int j = 1; j <= m; j++) 
			cin>>ch[i][j];
	for(int i = 1; i <= n + m + 10; i++) minn[i] = 'z';
	minn[1] = ch[1][1];
	s[1].insert((PII){1, 1});
	for(int i = 2; i <= n + m; i++) {
		for(auto lst : s[i - 1]) {
			int x = lst.first, y = lst.second;
			if(x < n && minn[i] >= ch[x + 1][y]) {
				if(minn[i] > ch[x + 1][y]) s[i].clear();
				minn[i] = ch[x + 1][y];
				s[i].insert((PII){x + 1, y});
			} 
			if(y < m && minn[i] >= ch[x][y + 1]) {
				if(minn[i] > ch[x][y + 1]) s[i].clear();
				if(minn[i] > ch[x][y + 1]) minn[i] = ch[x][y + 1];
				s[i].insert((PII){x, y + 1});
			}
		}
	}
	for(int i = 1; i <= n + m - 1; i++) {
		cout<<minn[i];
	}
	return 0;
}

glass：简单装呀

数据范围，一眼状压，压什么? 我们发现一个瓶子只会被转移一次，且转移后一定不会再次转移，所以我们就压一个瓶子是否转移过即可，时间复杂度\(O(2^n*n*n)\)跑不满，所以能过

//一个瓶子只会被转移 
#include<bits/stdc++.h>
using namespace std;
#define LL long long 
const int MAX = (1 << 21);
int n, k, ANS = 1e9;
int f[MAX], c[25][25];
int Minn[MAX][21];
int main() {
	freopen("b.in","r",stdin);
	freopen("b.out","w",stdout);
	scanf("%d%d", &n, &k);
	for(int i = 0; i < n; i++) {
		for(int j = 0; j < n; j++) {
			cin>>c[i][j];	
		}
	} 
	memset(Minn, 0x3f, sizeof(Minn));
	for(int i = 0; i <= (1 << n) - 1; i++) {
		for(int j = 0; j < n; j++) {
			if(i >> j & 1) continue;
			for(int k = 0; k < n; k++) {
				if(k != j) if((i >> k & 1) == 0) Minn[i][j] = min(Minn[i][j], c[j][k]); 
			}
		}
	}
	memset(f, 0x3f, sizeof(f));
	f[0] = 0;
	for(int i = 0; i <= (1 << n) - 1; i++) {
		for(int j = 0; j < n; j++) {
			if((i >> j & 1) == 0) {
				f[i | (1 << j)] = min(f[i | (1 << j)], f[i] + Minn[i][j]);	
			} 
		}
	}
	int ans = 1e9;
	for(int i = 0; i <= (1 << n); i++) {
		int sum = 0;
		for(int j = 0; j < n; j++) {
			if((i >> j & 1) == 0) sum++;
		}
		if(sum == k) ans = min(ans, f[i]);
	}
	cout<<ans<<endl;
	return 0;
}

card：组合意义的DP

原题，但是之前没做，考场上也是一筹莫展
因为一个序列不同是操作顺序有一位不同即可，所以一定有组合意义，考虑如何将一个问题转化为一个组合问题

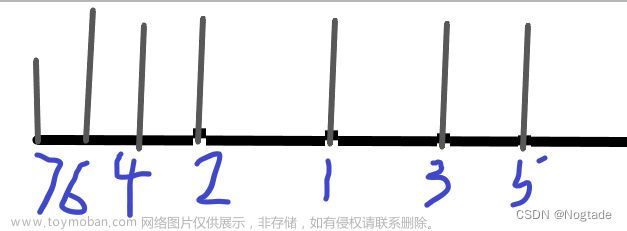
随意构造一个序列，我们发现根据题意操作

在\(1\)左侧的数下标一定递减，在\(1\)右侧的数下标递增
那么最大值是怎么统计的呢? 一定为左侧数的单调递增加上右侧数的单调递增的个数

但是要规定左侧的最大值，小于右侧单调递增的最小值

左侧单调递增在原序列中为以某个数(x)的单调递减序列

为了保证上述规定，右侧的单调递增的数也由x为起点，这样的话将总数减1即为最大严格递增子序列的长度
而总数如何计算，假设对于\(x\)而言由若干个组合可以构成最大严格递增子序列，对于其它的数除了1以外，往左放，往右放都无所谓，所以答案\(+=sum*(2^{n-len+1}/2)1\)

而求最长上升子序列，最长下降子序列需要一个\((log)\)做法，离散化后值域线段树即可

//一个序列不同，当且仅当操作序列不同， 具有计数优势
//在1左边的下标递减， 值递增， 在1右边的下标递增， 值递增
//考虑用一个数划分阶段
#include<bits/stdc++.h>
using namespace std;
#define LL long long 
//#define int long long
const int MOD = 1e9 + 7;
const int MAX = 2e5 + 70;
int n, a[MAX], b[MAX], tot; 
LL num_up[MAX], num_down[MAX];
LL f_up[MAX], f_down[MAX];
int lsh[MAX];
struct node { int f, num; };
struct SegmentTree {
	int l, r;
	LL f, num;
	#define l(x) tree[x].l
	#define r(x) tree[x].r
	#define f(x) tree[x].f
	#define num(x) tree[x].num
}tree[MAX * 4];
LL quick_mi(int x, int y) {
	LL xx = x, res = 1;
	while(y) {
		if(y & 1) res = res * xx % MOD;
		xx = xx * xx  % MOD;
		y = y / 2; 
	}
	return res;
}
void update(int p) {
	if(f(2 * p) > f(2 * p + 1)) { f(p) = f(2 * p); num(p) = num(2 * p) % MOD; }
	else if(f(2 * p + 1) > f(2 * p)) { f(p) = f(2 * p + 1); num(p) = num(2 * p + 1) % MOD; }
	else if(f(2 * p + 1) == f(2 * p)) { f(p) = f(2 * p); num(p) = (num(2 * p) + num(2 * p + 1)) % MOD; }
	return ;
}
void build(int p, int l, int r) {
	l(p) = l, r(p) = r, f(p) = num(p) = 0;
	if(l == r) { return ; }
	int mid = (l + r) >> 1;
	build(2 * p, l, mid);
	build(2 * p + 1, mid + 1, r);
}

node New(node x, node y) {
	if(x.f > y.f) return x;
	else if(y.f > x.f) return y;
	node NOW; NOW.f = x.f; NOW.num = (x.num + y.num) % MOD;
	return NOW;
}

node Find(int p, int l, int r) {
	if(l(p) >= l && r(p) <= r) {
		node NOW; NOW.f = f(p); NOW.num = num(p);
		return NOW;
	}	
	
	node NOW; NOW.f = 0, NOW.num = 0;
	int mid = (l(p) + r(p)) >> 1;
	if(l <= mid) NOW = New(NOW, Find(2 * p, l, r));
	if(r > mid) NOW = New(NOW, Find(2 * p + 1, l, r));
	return NOW;
}

void change(int p, int l, int r, int ff, int num) {
	if(l(p) == r(p)) {
		if(ff > f(p)) {
			f(p) = ff;
			num(p) = num % MOD;
		} else if(ff == f(p)) {
			num(p) = (num(p) + num) % MOD;
		}
		return ;
	}
	int mid = (l(p) + r(p)) >> 1;
	if(mid >= l) change(2 * p, l, r, ff, num);
	if(r > mid) change(2 * p + 1, l, r, ff, num);
	update(p); 
}

void Clear() { for(int i = 0; i <= 8e5 + 1; i++) tree[i].f = tree[i].num = 0; }

signed main() {
	freopen("c.in","r",stdin);
	scanf("%d", &n);
	for(int i = 1; i <= n; i++) {
		scanf("%d", &a[i]); b[i] = a[i];
	} 
	sort(b + 1, b + 1 + n);
	for(int i = 1; i <= n; i++) if(b[i] != b[i - 1]) lsh[++tot] = b[i];
	for(int i = 1; i <= n; i++) a[i] = lower_bound(lsh + 1, lsh + 1 + tot, a[i]) - lsh;
	reverse(a + 1, a + 1 + n);
	
	build(1, 0, 2e5 + 1);
	
	change(1, 2e5 + 1, 2e5 + 1, 0, 1);
	
	for(int i = 1; i <= n; i++) {
		node NOW = Find(1, a[i] + 1, 2e5 + 1);
		f_up[i] = NOW.f + 1;
		num_up[i] = NOW.num % MOD;
		change(1, a[i], a[i], f_up[i], num_up[i]);
	}
	
	Clear();
	
	change(1, 0, 0, 0, 1);
	for(int i = 1; i <= n; i++) {
		node NOW = Find(1, 0, a[i] - 1);
		f_down[i] = NOW.f + 1;
		num_down[i] = NOW.num % MOD;
		change(1, a[i], a[i], f_down[i], num_down[i]);
	}
	LL maxx = 0, NUM = 0;
	
	
	for(int i = 1; i <= n; i++) {
		if(f_up[i] + f_down[i] - 1 > maxx) { maxx = f_up[i] + f_down[i] - 1; NUM = 0; }
		if(f_up[i] + f_down[i] - 1 == maxx) NUM = (NUM + (1LL * num_up[i] * num_down[i] % MOD * quick_mi(2, n - f_up[i] - f_down[i] + 1) % MOD) ) % MOD;
	}
	cout<<maxx<<' '<<NUM<<endl;
	return 0;
}

godnumber:锅

ACAM套数位DP，还没打

meirin：暴力化简式子

简单数学题?
首先不考虑增加操作，如果单求
\(\sum_{l=1}^{n} \sum_{r=l}^{n}(\sum_{j=l}^{r}a_i)(\sum_{j=l}^{r}b_i)\)

考虑将里面的式子用前缀和表示出来即

\(\sum_{l=1}^{n} \sum_{r=l}^{n}(Sa_r-Sa_{l-1})(Sb_r-Sb_{l-1})\)

展开
\(\sum_{l=1}^{n} \sum_{r=l}^{n}(Sa_r*Sb_r+Sa_{l-1}*Sb_{l-1}-Sa_r*Sb_{l-1}-Sb{r}*Sa_{l-1})\)
令\(S_{ab_i}\)表示\(Sa_i*Sb_i\),\(SSa\)表示\(Sa\)的前缀和，\(SSb\)表示\(Sb\)的前缀和

将式子中的\(r\)累加起来 化简为\(\sum_{i=1}^{n}S_{ab_i}*n-Sa_{i-1}*(SSb_{n}-SSb_{i-1})-Sb_{i-1}*(SSa_{n}-SSa_{i-1})\)
这样就得到了一个\(NQ\) 时间复杂的的代码，考虑如果有修改，考虑修改的贡献
显然题目中只对\(b\)进行操作，考虑每个\(b\)对应的\(a\)区间和
\(\sum_{l=1}^{i}\sum_{r=i}^{n}\sum_{j=l}^{r}a_i\)
前缀优化一维
\(\sum_{l=i}^{i}\sum_{r=i}^{n}S_{a_r}-S_{a_{l-1}}\)
将式子拆开，分别积掉一个\(\sum\)后再相加

\(\sum_{i=1}^{n}i*(SS_{a_n}-SS_{a_{i-1}})-(n-i+1)(SS_{a_{i-1}})\)
再对这个式子求前缀和即可\(O1\)计算贡献,总时间复杂度\(O(n+q)\)

#include<bits/stdc++.h>
using namespace std;
#define LL long long 
#define lll 1LL 
const int MAX = 5e5 + 70;
const int MOD = 1e9 + 7;
int n, q;
int a[MAX], b[MAX], sa[MAX], ssa[MAX];
int g[MAX], sg[MAX];
LL ans;
int main() {
	scanf("%d%d", &n, &q);
	for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
	for(int i = 1; i <= n; i++) scanf("%d", &b[i]);
	for(int i = 1; i <= n; i++) sa[i] = (1LL * sa[i - 1] + 1LL * a[i] ) %MOD;
	for(int i = 1; i <= n; i++) ssa[i] = (1LL * ssa[i - 1] + 1LL * sa[i]) % MOD;
	for(int i = 1; i <= n; i++) {
		g[i] = ((1LL * i * ((1LL * ssa[n] - 1LL * ssa[i - 1] + MOD) % MOD) - (1LL * (n - i + 1) * (1LL * ssa[i - 1])) ) + MOD ) % MOD;	
	} 
	for(int i = 1; i <= n; i++) sg[i] = (1LL * sg[i - 1] + g[i] + MOD) % MOD;
	for(int i = 1; i <= n; i++) ans = (ans + (1LL * g[i] * b[i] % MOD) ) % MOD;
	for(int i = 1; i <= q; i++) {
		int l, r, k; scanf("%d%d%d", &l, &r, &k);
		ans = (ans + ((1LL * sg[r] - sg[l - 1] + MOD) % MOD * 1LL * k) % MOD + MOD) % MOD;
		printf("%lld\n", ans);
	}
	return 0;
}

sakuya:期望树形DP好题

最讨厌期望什么的了

首先不考虑修改

分析题意，要求期望难走程度，期望=概率*值

将值的贡献拆分成若干点对的贡献，发现每个点对在序列中相邻的概率是相同的

题意变为 \(\sum_{l=1}^{m}\sum_{r=1}^{m}dis(l,r)(l \ne r)*P\)

首先考虑\(P\)怎么计算， 发现\(P\)实际等于\(\frac{2*(m-1)A_{m-2}^{m-2}}{A_{m}^{m}}\)

接下来问题转化为点对之间的贡献如何计算,发现不好处理，考虑与上面相同的处理方式，将点对贡献转化为边权*出现次数

发现出现次数可以用\(f[v]*(m-f[v])\)计算得出(\(f[i]表示以i为根的子树中特殊点的个数\))
重新加回修改的限制

考虑对一个点的相连边增加\(k\)对答案的增量为什么?为相连边出现次数\(num\)×\(k\)

上述所有操作都可以在一次树形DP中处理，时间复杂度\(O(N+Q)\)

#include<bits/stdc++.h>
using namespace std;
#define int long long 
#define LL long long 
const int MAX = 5e5 + 70;
const int MOD = 998244353;
int tot, head[MAX], n, m, q, p[MAX], fa[MAX], f[MAX]; //表示以i为子树的特殊点的个数 
LL ans = 0;
int Num[MAX], sum[MAX];
vector<int> son[MAX];
vector<int> ce[MAX];
struct node { int u, v, val; }E[2 * MAX];
struct made { int l, t, id, val; }edge[MAX * 2];
void add(int u, int v, int id, int val) {
	edge[++tot].l = head[u];
	edge[tot].t = v;
	edge[tot].val = val;
	edge[tot].id = id;
	head[u] = tot;
}
void dfs_pre(int x, int Fa) {
	fa[x] = Fa;
	f[x] = p[x];
	for(int i = head[x]; i; i = edge[i].l) {
		int to = edge[i].t;
		if(to == Fa) continue;
		ce[x].push_back(to);
		son[x].push_back(to);
		dfs_pre(to, x);
		f[x] += f[to];
	}
}
LL quick_mi(int x, int y) {
	LL xx = x, res = 1;
	while(y) {
		if(y % 2) res = res * xx % MOD;
		xx = xx * xx % MOD;
		y /= 2;
	}
	return res % MOD;
}
signed main() {
	scanf("%lld%lld", &n, &m);
	for(int i = 1; i < n; i++) {
		int u, v, val; scanf("%lld%lld%lld", &u, &v, &val);
		E[i].u = u, E[i].v = v; E[i].val = val;
		add(u, v, i, val); add(v, u, i, val);
	}
	for(int i = 1; i <= m; i++) {
		int x; scanf("%lld", &x);
		p[x] = 1;
	}
	LL P_up = 1, P_down = 1, P;
	for(int i = 1; i <= m - 2; i++) P_up = (P_up * 1LL * i )% MOD;
	for(int i = 1; i <= m; i++) P_down = (P_down * 1LL * i) % MOD;
	P = 2LL * (m - 1) * P_up % MOD * quick_mi(P_down, MOD - 2) % MOD;
	dfs_pre(1, 0); //儿子节点， 父亲节点，相邻的边  
	for(int i = 1; i < n; i++) {
		if(E[i].u != fa[E[i].v]) swap(E[i].u, E[i].v);
		Num[E[i].v] = (f[E[i].v] * (m - f[E[i].v])) % MOD; 
	}
	for(int i = 1; i < n; i++) {
		if(E[i].u != fa[E[i].v]) swap(E[i].u, E[i].v);
		ans = (ans + (E[i].val * Num[E[i].v] % MOD) ) % MOD;		
	}
	for(int i = 1; i <= n; i++) {
		sum[i] = (sum[i] + Num[i]) % MOD;
		for(int j = 0; j < ce[i].size(); j++) sum[i] = (sum[i] + Num[ce[i][j]]) % MOD;
	}
	scanf("%lld", &q);
	for(int i = 1; i <= q; i++) {
		int x, k; scanf("%lld%lld", &x, &k);
		ans = (ans + (1LL * sum[x] * k)) % MOD;
		printf("%lld\n", (ans * P) % MOD);
	}
	return 0;
}

交换消消乐:简单性质题

将贡献拆成两部分，一部分为消除贡献显然为\(n\),另一部分为移动贡献

考虑对于一个元素\(i\),把\(i\)消掉需要多少步

设\(i\)左右端点分别为\(l_i,r_i\)

若只将\([l_i,r_i]\)中元素移除区间，不考虑移动左右端点

如果将\(i\)这个元素消掉，则需要\([l_i,r_i]\)中的出现次数为奇数的元素离开\([l_i,r_i]\)的区间

通过打表或手玩发现，移动次数为所有\([l_i,r_i]\)中出现奇数次的数的个数之和

这样我们就得到了一个\(n ^ 2\)做法，发现统计奇数次出现数目不好统计，正难则反

用\(r_i-l_i+1-2*num_{mod2=0}\)含义是区间长度减去出现偶数次的数的个数\(*2\)即为出现奇数次个数

发现满足\(l_i<=l_j\)和\(r_i>=r_j\)二维数点问题，树状数组维护即可

#include<bits/stdc++.h>
using namespace std;
#define LL long long 
const int MAX = 5e5 + 70;
int n,val[2 * MAX];
LL ans = 0, tree[MAX * 2];
bool bol[MAX];
struct made {
	int l, r;
}a[MAX];
bool mycmp(made X, made Y) { return X.l > Y.l; }
int lowbit(int x) { return x & (-x); }
LL Find(int x) {
	LL res = 0;
	for(int i = x; i; i -= lowbit(i)) res += tree[i];
	return res;
}
void add(int x) {
	for(int i = x; i <= 2 * n; i += lowbit(i)) tree[i] += 1;
}
int main() {
	scanf("%d", &n);
	for(int i = 1; i <= 2 * n; i++) {
		scanf("%d", &val[i]);
		if(bol[val[i]] == 0) {
			a[val[i]].l = i;
			bol[val[i]] = 1;
		} else a[val[i]].r = i;
	}
	sort(a + 1, a + 1 + n, mycmp);
	for(int i = 1; i <= n; i++) {
		LL res = Find(a[i].r);
		ans = ans + (a[i].r - a[i].l - 1 - 2 * res);
		add(a[i].r);
	}
	ans = ans / 2;
	ans = ans + n;
	printf("%lld\n", ans);
	return 0;
}

[ABC232H] King's Tour：构造，锅

Road of the King：神奇DP

神奇\(DP\),希望得到一个\(n^3\)的做法

首先发现\(1\)能到达所有点, 所以若一个图为强联通分量，当且仅当所有点都能到达\(1\)

不妨设计\(DP\)状态为\(f[i][j][k]\)表示已经走了\(i\)步，且经过了\(j\)个点，能够到达\(1\)点的个数为\(k\)的方案数

我们想初始值如何赋,根据状态可得\(f[0][1][1] = 1\)

转移分三种情况

1.若下一步前往了一个新的节点，得到转移 : \(f[i + 1][j + 1][k] += f[i][j][k] *(n-j)\)
2.若下一步重新去往了无法到达\(1\)的节点, 得到转移 \(f[i + 1][j][k]=f[i][j][k]*(j-k)\)
3.若下一步去往了任意一个可以到达\(1\)的节点，则可以使所有不能到达\(1\)的节点全部变为可以到达, 得到转移\(f[i+1][j][j]=f[i][j][k]*k\)
综上即可解决问题

题目的分析其实非常巧妙，为何这样设计状态，为何这样转移一定是正确的

都可以从题目要求每次都从当前节点指向下一节点,起点为\(1\) 这两个限制条件，或者关键性质得出，所以要多注意题目的限制条件，设计与限制条件有关的\(DP\)状态去解决问题

醉醉疯疯渺渺空空换根dp

经典题，考虑如何计数
两点不在一条链上，发现如果能统计每个点子树距离它的\(\sum 2^{dis}\)，此题就可做了
两点在一条链上，发现需要统计\(v\)子树外的点距离它的\(\sum2^{dis}\)\((dep[v]<dep[u])\),考虑求全集，然后减去\(v\)子树中的\(dis\)之和即为子树外的，然后全集就是换根求即可

F - Robot Rotation 不能随机化的折半搜索

数据范围提醒我们一定是一个优化后的指数级算法，考虑如何搜索.
根据题目的要求
我们发现\(x\)轴上移动只与奇数位的数字有关
\(y\)轴上的移动只与偶数位的数值大小有关
考虑\(x\)轴与\(y\)轴分离开,折半搜索可过

E - Revenge of "The Salary of AtCoder Inc." 期望

期望DP,感觉这块太薄弱了
期望一般都是倒着做的
考虑设计状态\(f[i]\)表示从 第\(i\)天为起点，直到结束的期望收益
发现\(f[i]是由\sum f_j (j >i)\)，然后发现可以前缀和优化，然后就做完了 ？

A. 1031模拟赛-A进步科学 状压DP

貌似可以称作状压经典套路题

如果一次操作结束前不能使用其他的操作，我们发现一位状态\(f[S]\)表示状态为\(S\)的最小时间即可解决

目前唯一的难点在于在一次操作结束前可以使用其他操作，这也就表示了可能会有多种操作在同一时间同时进行

那么最直观的感受当然是\(f[S][T]\)表示当前状态为 \(S\)还有的操作序列为\(T\)的最小时间，但是我们发现时间仍然不对

首先我们发现总时间不会超过\(2n\)

那么上面竟然也说了时间很关键，考虑将操作序列抽象为一个关于时间的排列，若第\(i\)位为\(0\)即代表这一秒没有操作，若第\(i\)秒为\(j\),则代表对\(j\)进行操作

考虑将某一个时刻的操作抽象成一个二进制数，每次异或这个数即为影响，但这样的时间复杂度为\(20^{20}\)

我们接着考虑优化，如果我们只记录相同状态的最小值就可以删去很多无用信息

那么我们结合上面的，大胆设计状态\(f[t][S]\)表示在\(t\)秒状态为\(S\)是否合法，但是如果我们考虑向序列后面加数的话，无法保证结束时间，不妨往操作序列前面加数，这样就类似枚举了一个终止时间，然后就可以转移了

时间复杂度\(O(n2^n)\)

B. 1031模拟赛-B吉吉没急 差分约束

是一道转换很巧妙的题

首先考虑用\(-1\)和\(1\)增加限制

先考虑\(-1\),首先用若设计\(f[x]\)表示\(x\)最早什么时候可以学会

那么\(-1\)的点的\(f[x]\)都为正无穷

如果其他点和\(-1\)的点有连边的话，那么最早只能在\(L + 1\)的时间连边

那么如果我们发现\(f[0]\)比\(0\)大的话说明不合法

然后用\(1\)考虑增加限制,然后判断每一个\(1\)是否合法

C. 1031模拟赛-C老杰克哒 动态DP

首先我们写出转移式

\(a[i] = 0\)

\(\qquad\)\(f[i][1] = min(f[i - 1][0] + 1, f[i - 1][1] + 1);\)

\(\qquad f[i][0] = min(f[i - 1][0], f[i - 1][1] + 2);\)

\(a[i] = 1\)

\(\qquad f[i][1] = min(f[i - 1][0], f[i - 1][1]);\)

\(\qquad f[i][0] = min(f[i - 1][0] + 1, f[i - 1][1] + 2);\)

我们发现转移式是线性的且有修改，那么就是动态DP无疑了

动态DP构造矩阵时可以把行看成输入值，把列看成输出值

线段树+矩阵维护一下

排座位 - 题目 - Daimayuan Online Judge] DP

如果没有不能相邻的限制的话，那么按照大小从小到大排序，两两配对即可得到最小值

接下来我们加入限制

下方黑色字代表的时排完序后的编号，上方绿色和红色字体是排序前的编号，紫色数字是空的下标

首先我们发现，如果有一对数\((fis,sed)\)它们排完序后仍然互斥，我们考虑把它们俩拆开，

当然最优方案是和\(fis\)前一个换一换，或者\(sed\)和后一个换一换

那么我们自然的设计\(dp\)状态\(f[i][0/1/2]\)分别代表这一对数不换，前一个数换，后一个数换

那么转移如下

\(if(AT same organize(a[i],a[i-1]))\)

\(\qquad f[i][0] = 0x3f3f3f3f3f3f3f\)

\(\qquad f[i][1] = f[i-2][2]+abs(a[i]-a[i-2])\)

\(\qquad f[i][0] = 0x3f3f3f3f3f3f3f\)

\(\qquad f[i][2] = min(f[i - 2][2] + abs(a[i - 2].val - a[i + 1].val), min(f[i - 2][0], f[i - 2][1])+ abs(a[i - 1].val - a[i + 1].val));\)

\(else\)

\(\qquad f[i][0] = min(min(f[i - 2][0], f[i - 2][1]) + abs(a[i - 1].val a[i].val), f[i - 2][2] + abs(a[i - 2].val - a[i].val));\)

A. 方块游戏 - 题目 - 多校信息学训练题库

普及题场上切不掉，真是个菜狗啊

首先考虑套路，差分一下区间修改变为了单点修改

这时候我们发现题目的要求就变成了将差分序列变为一段连续\(>1\)的段和一段\(<0\)的段

维护一下就行了

B. 雪球 - 题目 - 多校信息学训练题库

细节题，想不出来真菜啊👎

首先我们发现一个雪球最多能收集到的雪就是\(r[i]-l[i]+1\),\(r[i].l[i]\)分别表示它左右两个雪球

但是实际能收集多少呢?

对与左边的雪，应该是它向左与\(l[i]\)向右的长度恰好相接的长度，

对于右边的雪也是同理

然后我们发现每个雪球的移动的距离相同，不妨维护前\(i\)个时刻向左最长距离，向右最长距离

然后二分一下就行了，但是要注意细节，

因为有可能没有相切的时刻，那我们只能找下一次恰好交的位置

这时候统计雪的量的时候，我们还要看一看下一次实际有效移动，是向哪个方向，统计的量不同

D. 不要FQ - 题目 - 多校信息学训练题库 动态DP

因为可以向上向下跑，所以按照列为阶段

首先应该能够想出基本的\(DP\)

\(f[1][i]=f[1][i-1]*a[1][i]+(f[0][i-1]*a[0][i]*a[1][i])\)

\(f[0][i]=f[0][i-1]*a[0][i]+(f[1][i-1]*a[0][i]*a[1][i])\)

如果对于\(T>0\)的情况，我们选择直接构造一个\(2*2\)的矩阵

但是对于\(T=0\)的情况呢

我们不妨枚举左端点

然后考虑前\(i\)个的 \(sum\)

得到转移

\(sum[i] = sum[i-1]+f[i-1][0]+f[i-1][1]\) (这里求的不包含第\(i\)位)

然后发现也是线性的，可以将矩阵变成\(3*3\)的就行了

23zr提高day9-美人鱼 - 题目 - Zhengrui Online Judge (zhengruioi.com)

看完题解直接就懂了，非常套路

将区间排序

首先，如果区间互不交的话

显然我们每次单点修改只会对一个区间有影响，这样的话二分一下就行了

考虑区间有交

会对一些区间有影响，我们画一些情况观察一下，如果没有区间被包含的情况下，修改的应该是一段连续的下标

但是如果区间有包含呢?

显然被包含的区间没有用，把它们删除就可以了

然后区间修改线段树维护即可

题目详情 - 塔【NOIP2023模拟赛T2】 - 33OJ (33dai.cn)

首先对于三角形的DP，我们按列考虑

因为一列只会放一个\(2\),所以设计状态\(f[i][j]\)在第\(i\)列的第\(j\)行放一个\(2\)将前\(i\)列全部清空的最小代价，

转移很简单

\(f[i][j] = min(Min+cost, cost+f[i+1][j+1]-cost_{i+1,j+1})\)

然后我们就得到了\(n^2\) 的转移，

然后我们思考，什么时候我们才会放\(2\)

已知全部放\(1\)的代价是\(3n\)

在第\(h\)行放一个\(2\)的代价是\(\frac{h*(h+1)}{2}+2\)

若\(\frac{h*(h+1)}{2} \le 3n\)

近似\(h \le \sqrt{6n-2}\)

所以我们的复杂度就降到了\(n\sqrt{n}\)的级别了

Problem - 1738E - Codeforces

比赛考了这道题，现在还不是很会

首先暴力的想法是直接记忆化，发现若\(0\)很多的情况下一定会\(T\),考虑枚举断点

若\(psum(l,r)=bsum(l,r)\)则\(psum(r)=bsum(l)\)因为有意义的前题是前面也文章来源地址https://www.toymoban.com/news/detail-745910.html

到了这里，关于模拟赛好题分享的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！