前置芝士(了解即可啦~):C++、BST 二叉搜索树、堆、二叉堆
Treap 的概念
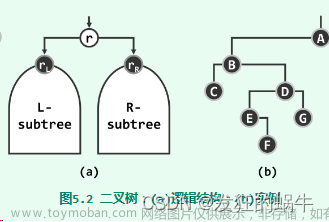
Treap 树堆,即树(Tree)+堆(Heap),是一棵弱平衡的二叉搜索树(BST),能同时满足二叉搜索树与堆的性质。
BST 满足任意一个节点的权值都大于等于左子树所有点的权值,且小于等于右子树所有点的权值的性质,我们可以用来求数的排名、前驱和后继,比如这是一棵可爱的 BST:

众所周知,当添加点的权值依次递增或递减时,一般 BST 将会退化成丑陋的链,such as:

那么每次添加点的时间复杂度便能被卡成 \(O(n)\),\(n\) 大一点就直接 TLE,寄。
为了规避一般 BST 容易退化成链的问题,Treap 光荣产生力!
Treap 在 BST 的基础上,为每个节点赋上了(随机的)优先值,并在建树时时刻维护堆的性质,由于随机性,建出来的树(也是一种二叉堆)深度期望大小为 \(log\ n\),因此规避了此类问题。
常规 Treap 的两种写法
常规 Treap 有两种写法,Splay 与 FHQ Treap:
Splay 为有旋 Treap,貌似是依靠左旋右旋节点的伸展操作来维护的 Treap,可以康康具体的图:

详细戳我
FHQ Treap 即无旋 Treap,与 Splay 不同,它只依靠分裂、合并能够进行添加节点、查询排名等等操作,分裂、合并如图:

FHQ Treap 相对来说代码量较小,也更好理解,应该更适合新手学习吧?
正题:FHQ Treap
FHQ Treap,其中 FHQ 指此做法的发明者——范浩强神犇,是依赖于分裂合并操作实现的 Treap,这种操作方式使得它天生支持维护序列、可持久化等特性,可持久化就以后再补吧。
基础节点信息、建点
首先我们需要一个 \(rt\) 表示树堆的根,\(l\)、\(r\) 表示左右儿子的 \(id\),还要存一个自己的权值 \(key\),当前子树大小 \(siz\),以及优先值 \(pri\),有必要的话还要存一个 \(lazy\) 标记。此外还需要一个更新节点信息的函数,当然,随机函数也可以自己手写 qwq,新建点就比较简单,代码如下:
#define uLL unsigned long long
......
int ...rt, gs...;
uLL sd=1;
uLL rd() {
return sd=sd*1145141ull*1145141ull;
}
struct node {
int l, r, siz, key, lazy;
uLL pri;
}tr[100005];
int blt(int key) {//新建点
++gs;
tr[gs].key=key;
tr[gs].lazy=0;
tr[gs].l=tr[gs].r=0; tr[gs].siz=1;
tr[gs].pri=rd();
return gs;
}
void upup(int now) {//更新节点信息
tr[now].siz=tr[tr[now].l].siz+tr[tr[now].r].siz+1;
}
基础的分裂、合并
上文有说到,FHQ Treap 即无旋 Treap,要依靠分裂、合并这两种基础操作。
按权值分裂
分裂有两种,第一种便是上图的按权值分裂,即给定 \(key\),分裂出所有点权值小于等于 \(key\) 的树堆 \(x\) 与所有点权值都大于 \(key\) 的树堆 \(y\),此分裂可以用于加点或求前驱、后继,带详解注释的代码如下:
void fl_key(int now, int key, int& x, int& y) {
if(!now) {//当前节点为空
x=y=0;
return ;
}
down(now);//有些题目需要用lazy标记下传,比如文艺平衡树中的区间反转操作
if(tr[now].key <= key) {
x=now;//权值小于等于key的添加到x树堆上,左子树一定在x树堆上
fl_key(tr[now].r, key, tr[now].r, y);
//再继续搜右子树,看右子树的点是添加到y树堆上(权值大于key)还是添到当前节点的右子树
}
else {
y=now;//权值大于key了就添加到y树堆上,而右子树一定也在y树堆上
fl_key(tr[now].l, key, x, tr[now].l);
//再继续搜左子树,看左子树的点是添加到x树堆上(权值小于等于key)还是添到当前节点的左子树
}
upup(now);//更新节点信息
}
盗来的模拟代码过程的 Gif 图:

上文说过,由于随机性,我们建出来的树堆的深度期望为 \(log\ n\) 层,而分裂相当于每层都只搜到了一次,所以分裂一次的时间复杂度是 \(O(log_2n)\)
按子树大小分裂
而第二种是按子树大小分裂,即给定 \(siz\),优先保留左子树,分裂出大小小于等于 \(siz\) 的树堆 \(x\),和剩余的树堆 \(y\)(可能没有),如图:

这种分裂可以用于一些特殊的操作(比如说文艺平衡树中的翻转区间),在普通平衡树中可用于求排名对应的值,带详解注释代码如下:
void fl_siz(int now, int siz, int& x, int& y) {
if(!now) {//空节点
x=y=0;
return ;
}
down(now);//有些题目需要用lazy标记下传,比如文艺平衡树中的区间反转操作
if(tr[tr[now].l].siz+1 <= siz) {
x=now;//左子树+自己的size小于等于siz,将左子树和自己加到树堆x上
fl_siz(tr[now].r, siz-tr[tr[now].l].siz-1, tr[now].r, y);
//接着搜右子树(注意!!!siz要减去左子树+当前节点的size!!!)
}
else {
y=now;//不行的话就连同右子树加到树堆y上,看左子树能不能加到树堆x上
fl_siz(tr[now].l, siz, x, tr[now].l);
}
upup(now);//更新节点信息
}
和按权值分裂的时间复杂度一样,\(O(log_2n)\)
合并
合并操作只有一种,但是要求合并的两个树堆 \(x\)、\(y\),树堆 \(x\) 的所有点的权值都要严格小于树堆 \(y\) 的任意点,(但本蒟蒻还有幸遇见过答辩题要用 fhq treap 合并有交集的树堆的),而此处就要用到我们赋予的优先值啦,如图(可能看起来有点难懂):

如图所示,合并时优先考虑优先值,并以优先的点为合并后的父节点,然后再将非优先点与优先点的儿子合并,这是一个递归的过程,要注意的是合并要从祖先开始,且一般合并是直接合并两个无交集的树,若是有交集那么这个合并就只能用添加点的做法(详见下文),此处直接上代码吧:
int merge(int x, int y) {//合并时需要已经满足x的所有点的权值小于y的所有点的权值
down(x);//有需要的话标记下传
down(y);
if(x == 0 || y == 0) return x+y;//x、y有一个为空节点直接返回非空的节点
if(tr[x].pri < tr[y].pri) {//维护堆的性质,用优先值确定父亲
tr[x].r=merge(tr[x].r, y);//y应该在x的右子树,因此要合并x的右儿子和y
upup(x);//更新节点信息
return x;//返回当前根节点
}
else {
tr[y].l=merge(x, tr[y].l);//x应该在y的左子树,因此要合并y的左儿子和x
upup(y);//更新节点信息
return y;//返回当前根节点
}
}
合并的话递归层数取决于树堆深度,而深度期望为 \(log\ n\) 层,那么一次合并操作时间复杂度便为 \(O(log_2n)\)
添加点
既然我们已经会分裂、合并了,那么如果想要添加一个值为 \(X\) 的点,我们可以直接将原树堆按 \(key = X\),以权值大小分裂,然后新建点,将分裂出的树堆 \(x\) 和新建点合并后再和分裂出的树堆 \(y\) 合并,时间复杂度为 \(O(log_2n)\),如图:

此处为什么不直接合并原树堆和新建点呢?那是因为我们写的 \(merge\) 合并函数要求合并的是无交集的两树堆,且树堆 \(x\) 的所有点的权值都要严格小于树堆 \(y\) 的任意点,所以我们必须要先分裂再合并以保证树堆的正确性,代码如下:
void insert(int key) {
int x, y;
fl_key(rt, key, x, y);
rt=merge(merge(x, blt(key)), y);
}
删除点
删除一个值为 \(X\) 的点的话可以先按 \(key = X\),以权值大小分裂得到树堆 \(x\)、\(y\),再按 \(key = X-1\),以权值大小分裂树堆 \(x\),得到树堆 \(z\)、\(a\),然后将树堆 \(a\) 的根节点丢掉(即合并 \(a\) 的左右儿子,不合并 \(a\) 的根节点,这就相当于删了一个点),所有树堆依次合并,时间复杂度依然为 \(O(log_2n)\),如图:

代码如下:
void dlt(int key) {
int x, y, z;
fl_key(rt, key, x, y);
fl_key(x, key-1, z, x);
rt=merge(merge(z, merge(tr[x].l, tr[x].r)), y);
}
查询排名
若是查询 \(X\) 的排名,直接按 \(key = X-1\),以权值大小分裂得到树堆 \(x\)、\(y\),答案为树堆 \(x\) 的 \(size+1\),时间复杂度为 \(O(log_2n)\),代码如下:(注意最后要合并回来!)
int ask(int key) {
int x, y, ret=0;
fl_key(rt, key-1, x, y);
ret=tr[x].siz+1;
rt=merge(x, y);
return ret;
}
查询排名对应的值
查询排名 \(X\) 对应的值,有两种做法。
其一是上文提及的按子树大小分裂,按 \(siz = X-1\),以子树大小分裂得到树堆 \(x\)、\(y\),然后再按 \(siz = 1\),以子树大小分裂树堆 \(y\),得到树堆 \(a\)、\(z\),\(a\) 的根节点的值就是答案,时间复杂度为 \(O(log_2n)\),代码如下:(注意最后都要合并回来!)
int asks(int siz) {
int x, y, z;
fl_siz(rt, siz-1, x, y);
fl_siz(y, 1, y, z);
int ret = tr[y].key;
rt = merge(merge(x, y), z);
return ret;
}
其二是直接硬上,从根节点开始 dfs,如果左儿子+自己的 \(size\) 比 \(X\) 小,那么 \(X\) 减去 \(size\),搜右儿子,否则就搜左儿子,\(X = 0\) 时就输出当前点的权值,时间复杂度依旧是 \(O(log_2n)\)(毕竟深度期望为 \(log\ n\)),代码如下:
int asks(int siz) {
int o = rt;
while(1) {
int qwq = tr[tr[o].l].siz+1;
if(qwq == siz) break;
if(siz < qwq) o=tr[o].l;
else o=tr[o].r, siz-=qwq;
}
return tr[o].key;
}
查询前驱、后继
查询 \(X\) 的前驱,先按 \(key = X-1\),以权值大小分裂得到树堆 \(x\)、\(y\),然后从树堆 \(x\) 的根节点开始,右儿子非空就一直往右边走(因为树堆 \(x\) 的所有点已经满足了其点值小于等于 \(X-1\),只需找到里面最大的点值),最后输出即可。
查询 \(X\) 的后继,先按 \(key = X\),以权值大小分裂得到树堆 \(x\)、\(y\),然后从树堆 \(y\) 的根节点开始,左儿子非空就一直往左边走(因为树堆 \(y\) 的所有点已经满足了其点值大于 \(X\),只需找到里面最小的点值),最后输出即可。
时间复杂度均为 \(O(log_2n)\),代码:(注意最后都要合并回来!)
int findl(int key) {
int x, y, ret=0;
fl_key(rt, key-1, x, y);
ret=x;
while(tr[ret].r != 0) ret=tr[ret].r;
ret=tr[ret].key;
rt=merge(x, y);
return ret;
}
int findr(int key) {
int x, y, ret=0;
fl_key(rt, key, x, y);
ret=y;
while(tr[ret].l != 0) ret=tr[ret].l;
ret=tr[ret].key;
rt=merge(x, y);
return ret;
}
普通平衡树——代码整合
总的时间复杂度大致为 \(O(n\times log_2n)\),\(n\) 表示操作数量。
#include <bits/stdc++.h>
#define uLL unsigned long long
using namespace std;
int n, opt, k, gs, rt;
uLL sd=1;
uLL rd() {
return sd=sd*1145141ull*1145141ull;
}
struct node {
int l, r, siz, key;
uLL pri;
}tr[100005];
int blt(int key) {
++gs;
tr[gs].key=key;
tr[gs].l=tr[gs].r=0; tr[gs].siz=1;
tr[gs].pri=rd();
return gs;
}
void upup(int now) {
tr[now].siz=tr[tr[now].l].siz+tr[tr[now].r].siz+1;
}
void fl_key(int now, int key, int& x, int& y) {
if(!now) {
x=y=0;
return ;
}
if(tr[now].key <= key) {
x=now;
fl_key(tr[now].r, key, tr[now].r, y);
}
else {
y=now;
fl_key(tr[now].l, key, x, tr[now].l);
}
upup(now);
}
int merge(int x, int y) {
if(x == 0 || y == 0) return x+y;
if(tr[x].pri < tr[y].pri) {
tr[x].r=merge(tr[x].r, y);
upup(x);
return x;
}
else {
tr[y].l=merge(x, tr[y].l);
upup(y);
return y;
}
}
void insert(int key) {
int x, y;
fl_key(rt, key, x, y);
rt=merge(merge(x, blt(key)), y);
}
void dlt(int key) {
int x, y, z;
fl_key(rt, key, x, y);
fl_key(x, key-1, z, x);
rt=merge(merge(z, merge(tr[x].l, tr[x].r)), y);
}
int ask(int key) {
int x, y, ret=0;
fl_key(rt, key-1, x, y);
ret=tr[x].siz+1;
rt=merge(x, y);
return ret;
}
int asks(int siz) {
int o = rt;
while(1) {
int qwq = tr[tr[o].l].siz+1;
if(qwq == siz) break;
if(siz < qwq) o=tr[o].l;
else o=tr[o].r, siz-=qwq;
}
return tr[o].key;
}
int findl(int key) {
int x, y, ret=0;
fl_key(rt, key-1, x, y);
ret=x;
while(tr[ret].r != 0) ret=tr[ret].r;
ret=tr[ret].key;
rt=merge(x, y);
return ret;
}
int findr(int key) {
int x, y, ret=0;
fl_key(rt, key, x, y);
ret=y;
while(tr[ret].l != 0) ret=tr[ret].l;
ret=tr[ret].key;
rt=merge(x, y);
return ret;
}
int main() {
scanf("%d", &n);
for(int i = 1; i <= n; ++i) {
scanf("%d%d", &opt, &k);
if(opt == 1) insert(k);
else if(opt == 2) dlt(k);
else if(opt == 3)
printf("%d\n", ask(k));
else if(opt == 4)
printf("%d\n", asks(k));
else if(opt == 5)
printf("%d\n", findl(k));
else if(opt == 6)
printf("%d\n", findr(k));
}
return 0;
}
文艺平衡树
建议做完普通平衡树后就直接上这道题,也许能让你对平衡树的理解加深哦 qwq
题目简述
初始有长度为 \(n\) 的 \(1\)、\(2\)、\(3\)……\(n-1\)、\(n\) 的原序列,进行 \(m\) 次翻转 \([l, r]\) 区间的数后,输出当前序列。
题解
既然题目有个平衡树,那我们直接 FHQ Treap 硬上吧!Wait Wait Wait,仔细想想,题目要求我们维护一个序列,那我们一定也要用 FHQ Treap 维护这个序列,但是他需要支持区间翻转操作,那么我们就需要将问题转化一下了 qaq。
对于每一次操作 \([l, r]\),我们先假设我们能用 FHQ Treap 分裂得到 \([l, r]\) 对应的树堆,接下来我们的问题便是区间翻转了。
假设有一个树:

因为 Treap 是一棵二叉树,而原序列建出来的 Treap 能按中序遍历输出得到原序列,我们可以考虑最后用中序遍历输出答案。若是将图中的树中序遍历,输出为 \(c-a-d-u-b\),而整个区间翻转就相当于把中序遍历给翻转了,即 \(b-u-d-a-c\),我们再将新中序遍历结果对应的树画出来:

可以发现,翻转中序遍历结果相当于将树上每个点的左右儿子互换……
OMG,思路不就这么出来了,先用 FHQ Treap 分裂得到 \([l, r]\) 对应的树堆,然后翻转每个点的左右儿子,最后再合并回去,这样就 OK 啦!因为直接做翻转每个点的左右儿子会 TLE 穿,所以我们可以存一个 \(lazy\) 标记,多次翻转的话就每次给标记异或上一个 \(1\),在分裂、合并时下传标记即可,能够保证不会将标记传到假儿子上,时间复杂度为 \(O(m\times log_2n)\)
那么我们现在就只需要找到一种分裂方法能够把 \([l, r]\) 区间对应的树堆分裂出来就行了,因为有交换左右儿子的操作,那么原 Treap 就不满足二叉搜索树的性质了,我们也因此不能按权值大小分裂,否则就算使其满足了性质,也会将标记下传到假儿子上去。
此时,“按子树大小分裂”的分裂方法就能起到很大的作用了!
有一个显然的性质:对于序列的一个区间内的所有数,在该区间对应的树堆中所对应的节点也是两两相连的。这个性质就能够保证我们按子树大小分裂的正确性啦,我们可以先按 \(siz = l-1\) 分裂得到树堆 \(x\)、\(y\),然后我们再按 \(siz = r-l+1\) 分裂树堆 \(y\) 得到树堆 \(a\)、\(z\),并给树堆 \(a\) 打上标记,最后再合并回去,而在分裂、合并时我们再进行标记下传即可。
最后我们按中序遍历输出就是答案惹!
总时间复杂度为 \(O(n \times log_2n)\) 左右,可以接受,代码如下:文章来源:https://www.toymoban.com/news/detail-746023.html
#include <bits/stdc++.h>
#define uLL unsigned long long
using namespace std;
int n, m, l, r, gs, rt;
uLL sd=1;
uLL rd() {
return sd=sd*1145141ull*1145141ull;
}
struct node {
int l, r, siz, key, lazy;
uLL pri;
}tr[100005];
int blt(int key) {
++gs;
tr[gs].key=key;
tr[gs].lazy=0;
tr[gs].l=tr[gs].r=0; tr[gs].siz=1;
tr[gs].pri=rd();
return gs;
}
void upup(int now) {
tr[now].siz=tr[tr[now].l].siz+tr[tr[now].r].siz+1;
}
void fl_key(int now, int key, int& x, int& y) {
if(!now) {
x=y=0;
return ;
}
if(tr[now].key <= key) {
x=now;
fl_key(tr[now].r, key, tr[now].r, y);
}
else {
y=now;
fl_key(tr[now].l, key, x, tr[now].l);
}
upup(now);
}
void down(int now) {//lazy标记下传
if(now == 0 || tr[now].lazy == 0) return ;
swap(tr[now].l, tr[now].r);
tr[tr[now].l].lazy^=1;
tr[tr[now].r].lazy^=1;
tr[now].lazy=0;
}
void fl_siz(int now, int siz, int& x, int& y) {//按siz分裂
if(!now) {
x=y=0;
return ;
}
down(now);
if(tr[tr[now].l].siz+1 <= siz) {
x=now;
fl_siz(tr[now].r, siz-tr[tr[now].l].siz-1, tr[now].r, y);
}
else {
y=now;
fl_siz(tr[now].l, siz, x, tr[now].l);
}
upup(now);
}
int merge(int x, int y) {//此时的merge已经不要求x的所有点的权值小于y的所有点的权值了,因为有交换操作,这个Treap已经无法满足二叉搜索树的性质,但是本题也不用这个性质
down(x);
down(y);
if(x == 0 || y == 0) return x+y;
if(tr[x].pri < tr[y].pri) {//相当于只是建了个堆
tr[x].r=merge(tr[x].r, y);
upup(x);
return x;
}
else {
tr[y].l=merge(x, tr[y].l);
upup(y);
return y;
}
}
void insert(int key) {//新加点,此时的Treap满足二叉搜索树的性质
int x, y;
fl_key(rt, key, x, y);
rt=merge(merge(x, blt(key)), y);
}
void change() {//进行区间翻转操作
int x, y, z;
fl_siz(rt, l-1, x, y);
fl_siz(y, r-l+1, z, y);
tr[z].lazy^=1;//打上标记
rt=merge(merge(x, z), y);//从左往右merge,保持原siz顺序
}
void dfs(int now) {//中序遍历输出
down(now);
if(tr[now].l != 0)
dfs(tr[now].l);
printf("%d ", tr[now].key);
if(tr[now].r != 0)
dfs(tr[now].r);
}
int main() {
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; ++i)
insert(i);
for(int i = 1; i <= m; ++i) {
scanf("%d%d", &l, &r);
change();
}
dfs(rt);putchar('\n');
return 0;
}
完结撒花~可持久化以后再来补吧文章来源地址https://www.toymoban.com/news/detail-746023.html
到了这里,关于FHQ Treap学习笔记的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!