二分（折半查找）详细解答（边界条件终止条件等等详细解释）-Toy模板网

这篇具有很好参考价值的文章主要介绍了二分（折半查找）详细解答（边界条件终止条件等等详细解释）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

刷 Leetcode 总能遇到关于二分的题目，但是之前也只是草草地了解一下，每次在使用的时候都需要找模板，要不然就需要对于边界条件进行调试，着实是很麻烦！！！

二分介绍：

首先来简单介绍一下二分：二分查找也称折半查找（Binary Search），它是一种效率较高的查找方法。但是，折半查找要求 线性表 必须采用 顺序存储结构，而且表中元素按关键字有序排列。

优点：

比较次数少：二分查找每次将搜索范围缩小一半，因此比较次数较少，查找速度快。
时间复杂度低：在有序数组中，二分查找的时间复杂度为O(log n)，其中n为搜索范围的大小。相比线性查找的O(n)时间复杂度，二分查找更高效。
可靠性高：由于二分查找是基于有序数组进行的，因此在数组有序的前提下，可以保证查找结果的准确性。

缺点：

要求有序数组：二分查找要求待查表为有序表，如果数组无序，则需要先进行排序操作，增加了额外的时间复杂度。
插入删除困难：由于二分查找是基于有序数组进行的，插入和删除操作会破坏数组的有序性，因此在插入和删除元素时需要维护数组的有序性，增加了操作的复杂度。

适用范围以及题型：

　　在一段有序序列中寻找指定元素（或者该序列中不存在指定元素，返回小于等于指定元素的最大值）等等

二分法讲解：

arr数组为有序序列
left: 左边界  
right:右边界  
mid = (left + right) / 2: 中间下标
循环条件: left .. right

上述为二分中的左边界（left），右边界（right），中间元素下标（mid）.

二分法分类：

1.闭区间（左边界 left = 0, 右边界 right = arr.size() - 1）（从序列中能够找到对应的元素）

先插入代码：

        // 1 2 3 5 6 8 9 10（有序数组中的元素）
        int left = 0, right = arr.size() - 1;
        int goal = 5;
        while(left <= right){
            int mid = ( left + right) / 2;
            if(goal > arr[mid]){
                left = mid + 1;
            }else{
                right = mid - 1;
            } 
            cout << "Left:" << left << "  " << "Right:" << right << "     " ;
        }     
        cout << "结果是" << left << endl;

我们直接进行分析（先不要想为什么这样子，先跟着我的思路走）：
（1）闭区间初始化：
　　left = 0, right = arr.size() - 1，则此时 left 和 right 代表的分别是数组序列的起始元素和末尾元素
（2）循环条件的设置：
　　循环结束的标志是区间内没有元素，因此只有当 left < right 的时候才会终止，因此设置 while（left <= right）
（3）循环中 if 语句满足与不满足后的 left 和 right 的设置
　　暂时不讨论为什么这样子设置

来看终止情况：
终止前的一次： left == right
设 X = left, Y = right (这里的X和Y是不会变的，因为此时 left == right，所以可以 X == Y)
此时 mid == X (或者Y)，结果只有两种可能，goal对应元素下标为（1）X对应的或者（2）X + 1对应的
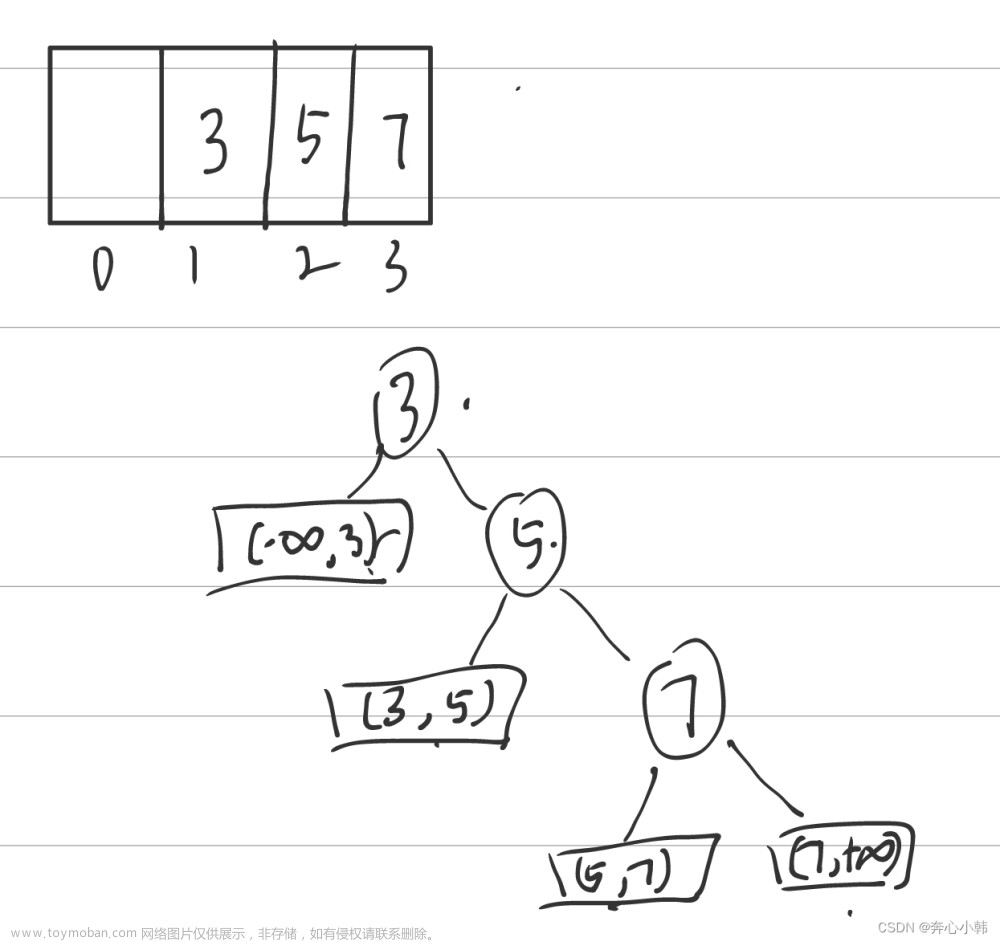
　　　　前面这句话不理解可以看 while 循环中的 if 语句，流程图如下：

接着我们分析两种情况:
情况一：X对应的元素是目标值
　　则此时进入 if 语句，判断为 N，进入第二个执行语句： right = mid - 1, 则此时 left 不变，结果就是 left，就是 X

情况二：X + 1对应的元素是目标值
　　则此时进入 if 语句，判断为 Y，进入第一个执行语句：left = mid + 1，则此时结果仍然是 left, 就是Ｘ + 1

综上：cout << left << endl; 就可以得到正确答案！

2.闭区间从序列中寻找小于等于目标值的最大元素

先插入代码：

       // 1 2 3 5 6 8 9 10（有序数组中的元素） 
       bool flag = true;
       int left = 0, right = arr.size() - 1, goal = 11;
       while(left <= right){
           int mid = ( left + right) / 2;
           if(goal > arr[mid]){
               left = mid + 1;
           }else if(goal == arr[mid]){
               cout << "找到相等的元素： "<< mid << endl;
               flag = false;
               break;
           }else{
               right = mid - 1;
           }
        }     
        if(flag) cout << " 小于goal的最大元素下标是" << right << endl;

分析：首先若是区间中出现了与 goal 值相等的元素，则直接返回；
这个是没有问题的，我们考虑如下情况：其中不存在等于 goal 的元素，则进行以下分析：

来看终止情况：
终止前的一次： left == right
设 X = left, Y = right (这里的X和Y是不会变的，因为此时 left == right，所以可以 X == Y)
此时 mid == X (或者Y，因为X == Y)，结果只有两种可能，goal对应元素下标为 :（1）X对应的或者（2）X - 1对应的
接着我们分析两种情况:（注意：以下情况考虑的时候没有考虑 goal == arr[mid]，因为若是出现这种情况则直接结束循环）

情况一：X对应的元素是目标值
　　则此时进入 if 语句，判断为 Y，进入第一个执行语句： left = mid + 1, 则此时 right 不变，结果就是 right，就是 Y (X == Y)

情况二：X - 1对应的元素是目标值
　　则此时进入 if 语句，判断为 N，进入第一个执行语句：right = mid - 1，则此时结果是 right, 就是 Y - 1 (Y - 1 == X - 1)

综上：cout << right << endl; 就可以得到正确答案！

文章来源地址https://www.toymoban.com/news/detail-746038.html

到了这里，关于二分（折半查找）详细解答（边界条件终止条件等等详细解释）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！