前缀和差分-Toy模板网

这篇具有很好参考价值的文章主要介绍了前缀和差分。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

前缀和

前缀和定义

对于数列A，它的前缀和数列S[i]就表示数列A从第一个元素到第i个元素的总和。

计算公式

// 前缀和数列S   原数列A
S[i] = S[i - 1] + A[i];
//S[i - 1] 表示i-1个元素的和加上A[i],就构成了前i个元素的和S[i]

具体应用

前缀和的主要用处：求任意区间的区间和

一般通过遍历求和的时间复杂度是O(n),通过前缀和可以减少为O(1)

具体解法如下:

前缀和计算区间[l,r]的区间和：S[r] - S[l - 1]

模板

ACWing 795前缀和

#include <iostream>
const int N = 100010;
int a[N],b[N];
int main(void){
    int n,m;
    scanf("%d %d",&n,&m);
    for (int i = 1;i <= n;i++) scanf("%d",&a[i]);
    for (int i = 1;i <= n;i++) b[i] = b[i - 1] + a[i];
    while (m --) {
        int l,r;
        scanf("%d %d",&l,&r);
        printf("%d\n",b[r] - b[l - 1]);
    }
    return 0;
}

Tips:

让元素下标从1开始。也就是下标为0的元素赋值为0

这样的好处是可以计算前i个元素的和，减少特判的情况。

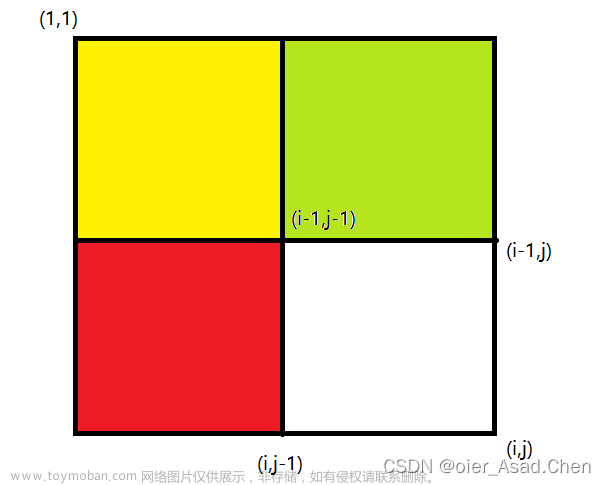
二维前缀和计算公式

//二维前缀和
S[i][j] = S[i - 1][j] + S[i][j - 1] - S[i - 1][j - 1] +A[i][j];
//二维前缀和的作用也是为了快速计算区块和
res = S[x2][y2] - S[x1 - 1][y2] - S[x2][y1 - 1] + S[x1 - 1][y1 - 1];

二维前缀和模板

ACWing 796 子矩阵的和

#include <iostream>
const int N = 1010;
int a[N][N],b[N][N];
int main(){
    int n,m,q;
    scanf("%d%d%d",&n,&m,&q);
    for (int i = 1;i <= n;i++){
        for (int j = 1;j <= m;j++){
            scanf("%d",a[i][j]);
            b[i][j] = b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1] + a[i][j];
        }
    }
    while (q --) {
        int x1,y1,x2,y2;
        scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
        printf("%d\n",b[x2][y2] - b[x1 - 1][y2] - b[x2][y1 - 1] + b[x1 - 1][y1 - 1]);
    }
    return 0;
        
}

差分（前缀和的逆运算)

定义

给定一个数列 A 那么它的差分数列 B中的B[i] 表示为 A 中第i个元素与第i - 1个元素的差。

B[i] = A[i] - A[i - 1] (1 <= i <= n);

具体应用

// 差分的主要应用 就是快速的给 A 的区间[l,r] 加上d
// 将A[l,r]加d ==> 将差分数列 B[l] 加 d 再将B[r + 1]减d

模板

ACWing 797.差分

#include <iostream>
const int N = 100010;
int a[N],b[N];
int main(void){
    int n,m;
    scanf("%d%d",&n,&m);
    for (int i = 1;i <= n;i++) scanf("%d",&a[i]);
    //构造差分数组
    for (int i = 1;i <= n;i++) b[i] = a[i] - a[i - 1];
    while (m --) {
        int l,r,c;
        scanf("%d%d%d",&l,&r,&c);
        b[l] += c;
        b[r + 1] -= c;
    }
    for (int i = 1;i <= n;i++) b[i] += b[i - 1];
    for (int i = 1;i <= n;i++) printf("%d ",b[i]);
    return 0;
}

二维差分公式

// 对A矩阵中该区块的每个元素加上d的操作 相当于对B进行四个操作
B[x1][y1] += d;
B[x2 + 1][y1] -= d;
B[x1][y2 + 1] -= d;
B[x2 + 1][y2 + 1] += d;

二维差分模板

ACWing 789.差分矩阵文章来源地址https://www.toymoban.com/news/detail-746156.html

#include <iostream>
const int N = 1010;
int a[N][N],b[N][N];
void insert (int x1,int y1,int x2,int y2,int d) {
    b[x1][y1] += d;
    b[x2 + 1][y1] -= d;
    b[x1][y2 + 1] -= d;
    b[x2 + 1][y2 + 1] += d;
}
int main(void){
    int n,m,q;
    scanf("%d%d%d",&n,&m,&q);
    for (int i = 1;i <= n;i++) {
        for (int j = 1;j <= m;j++) {
            scanf("%d",&a[i][j]);
            insert(i,j,i,j,a[i][j]);
        }
    }
    while (q --) {
        int x1,y1,x2,y2,d;
        scanf("%d%d%d%d%d",&x1,&y1,&x2,&y2,&d);
        insert(x1,y1,x2,y2,d);
    }
    for (int i = 1;i <= n;i ++) {
        for (int j = 1;j <= m;j++) {
            a[i][j] = a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1] + b[i][j];
        }
    }
    for (int i = 1;i <= n;i++) {
        for (int j = 1;j <= m;j++) {
            printf("%d ",a[i][j]);
        }
        printf("\n");
    }
    return 0;
    
}

到了这里，关于前缀和差分的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！