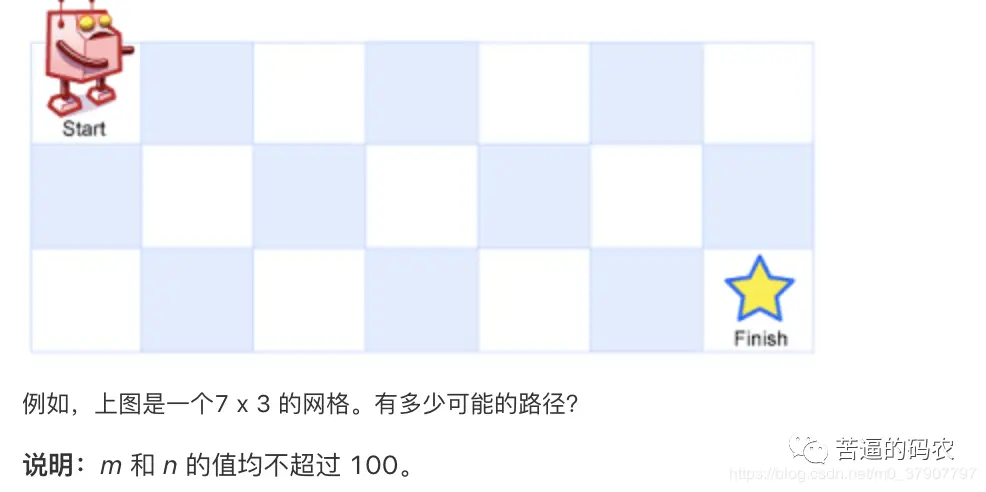
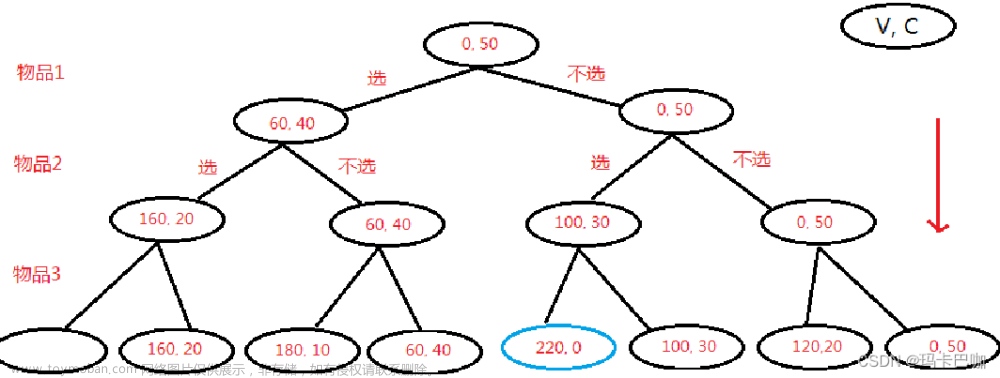
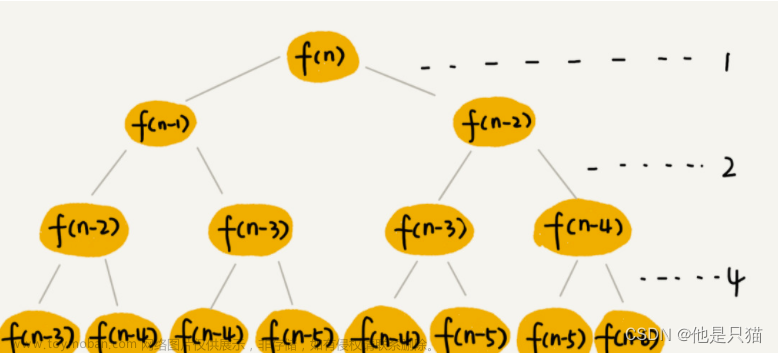
上一篇文末已经提到了记忆化搜索是动态规划(Dynamic Programming)的一种形式,是一种自顶向下(Top-Down)的思考方式,通常采用递归的编码形式;既然动态规划有自顶向下(Top-Down)的递归形式,自然想到对应的另外一种思考方式自底向上( Bottom-Up ),也就是本篇要写的内容。
什么是自底向上的思考?不空谈理论,还是借个实际题目来体会。
自底向上( Bottom-Up )
LeetCode 53. 最大子数组和【中等】
给你一个整数数组nums请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。子数组 是数组中的一个连续部分。
示例:
输入:nums = -2,1,-3,4,-1,2,1,-5,4
输出:6
解释:连续子数组 4,-1,2,1 的和最大为 6 。
对于连续子数组求和,先 想象 一些简单场景
- 场景一 :数组只有1个元素,那么最大和就1种情况 也就是
第1个元素; - 场景二 :数组扩展到2个元素,那么最大和就有3种情况了:
第1个元素、第1个元素+第2个元素、第2个元素。
对比场景一 与 场景二,由于第2个元素的出现 从而导致最大和子数组 可能包含第2个元素,从而新出现了:第1个元素+第2个元素、第2个元素两种情况,多出来的其实是:第2个元素作为子数组尾元素 的情况。
分析下 以第2个元素作为子数组尾元素 的最大和? 第2个元素 + 某个数 要最大,自然这里的 某个数 越大越好,因此它的一个选择就是 第2个元素 + 前一个元素(第1个元素)作为子数组尾元素的最大和 ; 但考虑到 某个数 可能为负数,所以 最大和还有一种选择 就是 第2个元素 了。
综上分析,以第2个元素作为子数组尾元素的最大和 就是在:以第1个元素作为数组尾元素最大和 + 第2个元素,第2个元素 中选一个较大的。
如果再加入第3个元素,以第3个元素作为子数组尾元素的最大和选择同理也是:第3个元素,第3个元素+以第2个元素作为子数组尾元素的最大和中选一个较大的。
依次类推第n个元素 a[n] 作为子数组尾元素的最大和 s[n],用公式来说就是:
s[n] = Max( a[n] , s[n-1] + a[n] )
所谓整个数组的最大和的连续子数组,无非是在 第1、第2...第n个元素结尾的 最大和 中选取最大的,这样也就完成题目的解答了。分析清楚了,代码实现上就比较简单了:
public int maxSubArray(int[] nums) {
int state = nums[0],max = state;
for(int i = 1; i < nums.length; i++){
// s[n] = Max(a[n], s[n-1] + a[n])
state = Math.max(nums[i],state + nums[i]);
max = Math.max( max , state );
}
return max;
}
可以看到解题的整个过程,从最简单基本的情况开始,一步一步推导到结果。这就是自底向上( Bottom-Up )的推导过程,实现上通常使用的是递推的编码方式。
阶段(Stage)、状态(State)、决策(Decision)
如果把推导 第1个元素、第2个元素...第n个元素结尾子数组最大和 看成一个个决策 阶段,s[n]可以看作第n个阶段决策后的 状态 ,所谓上题的 决策 就是指取最大值。这里值得注意点的是,第n个阶段决策只依赖于第n-1个阶段的状态。
以上就是动态规划中的三个重要概念:阶段、状态、决策。
-
阶段(Stage): 阶段表示解决问题的不同时间点或步骤。问题通常可以划分为多个阶段,每个阶段都对应于解决问题的一个关键步骤。动态规划算法通过逐个处理这些阶段来解决问题。 -
状态(State): 状态是描述问题局部情况的变量。在每个阶段,问题的状态会发生变化。动态规划算法的目标是定义状态,使得问题的解可以通过不同阶段的状态之间的转移关系来表示。状态是问题的关键抽象,对于不同的问题,状态的选择可能会有很大的差异。 -
决策(Decision): 决策是在每个阶段基于当前状态做出的选择。这些决策会影响问题的状态转移,从而影响问题的最终解。动态规划算法的关键之一是找到在每个阶段应该做出的最优决策,以达到整体问题的最优解。
对于递推公式: s[n] = Max(a[n], s[n-1] + a[n]),动态规划中也被称作 状态转移方程。
一般性解题步骤(General Problem-solving Steps)
如果非常细致的朋友会注意到,上述解题过程中最初用了 “ 想象 ” 一词;行文如此是为了更好的描述自底向上的过程。如果是解答一道从来没接触过的动态规划类算法题,通过“想象”推导分析出阶段来难度可能过高,当然不排除想象力丰富的朋友有此能力。
前文提到的阶段也好、决策也好都围绕的是状态;定义动态规划的状态是关键,可以说找到状态转移方程问题就已经解决了60%。这里给出一些一般性的解题步骤_参考_,以降低 “想象”的难度。
- 定义状态: 确定问题的状态,即描述问题局部情况的变量。状态的选择对问题的建模至关重要,不同的状态选择可能导致完全不同的动态规划解法。
- 找到状态转移方程: 对于每个状态,找到它与其他状态之间的关系,即状态转移方程。状态转移方程描述了问题从一个阶段到下一个阶段的转移规则,是动态规划问题的核心。
- 初始化: 定义问题的初始状态并进行初始化。
- 确定边界条件: 确定问题的边界条件,即在最小规模下直接解决问题的情况。这是递归或递推开始的基础,通常是问题的最小子问题。
- 计算顺序: 确定计算状态的顺序,也是划分阶段。可以采用自顶向下(Top-Down)的递归方法,也可以采用自底向上(Bottom-Up)的递推方法。
- 计算最终解: 根据 1-5 的分析结果进行编码,最终解通常是在问题的最后一个阶段计算得到的,它可能存储在动态规划表格的特定位置。
一些场景下可能需要记录路径或决策,如果需要记录最优解的具体路径或决策,可以在计算的过程中进行记录.当然,以上也只是建议的步骤并非一定要如此。
PS: 这里不妨多说一点状态,在上一篇中有提到过动态规划是最灵活的算法之一;灵活的原因就是面对不同问题状态设计的多样性;如果要想快速解出动态规划类题,还是需要多多练习,积累一些设计状态的经验。因此初学时不用太在意对比经验丰富的朋友,解决动态规划类效率较慢,差距可能只在于缺少各种状态设计的经验积累。
基本应用示例(Basic Examples)
LeetCode 122. 买卖股票的最佳时机 II【中等】
给你一个整数数组 prices ,其中 pricesi 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。返回 你能获得的 最大 利润 。
示例:
输入:prices = 1,2,3,4,5
输出:4
解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。总利润为 4 。
- 状态定义,preSell 定义为上一天没有持股情况下 最大利润,preBuy 定位为 持有股票情况下 最大利润。
- 状态转移方程:
currentSell = Max( preBuy + prices[i], preSell)
currentBuy = Max( preSell - prices[i], preBuy)
计算下一个状态时,current 也就变成了 pre。考虑到最终最大利润一定时 不持股情况,因此 max 只需记录过程中 currentSell 的最大值。
- 初始化以及边界条件,不持股下 preSell 为
0,持股下 买入了第一只股票 preBuy 为-prices[0]
public int maxProfit(int[] prices) {
int preSell = 0,preBuy = -prices[0];
int max = 0;
for(int i = 1; i < prices.length; i++){
int currentSell = Math.max(preSell,preBuy + prices[i]);
int currentBuy = Math.max(preBuy, preSell - prices[i]);
preSell = currentSell;
preBuy = currentBuy;
max = Math.max(currentSell,max);
}
return max;
}
LeetCode 198. 打家劫舍【中等】
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
示例:
- 输入:[1,2,3,1]
输出:4
解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。偷窃到的最高金额 = 1 + 3 = 4 。
这里可以体会下设计状态的经验,相信有 前一题的铺垫,对于这道题的状态设计就比较类似了。
- 定义状态,preSteal 前一夜偷了的最高金额,preNosteal 前一夜没偷的最高金额
- 状态转移方程:
nosteal = Max( preNosteal , preSteal )
steal = preNosteal + nums[i]
- 初始化以及边界条件,略
public int rob(int[] nums) {
int preSteal = nums[0],preNosteal = 0;
for(int i = 1; i < nums.length; i++){
int nosteal = Math.max(preNosteal,preSteal);
int steal = preNosteal + nums[i];
preSteal = steal;
preNosteal = nosteal;
}
return Math.max(preNosteal,preSteal);
}
LeetCode 377. 组合总和 Ⅳ【中等】
给你一个由 不同 整数组成的数组 nums ,和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。
题目数据保证答案符合 32 位整数范围。
示例:
输入:nums = 1,2,3, target = 4
输出:7
解释:所有可能的组合为:(1, 1, 1, 1)、(1, 1, 2)、(1, 2, 1)、(1, 3)、(2, 1, 1)、(2, 2)、(3, 1)。请注意,顺序不同的序列被视作不同的组合。
这个类似于01背包的问题,状态设计上也比较类似文章来源:https://www.toymoban.com/news/detail-746265.html
- 定义状态,
s[i]代表目标整数 i 时,组合的个数 - 状态转移方程:
对于整数 nums[j] , 如果 i >= nums[j] 代表有可能被 nums[j] 组成
相当于 s[ i-nums[j] ] 组合里面 都加上个 nums[j]元素 ,
所以s[i] 组合数新增了 s[ i-nums[j] ] 个。
s[i] += s[ i-nums[j] ]
- 初始化状态:s[0] 代表着不选取任何元素的是 target = 0,此时不选取任何元素为 唯一的方案。
public int combinationSum4(int[] nums, int target) {
int[] s = new int[target+1];
s[0] = 1;
for(int i = 1; i <= target; i++){
for(int j = 0; j < nums.length; j++){
if(i - nums[j] < 0) continue;
s[i] += s[i - nums[j]] ;
}
}
return s[target];
}
欢迎关注 Java研究者专栏、博客、公众号等文章来源地址https://www.toymoban.com/news/detail-746265.html
到了这里,关于数据结构与算法 | 动态规划算法(Dynamic Programming)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!