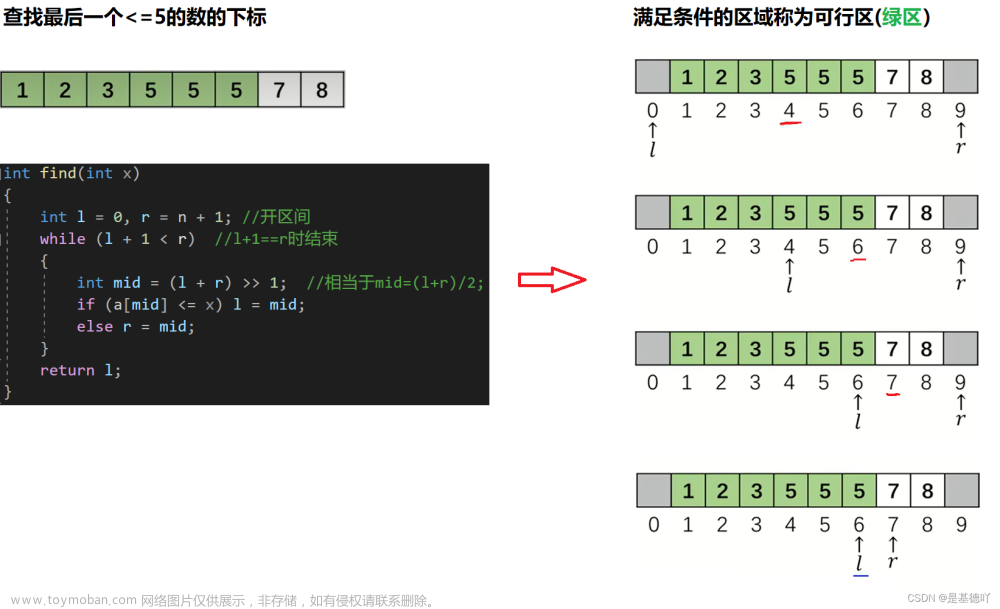
二分查找图解-Toy模板网

这篇具有很好参考价值的文章主要介绍了二分查找图解。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

二分查找图解

使用二分查找的前提是所给的元素集合必须是单调的。

注意：本文图文并茂

将提供以下图文链接供大家理解：
图文链接：
飞书图解链接🎉🎉🎉
密码：2k851&54

整数二分

查找最后一个小于等于q的元素的下标

模板代码，展开查看

int last(int q){
    int l = -1, r = n;
    while(l + 1 < r){
        int mid = l + r >> 1;
        if(a[mid] <= q) l = mid;
        else r = mid;
    }
    return l;
}

元素存在
返回对应元素的下标
元素不存在
返回最大小于该元素的元素的下标

查找第一个大于等于q的元素的下标

模板代码，展开查看

int first(int q){
    int l = -1, r = n;
    while(l + 1 < r){
        int mid = l + r >> 1;
        if(a[mid] >= q) r = mid;
        else l = mid;
    }
    return r;
}

元素存在
返回对应元素的下标
元素不存在
返回最小大于该元素的元素的下标

该模板具有对称之美，非常好记😊

习题一

AcWing 789. 数的范围

AC代码，展开查看

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int a[N];
int n, m, q;
int first(int q){ // 局部变量覆盖全局变量
    int l = -1, r = n;
    while(l + 1 < r){
        int mid = l + r >> 1;
        if(a[mid] >= q) r = mid;
        else l = mid;
    }
    return a[r] == q ? r : -1;
}
int last(int q){ // 局部变量覆盖全局变量
    int l = -1, r = n;
    while(l + 1 < r){
        int mid = l + r >> 1;
        if(a[mid] <= q) l = mid;
        else r = mid;
    }
    return a[l] == q ? l : -1;
}
int main(){
    scanf("%d%d", &n, &m);
    for(int i = 0; i < n; i ++ ) scanf("%d", &a[i]);
    while(m -- ){
        scanf("%d", &q);
        printf("%d %d\n", first(q), last(q));
    }
    return 0;
}

浮点数二分

最大化查找模板：

模板代码，展开查看

double find(double y){
    double l = -22, r = 22;
    while(r - l > pre){
        double mid = (l + r) / 2;
        if(mid * mid * mid <= y){
            l = mid;
        }else{
            r = mid;  
        }
    }
    return l;
}

最小化查找模板：

模板代码，展开查看

double find(double y){
    double l = -22, r = 22;
    while(r - l > pre){
        double mid = (l + r) / 2;
        if(mid * mid * mid >= y){
            r = mid;
        }else{
            l = mid;  
        }
    }
    return r;
}

习题一

AcWing 790. 数的三次方根

最大化AC代码，展开查看

#include<bits/stdc++.h>
using namespace std;
const double pre = 1e-8;
double find(double y){
    double l = -22, r = 22;
    while(r - l > pre){
        double mid = (l + r) / 2;
        if(mid * mid * mid <= y){
            l = mid;
        }else{
            r = mid;  
        }
    }
    return l;
}
int main(){
    double n;
    cin >> n;
    printf("%.6lf", find(n));
    return 0;
}

最小化AC代码，展开查看

#include<bits/stdc++.h>
using namespace std;
const double pre = 1e-8;
double find(double y){
    double l = -22, r = 22;
    while(r - l > pre){
        double mid = (l + r) / 2;
        if(mid * mid * mid >= y){
            r = mid;
        }else{
            l = mid;  
        }
    }
    return r;
}
int main(){
    double n;
    cin >> n;
    printf("%.6lf", find(n));
    return 0;
}

习题二

P2249 【深基13.例1】查找

AC代码，展开查看

#include<bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
int a[N];
int n, m, q;
int first(int q){ // 局部变量覆盖全局变量
    int l = -1, r = n;
    while(l + 1 < r){
        int mid = l + r >> 1;
        if(a[mid] >= q) r = mid;
        else l = mid;
    }
    return a[r] == q ? r + 1 : -1;
}
int main(){
    scanf("%d%d", &n, &m);
    for(int i = 0; i < n; i ++ ) scanf("%d", &a[i]);
    while(m -- ){
        scanf("%d", &q);
        printf("%d ", first(q));
    }
    return 0;
}

习题三

P1024 [NOIP2001 提高组] 一元三次方程求解

AC代码，展开查看

#include<bits/stdc++.h>
using namespace std;
const double pre = 1e-4;
double a, b, c, d;
double f(double x){ // 函数f(x)
    return a * x * x * x + b * x * x + c * x + d;
}
double find(double l, double r){
    while(r - l > pre){
        double mid = (l + r) / 2;
        if(f(mid) * f(r) < 0) l = mid;
        else r = mid;
    }
    return l;
}
int main(){
    cin >> a >> b >> c >> d;
    for(int i = -100; i < 100; i ++ ){ 
        double y1 = f(i), y2 = f(i + 1); // (-100, -99], (-99, -98],  ...,  (99, 100]: 排除根为100的情况
        if(!y2) printf("%.2lf ", i + 1.0); // 有可能该点正好是根
        if(y1 * y2 < 0) printf("%.2lf ", find(i, i + 1)); // 否则在(i, i + 1)区间二分根
    }
    return 0;
}

高效的牛顿法

牛顿法（英语：Newton's method）又称为牛顿-拉弗森方法（英语：Newton-Raphson method），它是一种在实数域和复数域上近似求解方程的方法。方法使用函数$f(x)$的泰勒级数的前面几项来寻找方程$f(x)=0$的根。

1. 方法说明

首先，选择一个接近函数$f(x)$零点的$x_{0}$，计算相应的$f(x_0)$和切线斜率$f'(x_0)$（这里$f'$表示函数$f$的导数）。然后我们计算穿过点$(x_{0},f(x_{0}))$并且斜率为$f'(x_0)$的直线和$x$轴的交点的$x$坐标，也就是求如下方程的解：
$$
{\displaystyle 0=(x-x_{0})\cdot f'(x_{0})+f(x_{0})}
$$
我们将新求得的点的$x$坐标命名为$x_1$，通常$x_1$会比$x_{0}$更接近方程$f(x)=0$的解。因此我们现在可以利用$x_1$开始下一轮迭代。迭代公式可化简为如下所示：
$$
{\displaystyle x_{n+1}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}}}
$$
已有证明牛顿迭代法的二次收敛必须满足以下条件：
$f'(x)\neq 0$; 对于所有$x\in I$，其中${\displaystyle I}$为区间$[α − r, α + r]$，且$x_{0}$在区间其中$I$内，即 $r\geqslant \left|a-x_{0}\right|$的;
对于所有${\displaystyle x\in I}$，$f''(x)$是连续的;
$x_{0}$足够接近根 $α$。

2. 案例

第一个案例：

求方程$\cos(x)-x^{3}=0$的根。令$f(x)=\cos(x)-x^{3}$，两边求导，得$f'(x)=-\sin(x)-3x^{2}$。由于$-1\leq \cos(x)\leq 1(\forall x)$，则$-1\leq x^{3}\leq 1$，即$-1\leq x\leq 1$，可知方程的根位于$0$和$1$之间。我们从${\displaystyle x_{0}=0.5}$开始。

第二个案例：

牛顿法亦可发挥与泰勒展开式，对于函式展开的功能。
求$a$的$m$次方根。
$x^{m}-a=0$

设$f(x)=x^{m}-a$，$f'(x)=mx^{m-1}$

而$a$的$m$次方根，亦是$x$的解，

以牛顿法来迭代：

\[x_{n+1}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}} \]

\[x_{n+1}=x_{n}-{\frac {x_{n}^{m}-a}{mx_{n}^{m-1}}} \]

\[x_{n+1}=x_{n}-{\frac {x_{n}}{m}}{(1-ax_{n}^{-m})} \]

（或 $$x_{n+1}=x_{n}-{\frac {1}{m}}\left(x_{n}-a{\frac {x_{n}}{x_{n}^{m}}}\right)$$）

3. 应用

求解最值问题

牛顿法也被用于求函数的极值。由于函数取极值的点处的导数值为零，故可用牛顿法求导函数的零点，其迭代式为

\[x_{n+1}=x_{n}-{\frac {f^{\prime }(x_{n})}{f^{\prime \prime }(x_{n})}} \]

求拐点的公式以此类推

引例：
用牛顿法求解平方根：

如果要求$S(S>1)$的平方根，选取$1 < x_{0} < S$

\[x_{n+1}={\frac {1}{2}}\left(x_{n}+{\frac {S}{x_{n}}}\right) \]

例子：求$\sqrt {125348}$至6位有效数字。

\[x_0 = 3^6 = 729.000 \]

\[x_1 = \frac{1}{2} \left(x_0 + \frac{S}{x_0}\right) = \frac{1}{2} \left(729.000 + \frac{125348}{729.000}\right) = 450.472 \]

\[x_2 = \frac{1}{2} \left(x_1 + \frac{S}{x_1}\right) = \frac{1}{2} \left(450.472 + \frac{125348}{450.472}\right) = 364.365 \]

\[x_3 = \frac{1}{2} \left(x_2 + \frac{S}{x_2}\right) = \frac{1}{2} \left(364.365 + \frac{125348}{364.365}\right) = 354.191 \]

\[x_4 = \frac{1}{2} \left(x_3 + \frac{S}{x_3}\right) = \frac{1}{2} \left(354.191 + \frac{125348}{354.191}\right) = 354.045 \]

\[x_5 = \frac{1}{2} \left(x_4 + \frac{S}{x_4}\right) = \frac{1}{2} \left(354.045 + \frac{125348}{354.045}\right) = 354.045 \]

因此$$\sqrt{125348} \approx 354.045$$

代码实现：

  package main
  import (
    "fmt"
  )
  func main() {
    // 求S = 125348的平方根
    // 1. 选取1 < x0 < S 
    // 	  x0 = 3^6 = 729.00
    // 2. 迭代5次
    var S float64 = 125348
    var x float64 = 729
    for i := 0; i < 5; i ++ {
      x = 1 / 2.0 * (x + S / x)
    }
    fmt.Printf("x: %v\n", x)
  }

结论:
不难看出

\[ x = \frac {1} {2} (x + \frac {S} {x}) \]

等价于：
在数学上是等价的，在计算机上$x^2$会超过int所表示的范围，变成+Inf

\[ x = \frac {x^2 + S} {2x} \]

将$x^2$，变为$2x^2 - x^2$，然后化简得

\[x = x - \frac {x^2 - S} {2x} \]

我们来推导出这个公式：

设$f(x) = x^2 - c \ (c \neq 0)$, $f'(x) = 2x$, $f''(x) = 2$
证明二次收敛:

$f'(x)\neq 0$; 对于所有$x\in I$，其中${\displaystyle I}$为区间$[1, c]$，设近似根为$x_0$，且$x_{0}$在区间$I$内;
对于所有${\displaystyle x\in I}$，$f''(x)$是连续的;
$x_{0}$足够接近根 $α$, $α$是实际的根。
根据定义将$x_0$，代入

\[0=(x-x_{0})\cdot f'(x_{0})+f(x_{0}) \]

因为二次收敛，所以等式两边除以$f'(x_{0})$，然后移项得

\[ x = x_0 - \frac {f(x_0)} {f'(x_0)} \]

则可以得到其迭代公式

\[ x_{n+1}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}} \]

代入求解得

\[ x_{n+1}=x_{n}-{\frac {x_n^2-c} {2x_{n}}} \]

推导完毕！

有了以上基础，下面就非常简单了

为了练习函数与循环，我们来实现一个平方根函数：用牛顿法实现平方根函数。

计算机通常使用循环来计算 $x$ 的平方根。从某个猜测的值 $z$ 开始，我们可以根据 $z^2$ 与 $x$ 的近似度来调整 $z$，产生一个更好的猜测：

\[z = z - \frac {z^2 - x} {2z} \]

重复调整的过程，猜测的结果会越来越精确，得到的答案也会尽可能接近实际的平方根。
在提供的 func Sqrt 中实现它。无论输入是什么，对 z 的一个恰当的猜测为 1。要开始，请重复计算 10 次并随之打印每次的 z 值。
观察对于不同的值 $x(1、2、3 ...)$ ，你得到的答案是如何逼近结果的，猜测提升的速度有多快。

提示：用类型转换或浮点数语法来声明并初始化一个浮点数值：

  z := 1.0
  z := float64(1)

然后，修改循环条件，使得当值停止改变（或改变非常小）的时候退出循环。观察迭代次数大于还是小于 10。尝试改变 z 的初始猜测，
如 x 或 x/2。你的函数结果与标准库中的 math.Sqrt 接近吗？

（注：如果你对该算法的细节感兴趣，上面的 z² − x 是 z² 到它所要到达的值（即 x）的距离，除以的 2z 为 z² 的导数，
我们通过 z² 的变化速度来改变 z 的调整量。这种通用方法叫做牛顿法。它对很多函数，特别是平方根而言非常有效。）

平方根函数

  package main
  import (
    "fmt"
    "math"
  )
  func Sqrt(x float64) float64 {
    // z最好在 1 < z < 2 内取值
    z := 1.5 // 迭代四次就够了
    for i :=  0; i < 4; i ++ {
      z -= (z * z - x) / (2 * z)
      fmt.Println(z)
    }
    return z
  }
  func main() {
    fmt.Println(Sqrt(2))
    fmt.Println("================")
    fmt.Println(math.Sqrt(2))
  }

同理再实现一个立方根函数

  package main
  import (
    "fmt"
  )
  func subtriplicate(x float64) float64 {
    z := 1.0
    for i := 0; i < 10; i ++ {
      z = z - z / 3.0 + x / (3.0 * z * z);
    }
    return z
  }
  func main() {
    fmt.Printf("subtriplicate(7): %v\n", subtriplicate(7))	
  }

总结：牛顿法收敛速度是二次方级别的，比二分法快多了

习题一

AcWing 790. 数的三次方根

AC代码，展开查看

#include<bits/stdc++.h>
using namespace std;
double cube(double x){
    double z = 1;
    for(int i = 0; i < 18; i ++ ){
        z = z - z / 3.0 + x / (3.0 * z * z);
    }
    return z;
}
int main(){
    double x;
    cin >> x;
    printf("%.6lf", cube(x));
    return 0;
}

二分答案

题目 1

LuoGu P2440 木材加工
样例:

2 6
11 21

AC代码，展开查看

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
int a[N];
int n, k;
bool check(int x){
    LL y = 0; // 段数
    for(int i = 0; i < n; i ++ ) y += a[i] / x;
    return y >= k;
}
int find(){
    int l = 0, r = 1e8 + 1; // x范围的开区间
    while(l + 1 < r){
        int mid = l + r >> 1;
        if(check(mid)) l = mid; // 满足条件，放大
        else r = mid;
    }
    return l;
}
int main(){
    scanf("%d%d", &n, &k);
    for(int i = 0; i < n; i ++ ) scanf("%d", &a[i]);
    printf("%d", find());
    return 0;
}

题目 2

P2678 [NOIP2015 提高组] 跳石头

AC代码，展开查看

#include<bits/stdc++.h>
using namespace std;
const int N = 5e4 + 10;
int a[N]; // a数组代表当前石头距离起点石头的距离(包含起点、终点的石头)
int l, n, m; // 起点到终点的距离，起点和终点之间的岩石数，至多移走的岩石数
bool check(int x){
    int y = 0; // 移掉的石头数
    for(int i = 1, pre = 0; i <= n + 1; i ++ ){
        // 如果当前石头与前一个石头的距离小于x则移除掉当前石头
        // 当当前石头是终点的石头的话，并且与前一个石头的距离小于x，
        // 则移除掉终点石头，这与移除掉前一个石头等价
        if(a[i] - a[pre] < x) y ++ ; 
        else pre = i; // 否则跳至下一个石头，前一个石头跳至当前石头
    }
    return y <= m;
}
int find(){
    int l = 0, r = 1e9 + 1; // 1 <= x << 1e9
    while(l + 1 < r){
        int mid = l + r >> 1;
        if(check(mid)) l = mid; // y <= M的话，增大x
        else r = mid;
    }
    return l;
}
int main(){
    scanf("%d%d%d", &l, &n, &m);
    for(int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
    // 起点到起点的距离为0
    // 终点到起点的距离为L
    a[n + 1] = l;
    printf("%d", find());
    return 0;
}

题目 3

Luogu P1314 [NOIP2011 提高组] 聪明的质监员

AC代码，展开查看

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 2e5 + 10;
int w[N], v[N], l[N], r[N];
LL sn[N], sv[N];  // 前缀和
LL s, ans = LONG_MAX; // 标准值、答案
int n, m; // 矿石的个数、区间的个数
bool check(int W){
    memset(sn, 0, sizeof sn);
    memset(sv, 0, sizeof sv); // 重复使用，清0
    for(int i = 1; i <= n; i ++ ){
        if(w[i] >= W) sn[i] = sn[i - 1] + 1, sv[i] = sv[i - 1] + v[i];
        else sn[i] = sn[i - 1], sv[i] = sv[i - 1];
    }
    LL y = 0;
    for(int i = 1; i <= m; i ++ ){
        y += (sn[r[i]] - sn[l[i] - 1]) * (sv[r[i]] - sv[l[i] - 1]);
    }
    ans = min(ans, abs(y - s)); // 不管最大化还是最小化，W每次二分的值都是一样的，所以结果也是一样的
    // return y <= s;
    return y >= s;
}
void find(){
    int l = 0, r = 1e6 + 1; // 0 < w <= 1e6
    while(l + 1 < r){
        int mid = l + r >> 1;
        // if(check(mid)) r = mid; // y <= s, 最小化w
        // else l = mid;
        if(check(mid)) l = mid; // y >= s, 最大化w
        else r = mid;
    }
}
int main(){
    scanf("%d%d%lld", &n, &m, &s);
    for(int i = 1; i <= n; i ++ ) scanf("%d%d", &w[i], &v[i]);
    for(int i = 1; i <= m; i ++ ) scanf("%d%d", &l[i], &r[i]);
    find();
    printf("%lld", ans);
    return 0;
}

题目 4

Luogu P1083 [NOIP2012 提高组] 借教室

AC代码，展开查看

#include<bits/stdc++.h>
using namespace std;
typedef long long LL; // 由于使用前缀和, 第i天需要用的教室数量之和会溢出 INT_MAX
const int N = 1e6 + 10;
int r[N], d[N], s[N], t[N]; // 第i天可用于租借的教室数量、租借的数量，租借开始、结束分别在第几天。
int n, m; // 表示天数和订单的数量。
LL a[N]; // 第i天需要用的教室数量之和
bool check(int x){
    memset(a, 0, sizeof a);
    for(int i = 1; i <= x; i ++ ) a[s[i]] += d[i], a[t[i] + 1] -= d[i];
    for(int i = 1; i <= n; i ++ ){
        a[i] += a[i - 1];
        if(a[i] > r[i]) return false;
    }
    return true;
}
int find(){
    int l = 0, r = m + 1; // 1 <= x <= m
    while(l + 1 < r){
        int mid = l + r >> 1;
        if(check(mid)) l = mid; // 满足条件，放大 x
        else r = mid;
    }
    return l;
}
int main(){
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i ++ ) scanf("%d", &r[i]);
    for(int i = 1; i <= m; i ++ ) scanf("%d%d%d", &d[i], &s[i], &t[i]);
    int ans = find();
    if(ans == m) puts("0");
    else printf("-1\n%d", ans + 1);
    return 0;
}

题目 5

Luogu P1902 刺杀大使

AC代码，展开查看

#include<bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10;
int n, m, p[N][N];
bool vis[N][N];
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1}; // 上右下左
bool dfs(int x, int y, int P){
    if(x == n) return true; // 到达第n行,通过迷宫返回true
    vis[x][y] = true; // 该坐标走过
    for(int i = 0; i < 4; i ++ ){
        // 深搜其他点
        int a = x + dx[i], b = y + dy[i];
        if(a >= 1 && a <= n && b >= 1 && b <= m && !vis[a][b] && p[a][b] <= P)
            if(dfs(a, b, P)) return true;
    }
    // 走不到第n行，原路返回，返回false
    return false;
}
int find(){
    int l = -1, r = 1e3 + 1; // 0 <= x <= 1000
    while(l + 1 < r){
        int mid = l + r >> 1;
        memset(vis, 0, sizeof vis); // 重置标记数组
        if(dfs(1, 1, mid)) r = mid; // 满足条件，x尽可能小
        else l = mid;
    }
    return r;
}
int main(){
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i ++ ){
        for(int j = 1; j <= m; j ++ ){
            scanf("%d", &p[i][j]);
        }
    }
    printf("%d", find());
}

题目 6

Luogu P1163 银行贷款

AC代码，展开查看

#include<bits/stdc++.h>
using namespace std;
const double pre = 1e-5;
int w0, w, m;
bool check(double x){
    double s = w0;
    for(int i = 1; i <= m; i ++ ) s = s * (1 + x) - w;
    return s >= 0; // 如果没有还完钱，则说明利率太大，缩小范围(最大化，最小化均可以)
}
double find(){
    double l = 0, r = 10; // 利率大致范围
    while(r - l > pre){
        double mid = (l + r) / 2;
        if(check(mid)) r = mid;
        else l = mid;
    }
    return r;
}
int main(){
    scanf("%d%d%d", &w0, &w, &m);
    printf("%.1lf", find() * 100); // 百分比
    return 0;
}