前缀和、差分
前缀和可以快速求区间和。
差分相当于前缀和的逆运算。
前缀和、差分都是以空间换时间的算法
注意:本文图文并茂
将提供以下图文链接供大家理解:
图文链接:
飞书图解链接🎉🎉🎉
密码:67&2Z172
前缀和
定义
前缀和可以简单理解为「数列的前 n 项的和」,是一种重要的预处理方式,能大大降低查询的时间复杂度。
一维前缀和
题目一
Luogu P8218 【深进1.例1】求区间和
AC代码,展开查看
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int a[N], s[N];
int main(){
int n, m;
scanf("%d", &n);
for(int i = 1; i <= n; i ++ ) {
scanf("%d", &a[i]);
s[i] = s[i - 1] + a[i];
}
scanf("%d", &m);
while(m -- ){
int l, r;
scanf("%d%d", &l, &r);
printf("%d\n", s[r] - s[l - 1]);
}
return 0;
}
题目二
Acwing 795. 前缀和
AC代码,展开查看
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int a[N], s[N];
int main(){
int n, m, l, r;
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i ++ ) {
scanf("%d", &a[i]);
s[i] = s[i - 1] + a[i];
}
while(m -- ){
scanf("%d%d", &l, &r);
printf("%d\n", s[r] - s[l - 1]);
}
return 0;
}
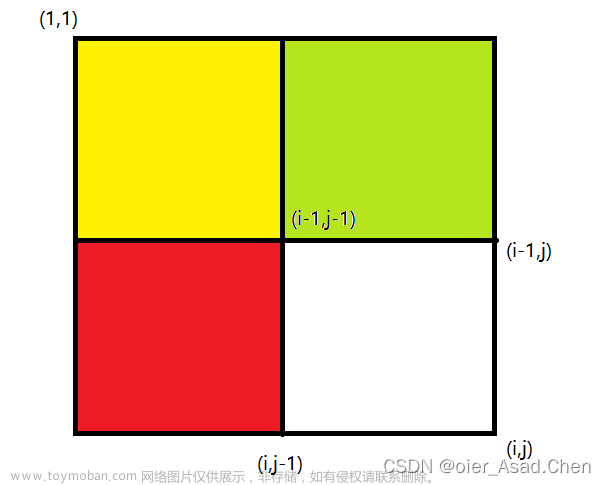
二维前缀和
题目一
AcWing 796. 子矩阵的和
AC代码,展开查看
#include<bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10;
int n, m, q;
int a[N][N];
int main(){
scanf("%d%d%d", &n, &m, &q);
for(int i = 1; i <= n; i ++ ){
for(int j = 1; j <= m; j ++ ){
scanf("%d", &a[i][j]);
a[i][j] += a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1];
}
}
int x1, y1, x2, y2;
while(q -- ){
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
printf("%d\n", a[x2][y2] - a[x2][y1 - 1] - a[x1 - 1][y2] + a[x1 - 1][y1 - 1]);
}
return 0;
}
题目二
Luogu P2280 [HNOI2003] 激光炸弹
AC代码,展开查看
#include<bits/stdc++.h>
using namespace std;
const int N = 5e3 + 2;
int s[N][N];
int main(){
int n, m, x, y, v;
scanf("%d%d", &n, &m);
for(int i = 0; i < n; i ++ ){
scanf("%d%d%d", &x, &y, &v);
x ++ , y ++ ;
s[x][y] += v; // 每个攻击目标都具有v价值,攻击目标有可能重复
}
for(int i = 1; i < N; i ++ ){
for(int j = 1; j < N; j ++ ){
s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
}
}
int res = 0;
for(int i = m; i < N; i ++ ){
for(int j = m; j < N; j ++ ){
res = max(res, s[i][j] - s[i - m][j] - s[i][j - m] + s[i - m][j - m]);
}
}
printf("%d", res);
return 0;
}
差分
定义
差分是一种和前缀和相对的策略,可以当做是求和的逆运算。
一维差分
题目一
Acwing 797. 差分
AC代码,展开查看
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int a[N];
int main(){
int n, m, l, r, c, t;
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i ++ ){
scanf("%d", &t);
a[i] += t; // 求差分数组, 相当于b[i] = a[i] - a[i - 1];
a[i + 1] -= t;
}
while(m -- ){
scanf("%d%d%d", &l, &r, &c);
a[l] += c;
a[r + 1] -= c;
}
for(int i = 1; i <= n; i ++ ){
a[i] += a[i - 1];
printf("%d ", a[i]);
}
}
题目二
Luogu P4552 [Poetize6] IncDec Sequence
AC代码,展开查看
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
int a[N];
int main(){
int n, t;
scanf("%d", &n);
for(int i = 0; i < n; i ++ ){
scanf("%d", &t);
a[i] += t, a[i + 1] -= t;
}
LL p = 0, q = 0;
for(int i = 1; i < n; i ++ ){
if(a[i] > 0) p += a[i]; // 正数总和
else q += a[i]; // 负数总和
}
q = abs(q); // 求负数总和的绝对值
printf("%ld\n%ld", max(p, q), abs(p - q) + 1);
return 0;
}
二维差分
题目一
AcWing 798. 差分矩阵
解法一:
AC代码,展开查看
#include<bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10;
int a[N][N];
int main(){
int n, m, q, x1, y1, x2, y2, c, t;
scanf("%d%d%d", &n, &m, &q);
for(int i = 1; i <= n; i ++ ){
for(int j = 1; j <= m; j ++ ){
scanf("%d", &t);
a[i][j] += t, a[i][j + 1] -= t;
}
}
while(q -- ){
scanf("%d%d%d%d%d", &x1, &y1, &x2, &y2, &c);
for(int i = x1; i <= x2; i ++ ){
a[i][y1] += c, a[i][y2 + 1] -= c;
}
}
for(int i = 1; i <= n; i ++ ){
for(int j = 1; j <= m; j ++ ){
a[i][j] += a[i][j - 1];
printf("%d ", a[i][j]);
}
puts("");
}
return 0;
}
这种方法本质上是一维差分,可以AC,但是花费3s
解法二:
AC代码,展开查看
#include<bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10;
int a[N][N];
void insert(int x1, int y1, int x2, int y2, int c){
a[x1][y1] += c;
a[x2 + 1][y1] -= c;
a[x1][y2 + 1] -= c;
a[x2 + 1][y2 + 1] += c;
}
int main(){
int n, m, q, t;
scanf("%d%d%d", &n, &m, &q);
for(int i = 1; i <= n; i ++ ){
for(int j = 1; j <= m; j ++ ){
scanf("%d", &t);
insert(i, j, i, j, t);
}
}
int x1, y1, x2, y2, c;
while(q -- ){
scanf("%d%d%d%d%d", &x1, &y1, &x2, &y2, &c);
insert(x1, y1, x2, y2, c);
}
for(int i = 1; i <= n; i ++ ){
for(int j = 1; j <= m; j ++ ){
a[i][j] += a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1];
printf("%d ", a[i][j]);
}
puts("");
}
return 0;
}
题目二
Luogu P3397 地毯
解法1:
AC代码,展开查看
#include<bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10;
int a[N][N];
int main(){
int n, m, x1, y1, x2, y2;
scanf("%d%d", &n, &m);
while(m -- ){
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
for(int i = x1; i <= x2; i ++ ){
a[i][y1] ++ , a[i][y2 + 1] -- ;
}
}
for(int i = 1; i <= n; i ++ ){
for(int j = 1; j <= n; j ++ ){
a[i][j] += a[i][j - 1];
printf("%d ", a[i][j]);
}
puts("");
}
return 0;
}
解法2:
AC代码,展开查看
#include<bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10;
int a[N][N];
void insert(int x1, int y1, int x2, int y2, int c){
a[x1][y1] += c;
a[x2 + 1][y1] -= c;
a[x1][y2 + 1] -= c;
a[x2 + 1][y2 + 1] += c;
}
int main(){
int n, m, x1, y1, x2, y2;
scanf("%d%d", &n, &m);
while(m -- ){
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
insert(x1, y1, x2, y2, 1);
}
for(int i = 1; i <= n; i ++ ){
for(int j = 1; j <= n; j ++ ){
a[i][j] += a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1];
printf("%d ", a[i][j]);
}
puts("");
}
return 0;
}
第二种方法更快,快了1ms.🤣
本文参考自【董晓算法的个人空间-哔哩哔哩】文章来源:https://www.toymoban.com/news/detail-747028.html
海纳百川,有容乃大!如果文章有什么不足之处,还请大神们评论区留言指出,我在此表达感谢🥰!若大家喜欢我的作品,欢迎点赞、收藏、打赏🎉🎉🎉!文章来源地址https://www.toymoban.com/news/detail-747028.html
到了这里,关于前缀和、差分的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!