scipy.stats子模块包含大量的概率分布、汇总和频率统计、相关函数和统计测试、掩蔽统计、核密度估计、准蒙特卡罗功能等等。
这个子模块可以帮助我们描述和分析数据,进行假设检验和拟合统计模型等。
1. 主要功能
具体来说,scipy.stats子模块包括以下主要功能:
| 类别 | 说明 |
|---|---|
| 连续统计分布 | 包括正态分布、指数分布、卡方分布、t分布、F分布等常见的连续概率分布。这些分布都有各自的密度函数、分布函数、累积函数、随机生成器和统计特性等。 |
| 分段统计分布 | 包括伯努利分布、二项分布、泊松分布、正态分布、指数分布等常见的离散概率分布。这些分布都有各自的密度函数、分布函数、累积函数、随机生成器和统计特性等。 |
| 统计测试 | 包括t检验、方差分析、卡方检验、相关系数检验、回归分析等常见的统计测试方法。这些测试方法可以用于假设检验和数据分析。 |
| 拟合统计模型 | 包括线性回归、逻辑回归、岭回归等常见的回归模型,以及广义线性模型等复杂模型。这些模型可以用于数据拟合和预测。 |
| 其他功能 | 包括分布的随机生成、分位数生成、随机变量的数字特征计算、矩母函数等其他实用功能。 |
2. 统计分布示例
下面演示几个通过scipy.stats子模块构建的统计分布的示例。
2.1. 多项式分布
多项式分布是一种离散型概率分布,用于描述在n次独立重复试验中,每次试验中k个不同的结果出现的概率。其中n表示试验次数,k表示要发生的结果数。
多项式分布主要用于描述在实际问题中一些离散型随机变量的概率分布,
例如人类的寿命、产品的寿命、遗传学中的多基因效应、网络中的链接数等。
构建一个多项式分布的示例:
\(f(x_1,x_2,...,x_k;p_1,p_2,...,p_k,n)=\frac{n!}{x_1!...x_k!}p_1^{x_1}p_2^{x_2}...p_k^{x_k}\)
from scipy.stats import multinomial
N = 5
p = np.ones(N)/N
# 计算概率质量函数
multinomial.pmf([N,0,0,0,0], n=N, p=p)
# 基于参数n和p,从多项分布中抽取随机样本
multinomial.rvs(n=100, p=p, size=5)
# 运行结果:
array([[25, 17, 16, 23, 19],
[16, 23, 23, 19, 19],
[19, 24, 14, 20, 23],
[19, 22, 27, 16, 16],
[15, 11, 30, 23, 21]])
size就是随机样本的个数,相当于返回的二维数组的行数。
每行数据的数目就是参数p的长度(也就是代码中的N)。
每行数据加起来的和就是 参数n(上面的示例中,二维数组每行加起来的和是100)
2.2. \(\beta\)分布
\(\beta\)分布是一种连续型概率分布,用于描述区间[0,1]内某一随机变量的概率分布形态。
\(\beta\)分布的概率密度函数由两个参数α和β确定,它们分别控制分布的左端点和右端点以及分布的形状。
\(\beta\)分布主要用于描述在实际问题中一些变量在区间[0,1]内的概率分布形态,
例如人类的能力、测试的得分、金融市场的收益率等。
构建一个\(\beta\)分布的示例:
\(\begin{align*}
f(x;a,b) = \frac{\varGamma(a+b)x^{a-1}(1-x)^{b-1}}{\varGamma(a)\varGamma(b)} \quad\quad 0 \le x \le 1
\end{align*}\)
from scipy.stats import beta
# 三种不同的 a,b 系数,分别为:
# a<b; a==b; a>b
params = [(1.5, 5.5), (5.5, 5.5), (5.5, 1.5)]
for p in params:
a, b = p
mean, var, skew, kurt = beta.stats(a, b, moments="mvsk")
print(
"平均数:{:.2f}, 方差:{:.2f}, 偏态:{:.2f}, 峰度系数:{:.2f}".format(
mean,
var,
skew,
kurt,
)
)
# 运行结果:
平均数:0.21, 方差:0.02, 偏态:0.88, 峰度系数:0.43
平均数:0.50, 方差:0.02, 偏态:0.00, 峰度系数:-0.43
平均数:0.79, 方差:0.02, 偏态:-0.88, 峰度系数:0.43
三种不同的分布绘制成图形的话:
from scipy.stats import beta
import numpy as np
import matplotlib.pyplot as plt
params = [(1.5, 5.5), (5.5, 5.5), (5.5, 1.5)]
labels = ["a=1.5,b=5.5", "a=5.5,b=5.5", "a=5.5,b=1.5"]
for idx, p in enumerate(params):
a, b = p
x = np.linspace(beta.ppf(0, a, b), beta.ppf(1, a, b), 100)
plt.plot(x, beta.pdf(x, a, b),label=labels[idx])
plt.legend(loc="upper center")
plt.show()

从图中可以体会,a, b两个参数对分布的影响。
2.3. 高斯分布
高斯分布,也称为正态分布(Normal distribution),是一种连续概率分布,在自然界和社会科学领域中广泛存在。
它的概率密度函数呈钟形曲线,两头低,中间高,左右对称,因此也被称为钟形曲线。
高斯分布主要用于描述许多自然现象和社会科学中的概率分布形态,
例如人类的身高、人类的智商、动物的寿命、人类的寿命、产品的寿命、遗传学中的多基因效应、网络中的链接数等。
构建一个高斯分布的示例:
\(\begin{align*}
f(x;\mu,\sigma)=\frac{1}{\sqrt{2\pi\sigma^2}}exp(-\frac{(x-\mu)^2}{\sigma^2}) \quad\quad -\infty \lt x \le \infty
\end{align*}\)
from scipy.stats import norm
params = [(1, 2),(2, 2),(2, 1)]
for p in params:
mu, sigma = p
mean, var = norm.stats(loc=mu, scale=sigma, moments='mv')
print(
"平均数:{:.2f}, 方差:{:.2f}".format(
mean,
var,
)
)
# 运行结果:
平均数:1.00, 方差:4.00
平均数:2.00, 方差:4.00
平均数:2.00, 方差:1.00
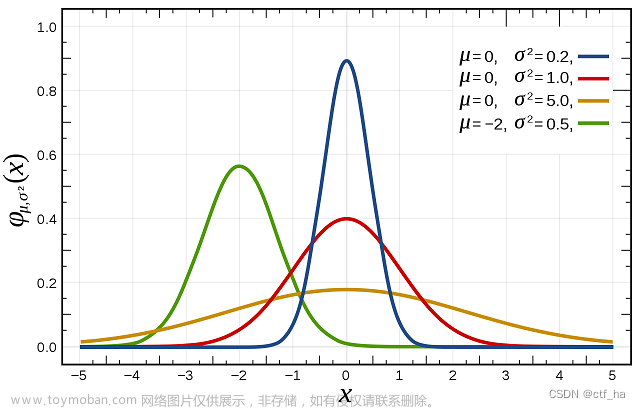
从运行结果可以看出,\(\mu\)参数会影响结果的平均数;\(\sigma\)参数则影响结果的方差。
将结果绘制成图形更好理解一些:
from scipy.stats import norm
import matplotlib.pyplot as plt
params = [(1, 2),(2, 2),(2, 1)]
labels = ["mu=1,sigma=2", "mu=2,sigma=2", "mu=2,sigma=1"]
for idx, p in enumerate(params):
mu, sigma = p
x = np.linspace(norm.ppf(0.01, mu, sigma), norm.ppf(0.99, mu, sigma), 100)
plt.plot(x, norm.pdf(x, mu, sigma), label=labels[idx])
plt.legend(loc="upper left")
plt.show()

从图中来看,\(\mu\)参数控制图形左右偏移程度,\(\sigma\)参数控制图形的陡峭程度。
3. 总结
总之,scipy.stats子模块为统计学和数据分析提供了丰富的工具和函数,可以帮助我们进行各种统计分析和数据处理任务。文章来源:https://www.toymoban.com/news/detail-747773.html
不过,统计是一个非常大的领域,其中有些主题还是超出了 SciPy 的范围,并被其他Python软件包涵盖。
比如其中一些比较著名的是statsmodels,PyMC,scikit-learn等等。
遇到scipy.stats难以处理的问题时,可以看看这些库中是否已经有解决方案。文章来源地址https://www.toymoban.com/news/detail-747773.html
到了这里,关于【scipy 基础】--统计分布的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!