1.7 前缀、中缀、后缀表达式
1.7.1 概念
-
它们都是对表达式的记法,因此也被称为前缀记法、中缀记法和后缀记法。它们之间的区别在于运算符相对与操作数的位置不同
- 前缀表达式的运算符位于与其相关的操作数之前;中缀和后缀同理。
- 平时我们日常使用并最为熟悉的就是中缀表达式。如:1 + 2 * 3 + 5 / 1 - 5;
- 后缀表达式又称为逆波兰式
-
优先级:从大到小是()> */ > ±
-
一个式子: a(b+c)-d*
- 中缀表达式(默认):a(b+c)-d*
- 前缀表达式: *-a+bcd
- 后缀表达式: *abc+d-
1.7.1 前、中、后缀表达式之间的转换思路
-
中缀表达式转换为前缀表达式
转化的时候先转化优先级大的式子,然后将转化完式子的当做一个整体的操作数来看待,可以将原中缀表达式按照优先级全部加上括号后再转换可能会好理解一点
比如:a ( b + c ) - d —> ( ( a ( b + c ) - d ) —> - * a + b c d* -
中缀表达式转换为后缀表达式
操作步骤与 中缀表达式转前缀表达式差不多。只不过操作符位置变成了2个操作数后面了
比如: a ( b + c ) - d —> a b c + * d -
-
前缀表达式转换为中缀表达式
比如:- * a + b c d **
利用栈的思想** 从右向左扫描前缀表达式,扫描到数字入栈,扫描到操作符,出栈2个数字与操作符计算后再将结果入栈,直到表达式扫描结束 -
后缀表达式转换为中缀表达式
比如:a b c + * d -
利用栈的思想 从左向右扫描前缀表达式,扫描到数字入栈,扫描到操作符,出栈2个数字与操作符计算后再将结果入栈,直到表达式扫描结束
1.7.2 实现逆波兰式计算器(后缀表达式)
思路:
-
1.扫描字符串 将字符挨个加入到一个list<String> ls内
-
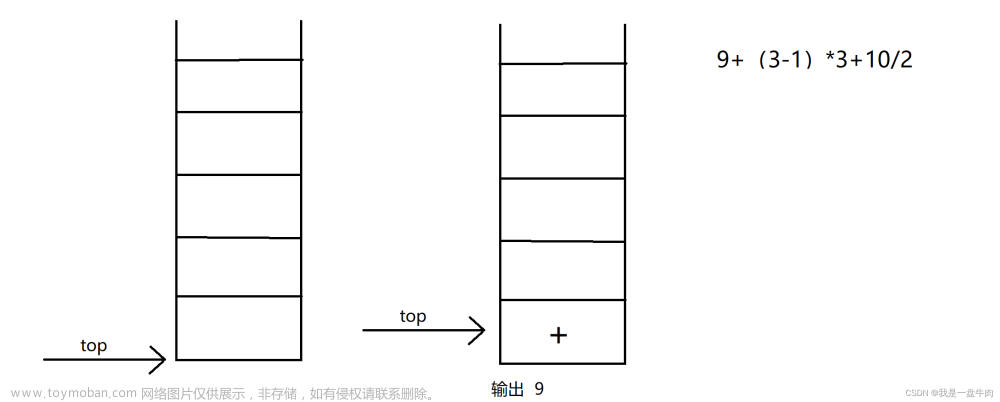
2.从左至右扫描后缀表达式ls 遇到数字入堆栈。遇到符号时候弹出栈顶两个数 用运算符对它们进行计算 并将结果入栈 重复上诉过程直到表达式最左端 最后的栈内留下的值就是计算的结果
-
3.在扫描ls中 需要判断是否为数字 可以使用正则判断(s.matches(“\\d+”)),也可以将字符转化为数字类型再判断
说明:
- 1.逆波兰表达式其实就是后缀表达式
- 2.本代码目的是为了说明数据结构 在设计上暂时不支持对小数的计算 如果要加上对小数的计算 只要加上对小数的判断即可
- 3.为了简化扫描表达式的判断 设置后缀表达式字符串数字之间需要空格隔开(不隔开也行,不过这样就需要在扫描的时候额外添加一个多位数字的扫描判断)
比如 : 1 + 2 + 3 + 4 * 5
实现核心代码:
扫描字符串加入到列表
public static List<String> scanExpression(String expression){
// 扫描字符串表达式 将字符与数字加入到列表内
List<String> ls = new ArrayList<>();
String[] s = expression.split(" ");
Collections.addAll(ls, s);
return ls;
}
计算后缀表达式
public static int PostfixExpressionCalculator(List<String> ls){ // 开始计算后缀表达式
Stack<String> stack = new Stack<>();
for (String s: ls){
if (s.matches("\\d++")){ // 使用正则表达式识别数字字符
stack.push(s);
continue;
}
String num1 = stack.pop();
String num2 = stack.pop();
int result = count1(num1, num2, s);
stack.push(String.valueOf(result)); // 将运算结果入栈
}
return Integer.parseInt(stack.pop());
}
计算运算符与操作数结果
public static int count1(String num1,String num2,String p1){ // 遇到符号时的运算
int n1 = Integer.parseInt(num1);
int n2 = Integer.parseInt(num2);
switch (p1){
case "+": return n1+n2;
case "-": return n2-n1;
case "*": return n1*n2;
case "/": return n2/n1;
default:
throw new RuntimeException("出现无法识别的运算符!");
}
}
测试表达式:String test = “1 2 3 + * 40 -”;
输出结果:
引申:
- 前缀表达式的计算与后缀表达式的计算大同小异,只是扫描表达式的方向变为了从右向左
// 前缀表达式计算函数
public static int prefixExpressionCalculator(List<String> ls){
Stack<String> stack = new Stack<>();
for (int i = ls.size()-1;i>=0;i--){
String s = ls.get(i);
if (s.matches("\\d++")){ // 使用正则表达式识别数字字符
stack.push(s);
continue;
}
// 注意前缀表达式的num1与num2的顺序与后缀表达式 是相反的
String num1 = stack.pop();
String num2 = stack.pop();
int result = count1(num2, num1, s);
stack.push(String.valueOf(result)); // 将运算结果入栈
}
return Integer.parseInt(stack.pop());
}
测试表达式:String test2 = “- * + 2 3 1 4”; // 1(2+3)-4 = 1*
输出结果:
中缀表达式的计算器实现在另外一片文章内已经写好了
https://blog.csdn.net/m0_52861211/article/details/129865965?spm=1001.2014.3001.5502
1.7.3 中缀表达式转化为后缀表达式
对于人类来说,中缀表达式的计算是很符合思考逻辑的。但是对于计算机来说,中缀表达式的计算相比后缀表达式和前缀表达的计算很是繁琐,所以我们可以先设计方法将中缀表达式转化为后缀表达式/前缀表达式再计算。
思路:

实现代码:
返回运算符的优先级
public static int checkOrder(String str){ // 返回运算符的优先级
switch (str) {
case "/":
case "*" : return 2;
case "-":
case "+" : return 0;
default : return -1;
}
}
判断字符是否是运算符
public static boolean isOperator(String operator){ // 判断字符是否是运算符
return ("+".equals(operator)||"-".equals(operator)||"*".equals(operator)||"/".equals(operator));
}
将中缀表达式转换为后缀表达式
// 实现中缀表达式转化为后缀表达式
// 因为s2这个栈 在整个过程中没有弹出栈的操作,而且最终结果是s2栈的逆序输出结果 所以可以使用list来代替栈实现 简化输出
public static List<String> Infix2PostfixExpression(String str){
// 1. 扫描表达式
List<String> ls = scanExpression(str);
// 2. 初始化s1 s2
Stack<String> s1 = new Stack<>(); // 运算符栈
List<String> s2 = new ArrayList<>(); // 结果集合
// 3. 开始转化
for(String tempS : ls){
// 3.1操作数直接入s2
if (tempS.matches("\\d+")){
s2.add(tempS);
} else if (isOperator(tempS)) { // 3.2 遇到运算符
while (true){
// 栈空或栈顶元素为 ( ,直接将当前符号入栈
if (s1.isEmpty()||s1.peek().equals("(")){
s1.push(tempS);
break;
}
if (checkOrder(tempS) > checkOrder(s1.peek())){ // 优先级大于栈顶运算符,入栈
s1.push(tempS);
break;
}// 否则 s1栈顶弹出压入s2 重新判断与新栈顶的优先级
String pop = s1.pop();
s2.add(pop);
}
}else{ // 3.3 遇到括号
if ("(".equals(tempS)){ // 遇到左括号 直接压入s1
s1.push(tempS);
}else if (")".equals(tempS)){ // 遇到右括号
// 依次弹出s1栈顶的运算符,并压入s2 直到遇到栈顶元素为左括号为止 最后把这一对括号都丢弃
while (!"(".equals(s1.peek())){
s2.add(s1.pop());
}
s1.pop(); // 将右括号弹出
}else
throw new RuntimeException("输入运算符有误!无法识别!");
}
}
// 在表达式扫描完毕后 将s1中剩余的运算符依次弹出并压入s2
while (s1.size() != 0)
s2.add(s1.pop());
// s2顺序输出就是转换后的后缀表达式了
return s2;
}
1.7.4 全部完整代码与输出结果
代码:文章来源:https://www.toymoban.com/news/detail-751526.html
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
import java.util.Stack;
public class PostfixExpressionCalculatorDemo {
public static List<String> scanExpression(String expression){
// 扫描字符串表达式 将字符与数字加入到列表内
List<String> ls = new ArrayList<>();
String[] s = expression.split(" ");
Collections.addAll(ls, s);
return ls;
}
// 实现中缀表达式转化为后缀表达式
// 因为s2这个栈 在整个过程中没有弹出栈的操作,而且最终结果是s2栈的逆序输出结果 所以可以使用list来代替栈实现 简化输出
public static List<String> Infix2PostfixExpression(String str){
// 1. 扫描表达式
List<String> ls = scanExpression(str);
// 2. 初始化s1 s2
Stack<String> s1 = new Stack<>(); // 运算符栈
List<String> s2 = new ArrayList<>(); // 结果集合
// 3. 开始转化
for(String tempS : ls){
// 3.1操作数直接入s2
if (tempS.matches("\\d+")){
s2.add(tempS);
} else if (isOperator(tempS)) { // 3.2 遇到运算符
while (true){
// 栈空或栈顶元素为 ( ,直接将当前符号入栈
if (s1.isEmpty()||s1.peek().equals("(")){
s1.push(tempS);
break;
}
if (checkOrder(tempS) > checkOrder(s1.peek())){ // 优先级大于栈顶运算符,入栈
s1.push(tempS);
break;
}// 否则 s1栈顶弹出压入s2 重新判断与新栈顶的优先级
String pop = s1.pop();
s2.add(pop);
}
}else{ // 3.3 遇到括号
if ("(".equals(tempS)){ // 遇到左括号 直接压入s1
s1.push(tempS);
}else if (")".equals(tempS)){ // 遇到右括号
// 依次弹出s1栈顶的运算符,并压入s2 直到遇到栈顶元素为左括号为止 最后把这一对括号都丢弃
while (!"(".equals(s1.peek())){
s2.add(s1.pop());
}
s1.pop(); // 将右括号弹出
}else
throw new RuntimeException("输入运算符有误!无法识别!");
}
}
// 在表达式扫描完毕后 将s1中剩余的运算符依次弹出并压入s2
while (s1.size() != 0)
s2.add(s1.pop());
// s2顺序输出就是转换后的后缀表达式了
return s2;
}
public static int PostfixExpressionCalculator(List<String> ls){ // 开始计算后缀表达式
Stack<String> stack = new Stack<>();
for (String s: ls){
if (s.matches("\\d++")){ // 使用正则表达式识别数字字符
stack.push(s);
continue;
}
String num1 = stack.pop();
String num2 = stack.pop();
int result = count1(num1, num2, s);
stack.push(String.valueOf(result)); // 将运算结果入栈
}
return Integer.parseInt(stack.pop());
}
public static int prefixExpressionCalculator(List<String> ls){
Stack<String> stack = new Stack<>();
for (int i = ls.size()-1;i>=0;i--){
String s = ls.get(i);
if (s.matches("\\d++")){ // 使用正则表达式识别数字字符
stack.push(s);
continue;
}
// 注意前缀表达式的num1与num2的顺序与后缀表达式 是相反的
String num1 = stack.pop();
String num2 = stack.pop();
int result = count1(num2, num1, s);
stack.push(String.valueOf(result)); // 将运算结果入栈
}
return Integer.parseInt(stack.pop());
}
public static int count1(String num1,String num2,String p1){ // 遇到符号时的运算
int n1 = Integer.parseInt(num1);
int n2 = Integer.parseInt(num2);
switch (p1){
case "+": return n1+n2;
case "-": return n2-n1;
case "*": return n1*n2;
case "/": return n2/n1;
default:
throw new RuntimeException("出现无法识别的运算符!");
}
}
public static int checkOrder(String str){ // 返回运算符的优先级
switch (str) {
case "/":
case "*" : return 2;
case "-":
case "+" : return 0;
default : return -1;
}
}
public static boolean isOperator(String operator){ // 判断字符是否是运算符
return ("+".equals(operator)||"-".equals(operator)||"*".equals(operator)||"/".equals(operator));
}
public static void main(String[] args) {
// 后缀表达式1
String test = "1 2 3 + * 40 -"; // 1*(2+3)-40 = -35
// 前缀表达式2
String test2 = "- * + 2 3 1 4"; // 1*(2+3)-4 = 1
// 中缀表达式3
String test3 = "1 + ( ( 2 + 3 ) * 4 ) - 5"; // 16
List<String> ls = scanExpression(test);
List<String> ls2 = scanExpression(test2);
System.out.println("后缀表达式1: "+PostfixExpressionCalculator(ls));
System.out.println("前缀表达式2: "+prefixExpressionCalculator(ls2));
System.out.println("test3: "+PostfixExpressionCalculator(Infix2PostfixExpression(test3)));
}
}
输出结果: 文章来源地址https://www.toymoban.com/news/detail-751526.html
文章来源地址https://www.toymoban.com/news/detail-751526.html
到了这里,关于数据结构——前缀、中缀、后缀表达式实现和转换(Java)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!