前言
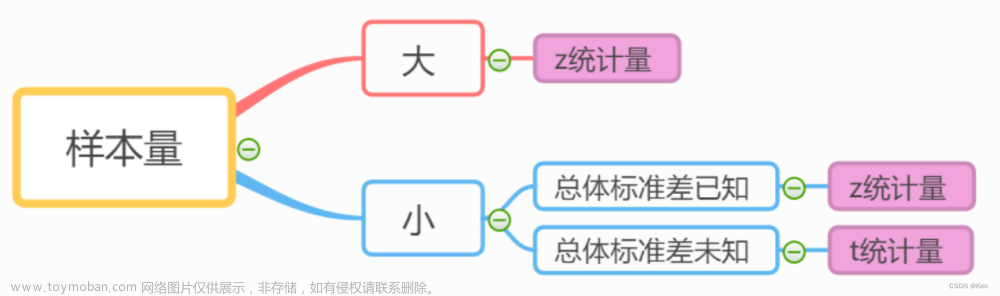
1. 不同检验方法最小样本量的确认
由统计量反推得到

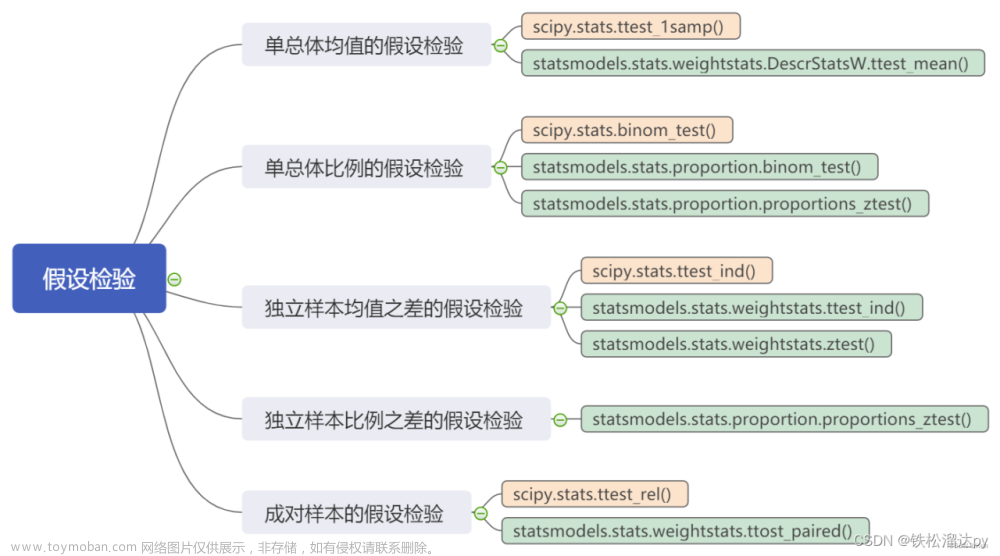
2. 检验方法
- 方差齐性检验(F检验):两个独立样本的方差差异检验,反映了平均值的代表性。方差齐次检验前提要近似正态分布。
- 正态性检验:是否符合正态分布
- 似然比检验:比较样本不同似然函数,检验其分布
参数检验基于共同的两个假设:正态性假定,方差齐性假定
一、方差齐性检验
方差齐性指不同组间的总体方差是一样的。而方差分析的前提是要组间的总体方差保持一致。先想想方差分析是做什么呢?方差分析是用来比较多组之间均值是否存在显著差异。那如果方差不一致,也就意味着值的波动程度是不一样的,如果此时均值之间存在显著差异,不能够说明一定是不同组间处理带来的,有可能是大方差带来大的波动;如果方差一样,也就意味着值的波动程度是一样的,在相同波动程度下,直接去比较均值,如果均值之间存在显著差异,那么可以认为是不同组间处理带来的。
1.1 方差比
两组方差的比,用较大一组的方差除较小一组的方差,最后得到一个F值,然后根据F值的大小来判断两组之间的方差是否相等。F值越大,则认为两组方差越不相等。
1.2 Hartley检验
Hartley检验与方差比的思想比较类似,差别在于Hartley检验用于多组方差的检验,用多组中最大的方差除最小的方差,得到一个F值,然后通过F值的判断来对方差齐性进行判断。
1.3 Levene检验
Levene检验是将每个值先转换为为该值与其组内均值的偏离程度,然后再用转换后的偏离程度去做方差分析,即组间方差/组内方差, F检验。
1.4 BF法
Levene检验最开始计算组内均值的时候只是用了组内平均数, BF法添加了中位数和截取均值的方法
1.5 Bartlett检验
Bartlett检验的核心思想是通过求取不同组之间的卡方统计量,然后根据卡方统计量的值来判断组间方差是否相等。该方法极度依赖于数据是正态分布,如果数据非正态分布,则的出来的结果偏差很大。
二、似然比检验
似然比检验的原假设H0是:θ=θ0,备择假设H1:θ=θ1,其中θ0是θ1的子集。

似然比表示θ取不同值对应的似然函数的比值。如果λ很大,说明参数θ=θ1时对应的似然性要比θ=θ0时对应的似然性大。此时,更倾向于拒绝H0假设;反之,若此值较小,说明参数θ=θ0时对应的似然性要比θ=θ1时对应的似然性大,更倾向于接受H0假设。
那λ到底大于多少算大,小于多少算小呢?这个时候就需要有个临界值λ0,如果λ>λ0,那么就拒绝H0假设。
接下来的问题就是求取λ0,要临界值λ0,必须知道当H0成立时λ的分布,当n足够大时,λ是服从卡方分布的,知道分布,然后再根据显著性水平α就可以计算出临界值了。
三、异常值检验
1. Q检验
Q检验又称舍弃商法,主要是用来对可疑值(异常值)进行取舍判断的。
Q检验的核心思想其实和t检验的核心思想是一致的,都是用来检验不同的观测值之间是否有显著差异,即是否来自于同一总体,如果差异不显著,则说明是来自于同一总体,否则就不是。
- step1:将所有观测数据按照从小到大的顺序进行排列
- step2:求最大值与最小值之间的差值,称为极差
- step3:计算想删除值与其相邻值之间差值的绝对值
- step4:用step3算出来的值除step2算出的值,该值就是q统计量
- step5:根据观测值个数以及置信水平,查q值表
- step6:比较q统计量与q值表中查出的结果,如果q统计量小于q值表查出来的结果,则不应该删除,否则就可以删除
Q检验除了被用在要不要剔除异常值以外,还主要用在多重比较中,比如有多个组别,需要判断各个组别两两之间的差异程度时也会用到。或者时间序列的白噪声检验
多重比较法的一种:LSD(最小显著差异方法,least significant difference)
具体步骤:
1.提出假设:H0:两组之间无差异;H1:两组之间有差异。
2.计算检验统计量:两组均值之差的绝对值。
3.计算LSD,公式为:
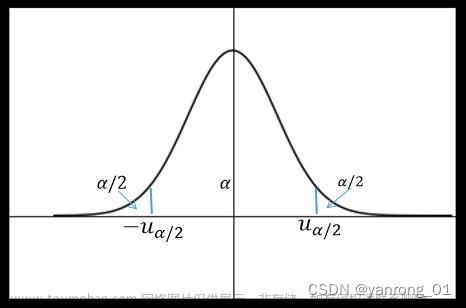
tα/2为t分布的临界值,通过查t分布表得到,其自由度为n-k,n为样本总数,k为因素中不同水平的水平个数;MSE为组内方差;ni和nj分别为第i个样本和j个样本的样本量。
4.根据显著性水平α做作出决策,如果均值之差的绝对值大于LSD,则拒绝H0,否则不拒绝H0。
2. Grubbs' Test
Grubbs检验用于检测单变量数据集中的单个异常值,该单变量数据集遵循近似正态分布。
如果怀疑可能存在多个异常值,建议使用Tietjen-Moore检验或广义极端学生化偏差检验而不是Grubbs检验。(Grubbs必须反复执行以筛选多个离群值)
Grubbs检验也称为最大标准残差检验。实际上,Grubbs' Test可理解为检验最大值、最小值偏离均值的程度是否为异常。
H0:数据集中没有异常值
H1:数据集中只有一个异常值
四、正态性检验
对于正态性检验,建议首先利用直方图或核密度估计得到样本数据的分布图,若分布严重偏态或尖峰,可认为其不是来自于正态分布;若根据直方图或核密估计分布不容易做出判断,再利用各检验方法对其检验。
SPSS 规定:当样本含量 3≤n≤5000 时,结果以 Shapiro—Wilk(W 检验) 为准,当样本含量 n>5000 结果以 Kolmogorm —Smimov(D 检验,修正后的KS检验,即Lillie检验,见2.2.3) 为准。
SAS 规定:当样本含量 n≤2000 时,结果以 Shapim—Wilk(W 检验) 为准,当样本含量 n>2000 时,结果以 Kolmogorov—Smimov(D 检验,修正后的KS检验) 为准。
1. 描述统计方法
- Q-Q图:x轴为分位数,y轴为分位数对应的样本值
- P-P图:QQ图y轴是具体的分位数对应的样本值,而P-P图是累计概率
- 直方图
- 茎叶图
#QQ图
from scipy import stats
stats.probplot(x, dist="norm", plot=plt)
#R语言 -QQ图
library(car)
qqnorm(x)2. 统计检验方法
2.1 SW检验
S就是偏度(Skewness),W就是峰度(Kurtosis)

偏度用来描述数据分布的对称性,正态分布的偏度为0。计算数据样本的偏度,当偏度<0时,称为负偏,数据出现左侧长尾;当偏度>0时,称为正偏,数据出现右侧长尾;当偏度为0时,表示数据相对均匀的分布在平均值两侧,不一定是绝对的对称分布,此时要与正态分布偏度为0的情况进行区分。当偏度绝对值过大时,长尾的一侧出现极端值的可能性较高。
峰度用来描述数据分布陡峭或是平滑的情况。正态分布的峰度为3,峰度越大,代表分布越陡峭,尾部越厚;峰度越小,分布越平滑。很多情况下,为方便计算,将峰度值-3,因此正态分布的峰度变为0,方便比较。在方差相同的情况下,峰度越大,存在极端值的可能性越高。
s = pd.Series(data)
print(s.skew()) #偏度计算
print(s.kurt()) #峰度计算2.2 Kolmogorov-Smirnor检验(KS检验)
KS检验是基于样本累积分布函数来进行判断的。可以用于判断某个样本集是否符合某个已知分布,也可以用于检验两个样本之间的显著性差异。
如果是判断某个样本是否符合某个已知分布,比如正态分布,则需要先计算出标准正态分布的累计分布函数,然后在计算样本集的累计分布函数。两个函数之间在不同的取值处会有不同的差值。我们只需要找出来差值最大的那个点D。然后基于样本集的样本数和显著性水平找到差值边界值(类似于t检验的边界值)。判断边界值和D的关系,如果D小于边界值,则可以认为样本的分布符合已知分布,否则不可以。
Dn=max(累计频率−理论分布)
D值越小越接近正态分布
#Python
from scipy import stats
stats.kstest(x, 'norm', (x.mean(), x.std()))
#R
ks.test(x, "pnorm",mean(x),sd(x))
#x为要检验的样本数据,其函数默认修改的精确公式、双边检验。
#需要大样本近似命令中加exact = F;
#单边我们可以用alternative = "less"或alternative= "greater"选择。
2.3 Anderson-Darling检验(AD检验)
AD检验是在KS基础上进行改造的,KS检验只考虑了两个分布之间差值最大的那个点,但是这容易受异常值的影响。AD检验考虑了分布上每个点处的差值。
2.4 Shapiro-Wilk检验(W检验)
W检验(Shapiro-Wilk的简称)是基于两个分布的相关性来进行判断,会得出一个类似于皮尔逊相关系数的值。值越大接近1,说明两个分布越相关,越符合某个分布。

原假设正态性, 当p值小于某个显著性水平,则认为不是正态分布
#python
from scipy import stats
stats.shapiro(x)
#R
shapiro.test(x)2.5 Jarque-Bera (JB)检验(时间序列中常用)
JB检验线性回归模型的残差是否符合正态分布。
原假设H0:模型残差e服从正态分布
Prob(JB)<0.05:显著=>拒绝原假设H0=>模型残差e不服从正态分布
Prob(JB)>0.05:不显著=>不能拒绝原假设H0=>模型残差e服从正态分布
import scipy.stats as ss
ss.jarque_bera(y)五、一致性检验

1. Kappa一致性检验
检验条件:行和列均反应同一事物某一属性的相同水平
检验目的:检验两种角度对同一事物的判断是否一致
Kappa一致性检验样本为两变量多分类,Kendall’s W 检验样本为多列有序变量
from sklearn.metrics import cohen_kappa_score2. Kendall’s W 检验
检验目的:检验3个及以上角度对同一事物判断是否一致
检验条件:
- 1)观察者不少于3人,判定结果是连续变量或有序分类变量。
- 2)不同观测者判定的对象相同;
- 3)观察者之间相互独立。
W系数:Kendall cofficient of concordance
代码例子:
| 教师评级 | 一 | 二 | 三 | 四 | 五 | 六 |
|---|---|---|---|---|---|---|
| A | 3 | 1 | 2 | 5 | 4 | 6 |
| B | 2 | 1 | 3 | 4 | 5 | 6 |
| C | 3 | 2 | 1 | 5 | 4 | 6 |
| D | 4 | 1 | 2 | 6 | 3 | 5 |
| E | 3 | 1 | 2 | 6 | 4 | 5 |
| F | 4 | 2 | 1 | 5 | 3 | 6 |
import numpy as np
from collections import Counter
def getT(A):
T = []
for a in A:
C = Counter(a)
E = list(C.keys())
F = list(C.values())
G = np.arange(0, len(E))
u = 0
for b in G:
if(F[b] > 1):
u += (F[b]**3 - F[b])
T.append(u)
return np.array(T)
A = np.array([[3, 1, 2, 5, 4, 6],
[2, 1, 3, 4, 5, 6],
[3, 2, 1, 5, 4, 6],
[4, 1, 2, 6, 3, 5],
[3, 1, 2, 6, 4, 5],
[4, 2, 1, 5, 3, 6]]);
k = len(A)
n = len(A[0])
R = A.sum(axis=0)
S = np.square(R).sum() - np.square(R.sum()) / n
T = getT(A)
W = 12 * S / (np.square(k) * (n**3 - n) - k * T.sum())
print(W)
六、相关性检验
1. KMO(Kaiser-Meyer-Olkin) 检验
比较变量间简单相关系数和偏相关系数的指标。如果原始数据中确实存在公共因子,则各变量之间的偏相关系数应该很小,这时,KMO的值接近于1,因此,原数据适用于因子分析
2. Bartlett 球度检验
H0:相关系数矩阵是单位矩阵(变量不相关)
H1:相关系数矩阵不是单位矩阵(变量相关)
巴特利特球度检验的统计量是根据相关系数矩阵的行列式得到的,如果显著性水平小于给定的α,那么应该拒绝零假设,即原始变量之间存在相关性,适合于做主成份分析;相反,不宜于做主成分分析。
3. Kendall Ranking Correlation(肯德尔Ranking相关系数)
from scipy.stats import kendalltau七、独立性检验
1. 皮尔逊卡方检验 Pearson's chi-squared test
广泛应用于分类变量(categorical data)的独立性检验中,也可用于分类变量的比较检验中。这两种检验都需要用到R×C列联表(R×C contingency table),其中R表示行(Row),C表示列(Column)。本文只讨论行列变量都是无序变量的情形,最简单的情形是行与列都是二分类无序变量,这样的数据也称为四格表资料。
一文详解卡方检验 - 知乎
八. 参数检验
- 单样本t检验
- 两样本t检验 (方差齐性使用levene检验)
- 配对样本t检验
- 方差分析(Anasis Of Variance, ANOVA)
九. 非参数检验
- Mann-Whitney U Test (曼惠特尼U检验)
- Wilcoxon Signed-Rank Test
- Kruskal-Wallis H Test (K-W检验)
- Friedman Test (弗里德曼检验)
- Kolmogorv-Smirnov Test (K-S检验)
十. 时间序列平稳性检验
- Augmented Dickey-Fuller Unit Root Test (单位根检验)
- Kwiatkowski-Phillips-Schmidt-Shin Test
十一. 时空交互检验
Knox时空交互模型:Knox法是一种全局时空聚集探测方法[30]。它首先人为设定空间阈值s和时间阈值t,将所有事件点两两配对,并计算空间距离sij和时间距离tij。当sij≤s时,认为事件点空间邻近;当tij≤t时,认为事件点时间邻近。根据事件是否时空邻近,对不同类别的事件对数进行计数,其中时空邻近事件对数即为Knox指数,假设检验采用χ2检验。
基于时空密度的聚类方法:时空扫描统计需要预先假定数据的概率分布模型,且结果受扫描窗口的影响较大,不能详细描述时空簇的位置和形状信息[38]。为了克服这些问题,近年来,越来越多基于时空密度的聚类方法被提出。时空密度聚类是空间密度聚类在时空域上的扩展,采用密度作为实体间相似性的度量标准,将时空簇看作一系列被低密度区域(噪声)分割的高密度连通区域[39],其中最常用的方法是ST-DBSCAN。
ST-DBSCAN法由DBSCAN增加时间维度扩展而来,其假设i和j为直接密度可达的两个核心点,如果两个核心点的邻域的非空间属性平均距离小于阈值,则对这两个邻域进行聚类[40]。ST-DBSCAN不需要预先假设数据的分布模型,且可以检测任意形状的聚集簇。目前该法多应用于道路交通领域,在疾病聚集方面的应用尚处于起步阶段。Guo等[41]采用ST-DBSCAN对2005-2011年中国狂犬病病例进行分析,共检测到480个聚类。该法存在的不足是需要设定空间、时间、非空间距离阈值和密度阈值,DBSCAN对用户定义的参数很敏感,因此如何选取合适的参数十分关键。很多研究对此提出解决对策,如基于窗口最近邻法[42]、自适应法[43]等确定阈值。基于时空密度的聚类方法是目前研究的热点,新方法不断提出,如时空不规则聚类法[44]、时空有序点识别聚类结构[45]、Bregman Block共聚类算法[46]等。
疾病时空聚集分析的研究与进展
Knox时空交互检验空间阈值确定方法
References
https://blog.csdn.net/junhongzhang/category_11501188.html
最小样本量n的选择 - 知乎
正态性检验方法汇总_米竹的博客-CSDN博客_正态性检验文章来源:https://www.toymoban.com/news/detail-751569.html
Python代码
基于Python的19种假设检验实现 - 知乎文章来源地址https://www.toymoban.com/news/detail-751569.html
到了这里,关于【统计】假设检验方法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!