题目链接：leetcode不同路径
目录
题目解析：
算法原理
1.状态表示
2.状态转移方程
3.初始化
4.填表顺序
5.返回值
编写代码
题目解析：
题目让我们求总共有多少条不同的路径可到达右下角；
由题可得：
机器人位于一个 m x n 网格；
机器人每次只能向下或者向右移动一步；
我们拿示例2来分析：
则根据题目要求我们只能向下或者向右移动一步，不能向上或向左回退；
所以这里我们一共有三种走法：
算法原理:
1.状态表示
根据题目要求，先创建一个 m x n 大小的dp表
首先先思考dp表里面的值所表示的含义（是什么？）
dp[i][j]表示到达i*j时一共有多少种方式；
这种状态表示怎么来的？
1.经验+题目要求
经验：以i*j位置为结尾，
题目让我们求到达右下角有多少种方式，那么这里我们可以dp[i][j]来表示。
所以这里我们用i*j表示右下角位置；
2.状态转移方程
dp[i][j]等于什么？
用之前或者之后的状态，推导出dp[i][j]的值；
根据最近的最近的一步，来划分问题
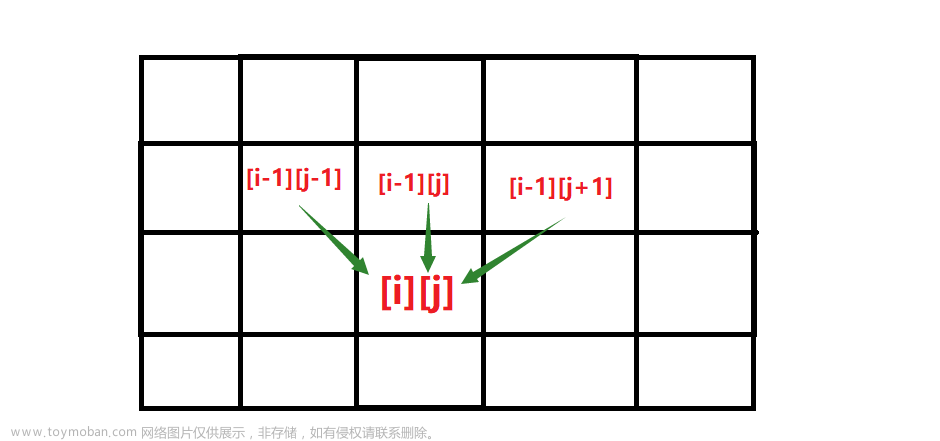
当机器人到达dp[i-1][j]时，我们知道它到达[i-1][j]有dp[i-1][j]方式，
此时只需要从[i-1][j]往下走一步就可以到达目标位置，即：
……-->[i-1][j]-->(往下走一步)[i][j]；
……-->[i-1][j]-->(往下走一步)[i][j]；
……-->[i-1][j]-->(往下走一步)[i][j]；
……
所以往下走一步就可以到达目标位置的方式就有dp[i-1][j]种；
那么同理，
当机器人到达dp[i][j-1]时，我们知道它到达[i][j-1]有dp[i][j-1]方式，
此时只需要在到达[i][j-1]方式的后面往右边走一步就可以到达目标位置，即：
……-->[i][j-1]-->(往右边走一步)[i][j]；
……-->[i][j-1]-->(往右边走一步)[i][j]；
……-->[i][j-1]-->(往右边走一步)[i][j]；
……
所以往右边走一步就可以到达目标位置的方式就有dp[i-1][j]种；
综上所述，我们只要将到达[i][j-1]与[i-1][j]的总方法相加即可得到，到达[i][j]位置的总方法，
即：
dp[i][j]=dp[i-1][j]+dp[i][j-1];
3.初始化
(保证填表的时候不越界)
由我们的状态转移方程得：
在0行0列的时候越界，所以我们这里可以在m*n的外围多加1行1列，如图：
还有一个问题是：
我们要拿新增用来初始化的行和列要初始化为几呢？
假设：如果所需要到达的位置就在机器人所在的位置，此时有一种方式；
根据状态转移方程，在[0][1]与[1][0]位置要有一个位置需要初始化为1，其他位置初始化为0
我们这里选择[0][1]初始化为1
4.填表顺序
（为了填写当前状态的时候，所需要的状态已经计算过了）
这里所需要的状态是：到达该位置的上面和左边位置的方式
所以填表顺序：
从上到下填写每一行
从左到右填写每一列
5.返回值
（根据题目要求和状态表示）
综上分析：
返回值为：dp[m][n];文章来源：https://www.toymoban.com/news/detail-751638.html
编写代码:
文章来源地址https://www.toymoban.com/news/detail-751638.html
class Solution {
public:
int uniquePaths(int m, int n) {
//1.创建dp表
//2.初始化
//3.填表
//4.返回结果
vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
dp[0][1]=1;
for(int i=1;i<m+1;i++)
for(int j=1;j<n+1;j++)
dp[i][j]=dp[i][j-1]+dp[i-1][j];
return dp[m][n];
}
};到了这里，关于【动态规划】路径问题_不同路径_C++的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
