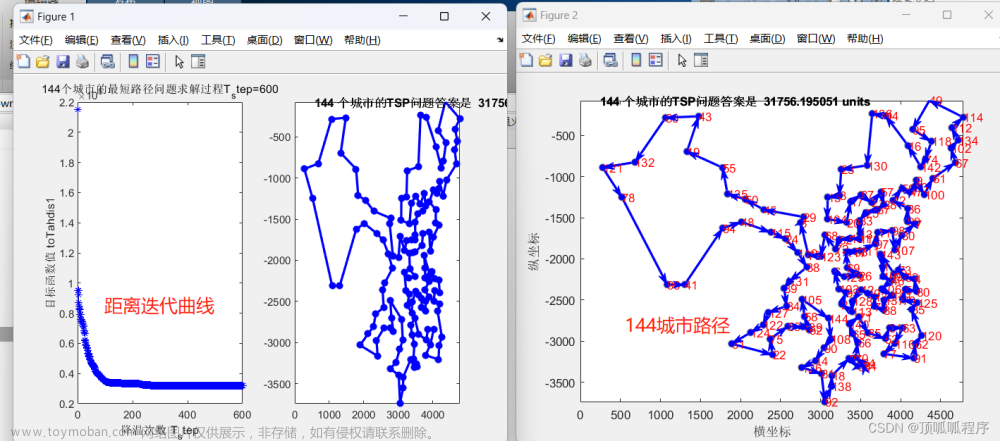
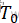模拟退火算法概述
>模拟退火算法（Simulated Annealing，简称SA）的思想最早是由Metropolis等提出的。其出发点是基于物理中固体物质的退火过程与一般的组合优化问题之间的相似性。模拟退火算法是一种通用的优化算法，其物理退火过程由以下三部分组成：
>加温过程。其目的是增强粒子的热运动，使其偏离平衡位置。当温度足够高时，固体将熔为液体，从而消除系统原先存在的非均匀状态。
>等温过程。对于与周围环境交换热量而温度不变的封闭系统，系统状态的自发变化总是朝自由能减少的方向进行的，当自由能达到最小时，系统达到平衡状态。
>冷却过程。使粒子热运动减弱，系统能量下降，得到晶体结构。
>加温过程对算法设定初温，等温过程对应算法的Metropolis抽样过程，冷却过程对应控制参数的下降。这里能量的变化就是目标函数，我们得到的最优解就是能量最低态。其中Metropolis准则是SA算法收敛于全局最优解的关键所在，Metropolis准则以一定的概率接受恶化解，这样就使算法跳离局部最优的陷阱。
模拟退火算法在优化问题的时候，采用的就是类似于物理退火让固体内部粒子收敛到一个能量最低状态的过程，实现算法最终收敛到最优解的目的。
物理退火过程和模拟退火算法的基本概念对照表
| 物理退火过程 | 模拟退火算法 |
| 物体内部的状态 | 问题的解空间(所有可行解） |
| 状态的能量 | 解的质量(适应度函数值) |
| 温度 | 控制参数 |
| 熔解过程 | 设定初始温度 |
| 温水冷却过程 | 控制参数的修改(温度参数的下降) |
| 状态的转移 | 解在领域中的变化 |
| 能量最低状态 | 最优解 |
Metropolis准则
Metropolis准则定义了物体在某一温度 T 下从状态 i 转移到状态 j 的概率
,如公式所示，
其中e为自然对数，E(i)和E(j)分别表示固体在状态i和状态j下的内能，
,表示内能的增量，K是玻尔兹曼常数。
在某个温度T下，系统处于某种状态，由于粒子的运动，系统的状态会发生变化，并且导致系统能量的变化。如果变化是朝着减少系统能量的方向进行的，那么就接受该变化，否则以一定的概率接受这种变化。另一方面，从
模拟退火算法流程
1. 初始化：取初始温度T0足够大，令T = T0，任取初始解S1。
2. 对当前温度T，重复第 (3) ~ (6) 步。
3. 对当前解S1随机扰动产生一个新解S2。
4. 计算S2的增量 df = f(S2) - f(S1)，其中 f(S1) 为 S1 的代价函数。
5. 若df < 0，则接受S2作为新的当前解，即S1 = S2; 否则计算S2的接受概率exp(-df/T)，即随机产生(0,1)区间上均匀分布的随机数rand，若exp(-df/T) > rand，也接受S2作为新的当前解S1 = S2，否则保留当前解S1。
6. 如果满足终止条件Stop，则输出当前解S1为最优解，结束程序，终止条件Stop通常取为在连续若干个Metropolis链中新解S2都没有被接受时终止算法或者是设定结束温度；否则按衰减函数衰减T后返回第(2)步。
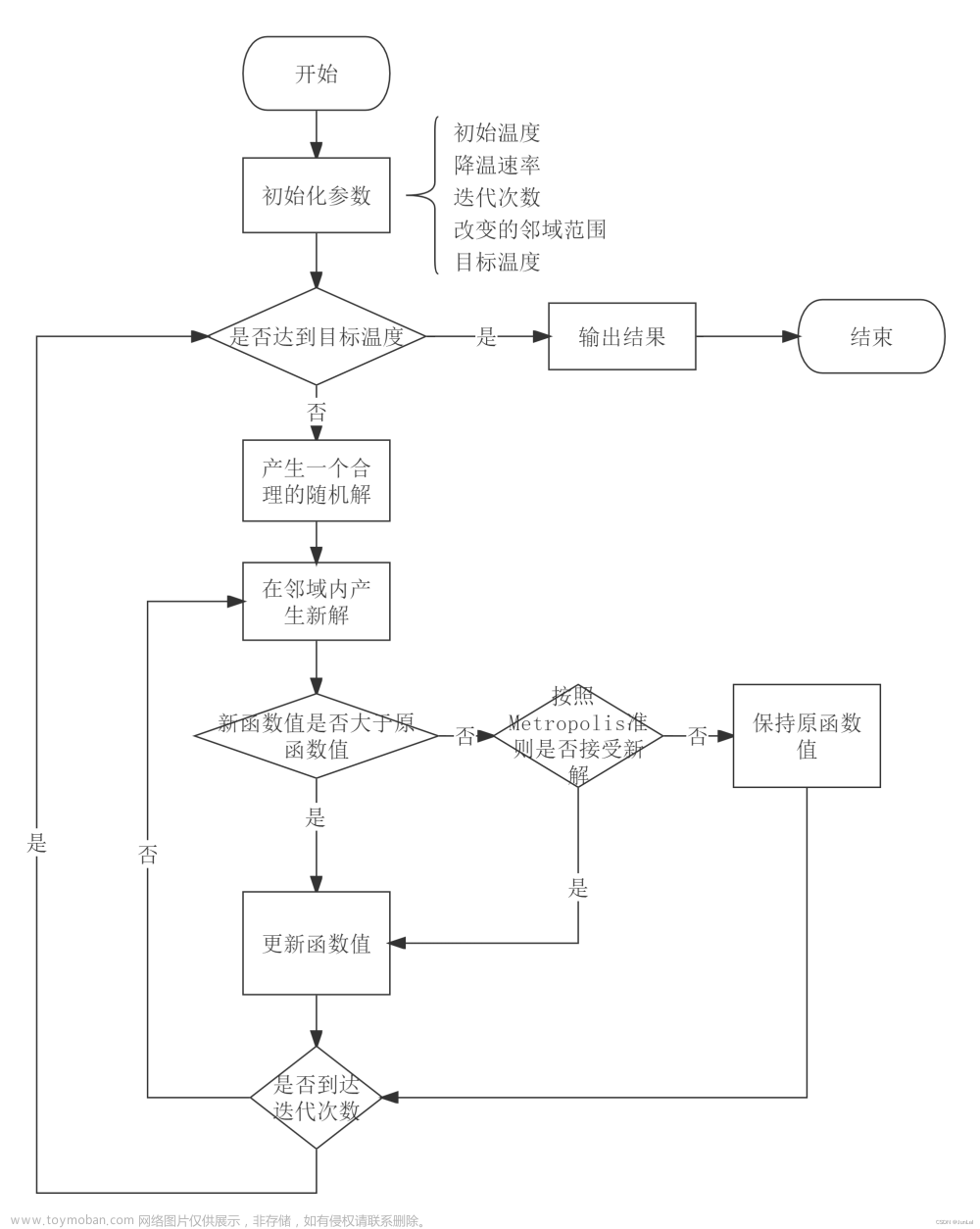
模拟退火算法在求解最优化问题的时候，算法的基本流程图和伪代码如图所示：
从流程图中可以看到模拟退火具有两层循环，内循坏模拟的是在给定的温度下系统达到热平衡的过程。在该循环中，每次都从当前解 i 的领域中随机找出一个新解 j，然后按照Metropolis准则概率地接受新解。算法中的random(0,1)是指在区间[0,1]上按均匀分布产生一个随机数，而所谓的内层达到热平衡也是一个笼统的说法，可以定义为循环一定的代数，或者基于接受率定义平衡等。算法的外层循环是一个降温的过程，当在一个温度下达到平衡后，开始外层的降温，然后在新的温度下重新开始内循环。降温的方法可以根据具体问题具体设计，而且算法流程图中给出的初始温度T也需要算法的使用者根据具体的问题而制定。
模拟退火算法在求解最优化问题的时候，涉及以下几个方面的基本要素。
1.初始温度
初始温度
的设置是影响模拟退火算法全局搜索性能的重要因素之一。实验表明，初温越大，获得高质量解的几率越大，但花费的计算时间将越多。因此，初温的确定应折中考虑优化质量和优化效率，常用方法包括以下几种。
>均匀抽样一组状态，以各状态目标值的方差为初温；
>随机产生一组状态，确定两两状态间的最大目标值差
，然后依据差值，利用一定的函数确定初温。例如，
，其中
为初始接受概率；
>利用经验公式给出初始温度。
2.领域函数
领域函数(状态产生函数)应尽可能保证产生的候选解遍布全部解空间，通常由两部分组成，即产生候选解的方式和候选解产生的概率分布。候选解一般采用按照某一概率密度函数对解空间进行随机采样来获得。概率分布可以是均匀分布、正态分布、指数分布等。
3.接受概率
指从一个状态
(一个可行解）向另一个状态
(另一个可行解)的转移概率，通俗的理解是接受一个新解为当前解的概率。它与当前的温度参数
有关，随温度下降而减少，一般采用Metropolis准则。
4.冷却控制
指从某一较高温状态
而快速模拟退火算法的降温方式为：
这两种方式都能够使得模拟退火算法收敛于全局最小点。
5.内层平衡
内层平衡也称Metropolis抽样稳定准则，用于决定在各温度下产生候选解的数目。
常用的抽样稳定准则包括以下几项。
>检验目标函数的均值是否稳定；
>连续若干步的目标值变化较小；
>预先设定的抽样数目，内循环代数。
6.终止条件
算法终止准则，常用的包括以下几项。
>设置终止温度的阈值;
>设置外循环迭代次数;
>算法搜索到的最优值连续若干步保持不变；
>检验系统熵是否稳定。
模拟退火算法的特点
>与遗传算法、粒子群优化算法和蚁群算法等不同，模拟退火算法不属于群优化算法，不需要初始化种群操作。
>收敛速度较慢。
>温度管理、退火速度等对寻优结果均有影响。
模拟退火算法代码示例
以下是一个简单的模拟退火算法的 Python 代码示例：
import math
import random
# 目标函数
def obj_func(x, y):
return math.sin(x) + math.cos(y)
# 初始温度
init_temp = 1000.0
# 终止温度
end_temp = 1e-8
# 冷却速率
cool_rate = 0.99
# 初始解
x = random.uniform(-10, 10)
y = random.uniform(-10, 10)
# 当前温度
cur_temp = init_temp
# 主循环
while cur_temp > end_temp:
# 随机生成新解
new_x = x + random.uniform(-1, 1)
new_y = y + random.uniform(-1, 1)
# 计算新解的目标函数值
new_obj = obj_func(new_x, new_y)
# 计算能量差
delta_e = new_obj - obj_func(x, y)
# 判断是否接受新解
if delta_e < 0 or math.exp(-delta_e / cur_temp) > random.random():
x, y = new_x, new_y
# 降温
cur_temp *= cool_rate
# 输出最终解
print("x =", x, "y =", y, "obj =", obj_func(x, y))在该示例代码中，
obj_func函数表示目标函数，init_temp表示初始温度，end_temp表示终止温度，cool_rate表示冷却速率，x和y表示当前解，cur_temp表示当前温度。在主循环中，每次随机生成一个新解，计算能量差，然后根据一定的概率接受新解或保持原解。在接受新解时，更新当前解，否则保持原解不变。随着温度的不断降低，算法逐渐收敛到全局最优解。文章来源：https://www.toymoban.com/news/detail-751791.html
参考文献：计算智能 张军文章来源地址https://www.toymoban.com/news/detail-751791.html
到了这里，关于智能优化算法学习笔记（2）–模拟退火算法（SA）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
