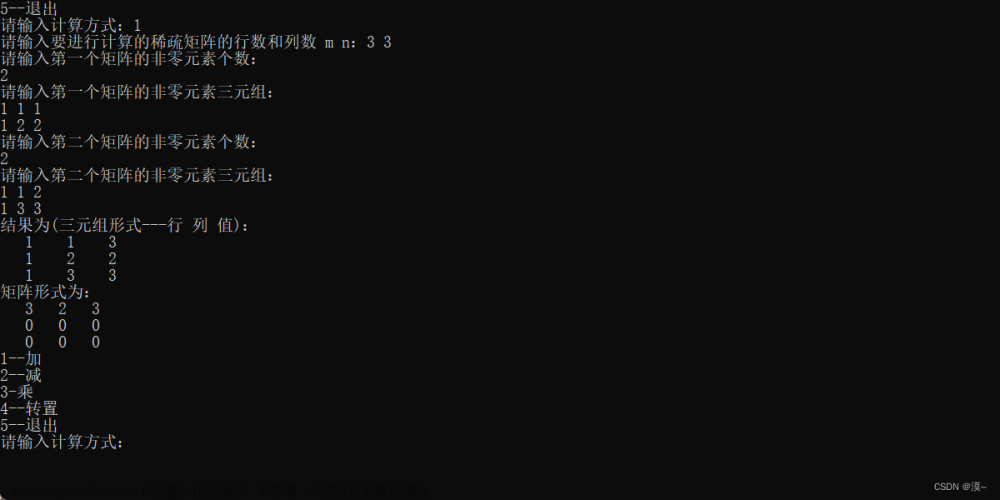
一、十字链表
typedef struct OLNode {
int i, j; // 该非零元的行和列下标
ElemType e;
struct OLNode *right, *down; // 该非零元所在行表和列表的后继链域
}OLNode, *OLink;
typedef struct {
OLink *rhead, *chead; // 行和列链表头指针向量基址由CreateSMatrix分配
int mu, nu, tu; // 稀疏矩阵的行数、列数和非零元个数
}CrossList;
二、三元组顺序表
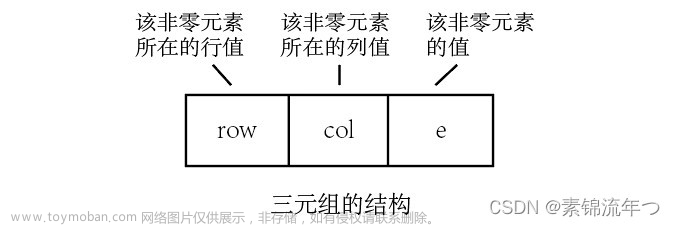
1. 三元组顺序表数据结构
#define MAXSIZE 12500 // 假设非零元个数的最大值为12500
typedef struct {
int i, j;
ElemType e;
}Triple;
typedef struct {
Triple data[MAXSIZE + 1]; // 非零元三元组表，data[0]未用
int mu, nu, tu; // 矩阵的行数、列数和非零元个数
}TSMatrix;
注意：data[]中的元素是按行存储或者按列存储的，所以在将三元组逆置时，不能简单地将行列下标对换，data[]数组中元素的顺序也需要重新排列
2. 三元组表示稀疏矩阵转置算法1
// 时间复杂度为O(nu*tu)
void transpose1(TSMatrix M, TSMatrix &T) {
T.mu = M.nu; T.nu = M.mu; T.tu = M.tu;
int q = 1;
// 按照矩阵M的列序进行转置
for (int col = 1; col <= M.nu; ++col) {
// 为了找到M的每一列中的所有非零元素，需要对其三元组表从第一行起整个扫描一遍
for (int p = 1; p <= M.tu; ++p) {
if (M.data[p].j == col) {
T.data[q].i = M.data[p].j;
T.data[q].j = M.data[p].i;
T.data[q].e = M.data[p].e;
++q;
}
}
}
}
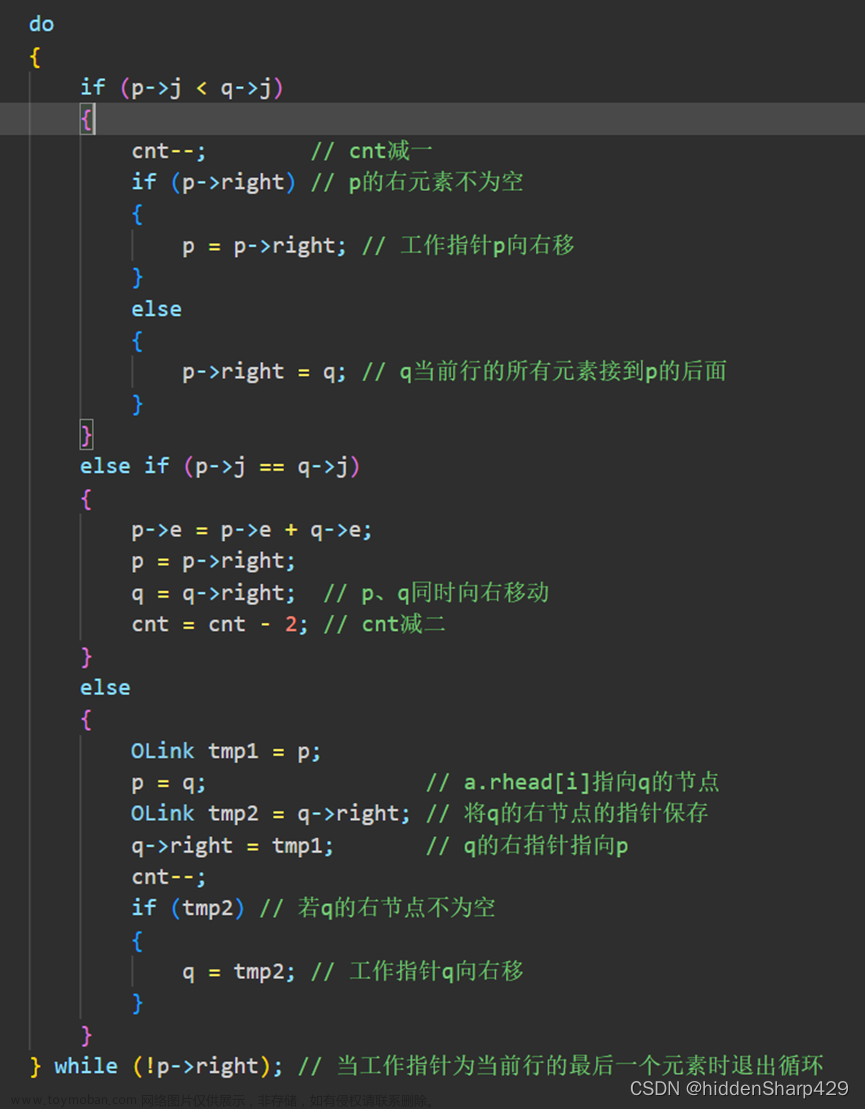
3. 三元组表示稀疏矩阵转置算法2：快速转置
// 快速转置
// 时间复杂度
void transpose1(TSMatrix M, TSMatrix &T) {
T.mu = M.nu; T.nu = M.mu; T.tu = M.tu;
// 求M中每一列含非零元个数
int num[M.nu + 1] = {0};
for (int t = 1; t <= M.tu; ++t) {
++num[M.data[t].j];
}
// 求第col列中第一个非零元在T.data中的序号
int cpot[M.nu + 1];
cpot[1] = 1;
for (col = 2; col <= M.nu; ++col) {
cpot[col] = cpot[col - 1] + num[col - 1];
}
for (int p = 1; p <= M.tu; ++p) {
int col = M.data[p].j;
int q = cpot[col];
T.data[q].i = M.data[p].j;
T.data[q].j = M.data[p].i;
T.data[q].e = M.data[p].e;
++cpot[col];
}
}
三、行逻辑链接的顺序表
为了便于随机存取任意一行的非零元，则需知道每一行的第一个非零元在三元组表中的位置。为此，可将上节快速转置矩阵的算法中创建的，指示“行“信息的辅助数组 cpot 固定在稀疏矩阵的存储结构中。称这种“带行链接信息”的三元组表为行逻辑链接的顺序表，其类型描述如下：文章来源：https://www.toymoban.com/news/detail-752339.html
typedef struct {
Triple data[MAXSIZE + 1]; // 非零元三元组表
int rpos[MAXRC + 1]; // 各行第一个非零元的位置表
int mu, nu, tu; // 矩阵的行数、列数和非零元个数
}RLSMatrix;
文章来源地址https://www.toymoban.com/news/detail-752339.html
到了这里，关于【数据结构】稀疏矩阵存储的三种方法及三元组表示稀疏矩阵转置算法的两种实现 —— C++的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
![[数据结构(C语言版本)上机实验]稀疏矩阵的三元组顺序表压缩存储以及转置实现(含快速转置）](https://imgs.yssmx.com/Uploads/2024/02/435123-1.png)
