构造无向图，进行深度优先遍历和广度优先遍历-Toy模板网

这篇具有很好参考价值的文章主要介绍了构造无向图，进行深度优先遍历和广度优先遍历。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一. 实验要求
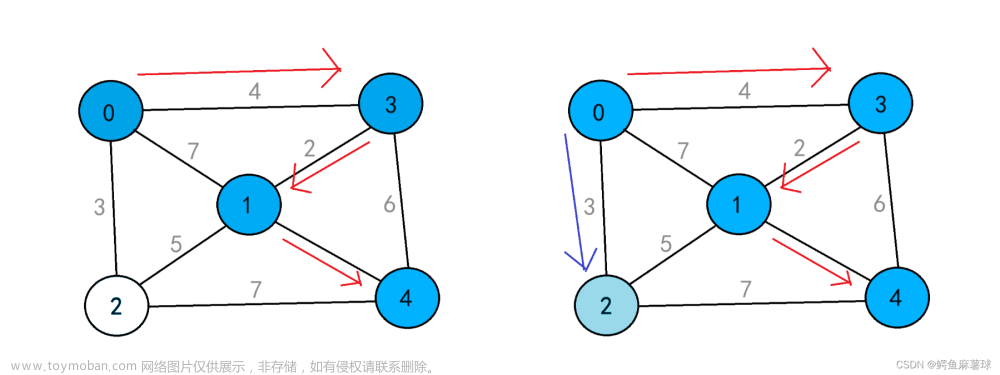
实现利用邻接矩阵构造无向图的算法，在此基础上进行深度优先遍历和广度优先遍历。
二. 实验目的
通过该实验，使学生掌握图的几种存储结构，理解图的深度优先和广度优先遍历算法的思想和实现办法
三、设计思想
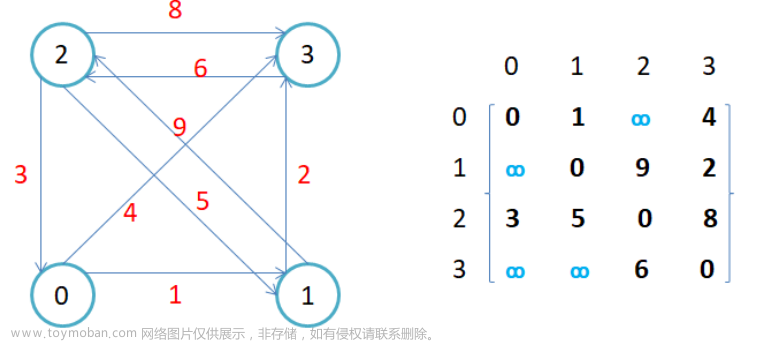
1.创建网图。网图是利用邻接矩阵来存储的。先从键盘输入图的顶点树vex和边数arc。创建一个正方形矩阵，边数等于vex。然后输入这vex个顶点的符号。再输入图中i个顶点和j个顶点相连，使矩阵中的第i行第j列和第j行第i列的值为1，表示两个顶点i和j相通，矩阵中其他元素的值为0，表示这两个顶点之间无线。
2.输出邻接矩阵。根据创建网图中创建的邻接矩阵，利用for循环来控制输出邻接矩阵即可。
3.深度优先遍历。从第一个顶点1开始遍历。先输出1。借用辅助数组vis，以便判断顶点是否已经遍历过，已被遍历过的元素为true，没有遍历过的为false。利用for循环，如果矩阵中第vex行的第i个是0或是已被调用过的顶点，则continue一次for循环；否则，继续深度遍历这个未被调用过的第i个顶点。
4.广度优先遍历。构建一个置空的辅助队列que，借助辅助数组vis，以便判断顶点是否已经遍历过。将第一个顶点vex入队，vis[vex]=true。当队列que不为空时，进行while循环：将队列que的队头元素输出，并利用for循环寻找邻接矩阵中第vex行是否有未被访问过的顶点，如果有，则入队，并且辅助数组vis中的值改为true。

三. 主要源代码

#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <algorithm>
#define N 100
using namespace std;

bool vis[N];
struct Graph{
	int vex[N];
	int graph[N][N];
	int sum_vex, sum_arc;
};
void print();
void init(Graph &g) {
	for (int i = 1; i <= g.sum_vex; ++i) {
		for (int j = 1; j <= g.sum_vex; ++j) {
			g.graph[i][j] = 0;
		}
	}
	return;
}
void creat(Graph &g) {
	cout << "请输入顶点数和边数：";
	cin >> g.sum_vex >> g.sum_arc;
	cout << endl;
	init(g);
	cout << "请输入" << g.sum_vex << "个顶点：";
	for (int i = 1; i <= g.sum_vex; ++i) {
		cin >> g.vex[i];
	}
	sort(g.vex + 1, g.vex + g.sum_vex + 1);
	cout << "请输入" << g.sum_arc << "个边: ";
	for (int i = 0; i < g.sum_arc; ++i) {
		int s, e;
		cin >> s >> e;
		g.graph[s][e] = g.graph[e][s] = 1;
	}
	return;
}
void print_graph(Graph g) {
	for (int i = 1; i <= g.sum_vex; ++i) {
		for (int j = 1; j <= g.sum_vex; ++j) {
			cout << g.graph[i][j] << " ";
		}
		cout << endl;
	}

}
void DFS(Graph g, int vex) {
	cout << vex << " ";
	vis[vex] = true;
	for (int i = 1; i <= g.sum_vex; ++i) {
		if (g.graph[vex][g.vex[i]] == 0 ||  vis[g.vex[i]] == true)	continue;
		DFS(g, g.vex[i]);
	}
}

struct Node{
	int data;
	Node *next;
};
struct Queue{
	Node *front, *rear;
};
void Init(Queue &Q) {
	Q.front = Q.rear = (Node*)malloc(sizeof(Node));
	Q.front->next = NULL;
	Q.front->data = 0;
}
int Empty(Queue Q) {
	if (Q.front == Q.rear)	return true;
	return false;
}
int Top(Queue Q, int &e) {
	if (Empty(Q))	return -1;
	e = Q.front->next->data;
	return 1;
}
void Push(Queue &Q, int e) {
	Node *p = (Node*)malloc(sizeof(Node));
	p->data = e;
	p->next = NULL;
	Q.rear->next = p;
	Q.rear = p;
	Q.front->data++;
}
int Pop(Queue &Q, int &e) {
	if (Empty(Q))	return -1;
	Node *p;
	p = Q.front->next;
	e = p->data;
	Q.front->next = p->next;
	if (p == Q.rear)	Q.rear = Q.front;
	free(p);
	Q.front->data--;
	return 1;
}

void BFS(Graph g, int vex) {
	for (int i = 1; i <= g.sum_vex; ++i)
		vis[g.vex[i]] = false;
	Queue que;
	Init(que);
	Push(que, vex);
	vis[vex] = true;
	while (!Empty(que)) {
		int top;
		Pop(que, top);
		cout << top << " ";
		for (int i = 1; i <= g.sum_vex; ++i) {
			if (vis[g.vex[i]] || g.graph[top][g.vex[i]] == 0)	continue;
			vis[g.vex[i]] = true;
			Push(que, g.vex[i]);
		}
	}
}
int main() {
	print();
	Graph g;
    int t;
	while (cin >> t) {
		if (t == 5)	break;
		switch (t) {
			case 1:	// 创建
				creat(g);
				break;
			case 2: // 输出
				print_graph(g);
				break;
			case 3: // 深度
				for (int i = 1; i <= g.sum_vex; ++i)
					vis[g.vex[i]] = false;
				DFS(g, g.vex[1]);
				break;
			case 4: // 广度
				BFS(g, g.vex[1]);
				break;

			default:
				printf("输入序号错误! ");
				break;
		}
		printf("\n请输入操作代码：");
	}
	return 0;
}

void print() {
	cout << "**************************************************************\n";
	cout << "******************  1.创建网图              ******************\n";
	cout << "******************  2.输出邻接矩阵          ******************\n";
	cout << "******************  3.深度优先遍历          ******************\n";
	cout << "******************  4.广度优先遍历          ******************\n";
	cout << "******************  5.退出                  ******************\n";
	cout << "请输入你的选择：";
}

无向图的深度优先遍历和广度优先遍历,深度优先,图论,算法