深度学习-必备的数学知识
序言
我们在深度学习-简介和 深度学习-历史背景中已经初步了解的深度学习。在我们真正开始学习深度学习前还需要做些准备工作。那就是学习应用数学和机器学习基础。想要理解深度学习这些是必不可少的。
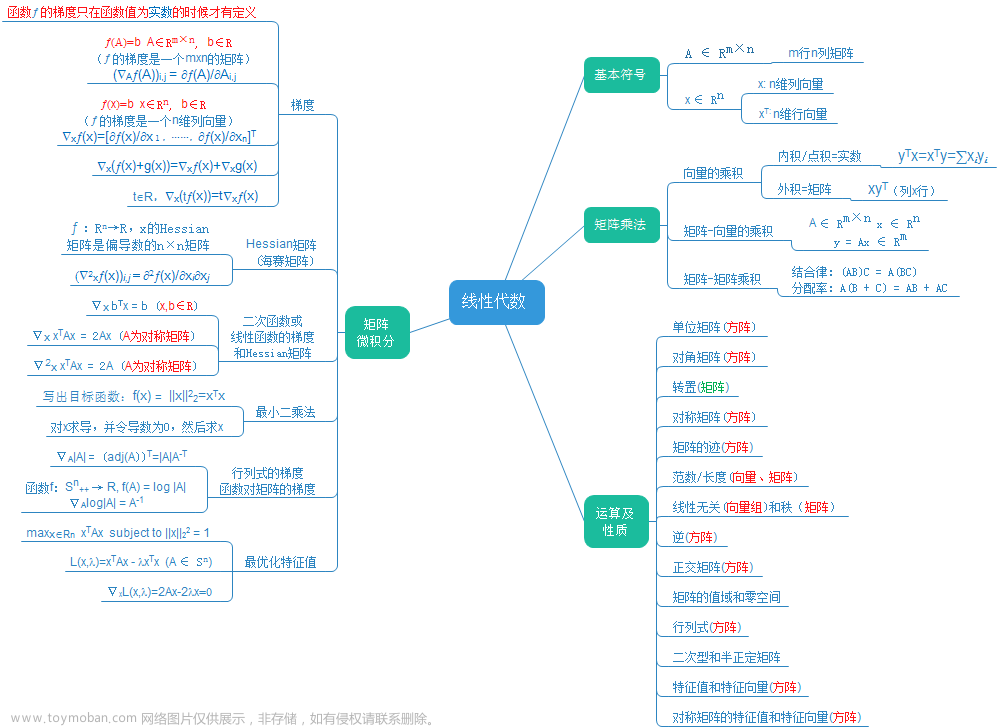
我将在这篇文章中为大家介绍一部分与深度学习有关的线性代数。
线性代数
我们先来了解线性代数中几个重要概念:标量、向量、矩阵、张量
重要概念
- 标量(scalar):标量是一个数。例如:1、2、3。我们使用斜体的小写变量名称表示标量,如 a a a。在定义标量的时候会注明标量属于哪种类型的数。如:在定义实数标量的时候,可能会说 a ∈ R a \in R a∈R表示直线的长度
- 向量(vector):向量是一列数。我们使用粗体的小写变量名称表示向量,如:
x
\mathbf{x}
x.如果向量中有n个元素(数),且每个元素都属于R,我们则称
x
∈
R
n
\mathbf{x} \in R^n
x∈Rn.向量中的数是有序排列的,可以通过索引(次序的位置)获取向量中元素。对于元素我们使用带脚标的斜体表示。如向量中的第一个元素
x
1
x_1
x1,第二个元素
x
2
x_2
x2,第n个元素
x
n
x_n
xn。
我们可以将元素的索引作为一个集合,然后将集合写在脚标处表示向量中所有索引位于集合内的元素。例如:存在向量 x ∈ R 5 \mathbf{x} \in R^5 x∈R5,我们想要索引 x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3。可以定义集合 S = 1 , 2 , 3 S={1,2,3} S=1,2,3。然后写作 x S \mathbf{x}_{S} xS。可以使用-符合表示集合的补集中的索引,如 x − S \mathbf{x}_{-S} x−S表示的是向量 x \mathbf{x} x中除 x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3以外的所有元素构成的向量。
我们可以将向量表示为:
x = [ x 1 x 2 ⋮ x n ] \mathbf{x} = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} x= x1x2⋮xn - 矩阵(matrix):矩阵是二维数组,大家可以将矩阵看成由n个列向量(或者说是一维数组)横向排列构成的。每个列向量都是矩阵的一列。我们使用粗体的大写变量名称表示矩阵。对于具有m行n列,且每个元素都属于R的矩阵,我们写作
A
∈
R
m
×
n
\mathbf{A} \in R^{m\times n}
A∈Rm×n。如矩阵
A
\mathbf{A}
A。同样的我们也可以索引矩阵的元素。对于矩阵
A
\mathbf{A}
A的第i行,第j列的元素,我们表示为
A
i
,
j
A_{i,j}
Ai,j。我们可以使用:符号表示水平坐标或垂直坐标,以表示一行元素或一列元素,如
A
i
,
:
A_{i,:}
Ai,:表示第i行的所有元素,
A
:
,
j
A_{:,j}
A:,j表示第j列的所有元素。我们可以将矩阵表示为
A = [ A 1 , 1 A 1 , 2 A 2 , 1 A 2 , 2 ] \mathbf{A}=\begin{bmatrix} A_{1,1} & A_{1,2} \\ A_{2,1} & A_{2,2} \\ \end{bmatrix} A=[A1,1A2,1A1,2A2,2] - 张量(tensor):一个数组的元素分布在若干维坐标的规则网格中,称之为张量。张量是标量、向量和矩阵概念的扩展。它是可以存放多维数据的数学对象。
0阶张量:标量
1阶张量:向量,也就是一维数组
2阶张量:矩阵,也就是二维数组
n阶张量:n维数组
我们使用 A \mathbf{A} A表示标量,标量 A \mathbf{A} A中坐标维(i,j,k)的元素记作 A i , j , k A_{i,j,k} Ai,j,k。
了解这四个重要概念,我们在来学习可以对它们进行的操作文章来源:https://www.toymoban.com/news/detail-752644.html
操作
转置(transpose)是矩阵的操作之一,矩阵的转置是以主对角线为轴翻转的镜像。主对角线指的是从左上角到右下角的对角线。矩阵的转置会将行变为列,列变为行。m行n列的矩阵
A
∈
R
m
,
n
\mathbf{A} \in R^{m,n}
A∈Rm,n的转置记作
A
T
∈
R
n
,
m
\mathbf{A}^T \in R^{n,m}
AT∈Rn,m。 转置的定义如下:
(
A
T
)
i
,
j
=
A
j
,
i
(\mathbf{A}^T)_{i,j}=\mathbf{A}_{j,i}
(AT)i,j=Aj,i
向量可以看作只有一列的矩阵,所以向量的转置可以看作只有一行的矩阵。我们也可以将一行矩阵转置为列向量,即
[
x
1
,
x
2
,
x
3
]
T
=
x
[x_1,x_2,x_3]^T=x
[x1,x2,x3]T=x。
标量的转置等于它自身。 即
a
T
=
a
a^T=a
aT=a。
我们可以将行数和列数分别相同的两个矩阵进行相加,得到一个新矩阵。新矩阵的元素是两个矩阵对应位置元素相加得到的。形式化地说:如果有两个矩阵
A
∈
R
m
×
n
\mathbf{A} \in R^{m \times n}
A∈Rm×n 和 矩阵
B
∈
R
m
×
n
\mathbf{B} \in R^{m \times n}
B∈Rm×n,我们可以定义一个新矩阵
C
=
A
+
B
\mathbf{C}=\mathbf{A}+\mathbf{B}
C=A+B,其中每个元素
C
i
,
j
=
A
i
,
j
+
B
i
,
j
C_{i,j}=A_{i,j}+B_{i,j}
Ci,j=Ai,j+Bi,j。
标量与矩阵相乘或相加,就是将标量和矩阵的每个元素相乘或相加。形式化得说,如果有两个个标量
a
a
a和
b
b
b和矩阵
A
∈
R
m
×
n
\mathbf{A} \in R^{m \times n}
A∈Rm×n,我们可以定义一个新的矩阵
B
=
a
⋅
A
+
b
\mathbf{B}=a\cdot\mathbf{A}+b
B=a⋅A+b,其中每个元素
B
i
,
j
=
a
⋅
A
i
,
j
+
b
B_{i,j}=a \cdot A_{i,j} + b
Bi,j=a⋅Ai,j+b。
在深度学习中允许向量和矩阵相加,这种操作称为广播(broadcasting)。这种运算中,向量被复制到矩阵的每一行或每一列,然后进行元素级加法运算。
如果我们有一个m行n列的矩阵A和一个长度为n的向量b,我们可以将b添加到A的每一行,得到一个新的矩阵C。形式化地说,我们有
C
=
A
+
b
\mathbf{C}=\mathbf{A}+\mathbf{b}
C=A+b,其中
C
i
,
j
=
A
i
,
j
+
b
j
C_{i,j}=A_{i,j}+b_j
Ci,j=Ai,j+bj。
本系列教程所选教材是深度学习领域奠基性的经典教材《DEEP LEARNING》,它是由LanGoodfello、YoshuaBengio和AraonCourille所撰写。建议有条件的去研读原书,本文章是对这本教材的总结和理解。如有问题,恳请指正。文章来源地址https://www.toymoban.com/news/detail-752644.html
到了这里,关于深度学习-必备的数学知识-线性代数-1的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!