![【Python数据结构与算法】--- 递归算法的应用 ---[乌龟走迷宫] |人工智能|探索扫地机器人工作原理,数据结构与算法,游戏,python,机器人,人工智能,前端,数据结构,算法](https://imgs.yssmx.com/Uploads/2023/12/752756-1.png)
🌈个人主页: Aileen_0v0
🔥系列专栏:PYTHON数据结构与算法学习系列专栏
💫"没有罗马,那就自己创造罗马~"
目录
导言
解决过程
1.建立数据结构
2.探索迷宫:
算法思路
递归调用的“基本结束条件”
3.乌龟走迷宫的实现代码:
运行过程:
拓展:
📝全文总结:
![【Python数据结构与算法】--- 递归算法的应用 ---[乌龟走迷宫] |人工智能|探索扫地机器人工作原理,数据结构与算法,游戏,python,机器人,人工智能,前端,数据结构,算法](https://imgs.yssmx.com/Uploads/2023/12/752756-2.gif)
导言
乌龟探索迷宫这个问题与机器人领域也有关系,
如果我们有一个Roomba扫地机器人,我们或许可以利用乌龟探索迷宫这个问题的解决方法对扫地机器人进行重新编程.
![【Python数据结构与算法】--- 递归算法的应用 ---[乌龟走迷宫] |人工智能|探索扫地机器人工作原理,数据结构与算法,游戏,python,机器人,人工智能,前端,数据结构,算法](https://imgs.yssmx.com/Uploads/2023/12/752756-3.png)
解决过程
首先,要建立数据结构
1.建立数据结构
我们将整个迷宫的空间(矩形)分为行列整齐的方格,区分出墙壁和通道给每个方格具有行列位置,并赋予“墙壁”,"通道”的属性
考虑用矩阵方式来实现迷宫数据结构采用“数据项为字符列表的列表”这种两级列表的方式来保存方格内容
采用不同字符来分别代表“通道为空格 " ,“墙壁我为+”,“海龟投放点S"从一个文本文件逐行读入迷宫数据
2.探索迷宫:
算法思路
龟龟探索迷宫的递归算法思路如下
将海龟从原位置向北移动一步,以新位置递归调用探索迷宫寻找出口;
如果上面的步骤找不到出口,那么将海龟从原位置向南移动一步,以新位置递归调用探索迷宫:
如果向南还找不到出口,那么将海龟从原位置向西移动一步,以新位置递归调用探索迷宫;
如果向西还找不到出口,那么将海龟从原位置向东移动一步,以新位置递归调用探索迷宫;
如果上面四个方向都找不到出口,那么这个迷宫没有出口!
递归调用的“基本结束条件”
归纳如下 :
海龟碰到“墙壁”方格,递归调用结束,返回失败.
海龟碰到“面包屑”方格,表示此方格已访问过递归调用结束,返回失败.
海龟碰到“出口”方格,即“位于边缘的通道”方格,递归调用结束,返回成功!
海龟在四个方向上探索都失败,递归调用结束返回失败
3.乌龟走迷宫的实现代码:
import turtle
#迷宫搜索程序全局常量
START = "S" #--->起始位置
OBSTACLE = "+" #--->墙
TRIED = "." # 走过的路
DEAD_END = "-" # 死路
PART_OF_PATH = "0" # 走出迷宫的出口
#Maze类构造方法
class Maze:
def __init__(self,maze_filename):
with open(maze_filename,"r") as maze_file:
self.maze_list = [
[ch for ch in line.strip("\n")]
for line in maze_file.readlines()
]
self.rows_in_maze = len(self.maze_list)
self.columns_in_maze = len(self.maze_list[0])
for row_idx, row in enumerate(self.maze_list):
if START in row:
self.start_row = row_idx
self.start_col = row.index(START)
break
self.x_translate = -self.columns_in_maze / 2
self.y_translate = self.rows_in_maze / 2
self.t = turtle.Turtle()
self.t.shape("turtle")
self.wn = turtle.Screen()
self.wn.setworldcoordinates(
-(self.columns_in_maze - 1) / 2 - 0.5,
-(self.rows_in_maze - 1) / 2 - 0.5,
(self.columns_in_maze - 1) / 2 + 0.5,
(self.rows_in_maze - 1) / 2 + 0.5,
)
#Maze 类绘制方法
def draw_maze(self):
self.t.speed(10)
self.wn.tracer(0)
for y in range (self.rows_in_maze):
for x in range (self.columns_in_maze):
if self.maze_list[y][x] == OBSTACLE:
self.draw_centered_box(
x + self.x_translate,
-y + self.y_translate,
"orange",
)
self.t.color("black")
self.t.fillcolor("blue")
self.wn.update()
self.wn.tracer(1)
def draw_centered_box(self, x, y, color):
self.t.up()
self.t.goto(x - 0.5, y - 0.5)
self.t.color(color)
self.t.fillcolor(color)
self.t.setheading(90)
self.t.down()
self.t.begin_fill()
for i in range(4):
self.t.forward(1)
self.t.right(90)
self.t.end_fill()
#Maze 类移动方法
def update_position(self,row,col,val=None):
"""标记路径并更新迷宫图景"""
if val:
self.maze_list[row][col] = val
self.move_turtle(col, row)
if val == PART_OF_PATH:
color = "green"
elif val == OBSTACLE:
color = "red"
elif val == TRIED:#已走
color = "black"
elif val == DEAD_END:
color = "red"
else:
color = None
if color:
self.drop_bread_crumb(color)#留下标记物
def move_turtle(self, x, y):
self.t.up()
self.t.setheading(
self.t.towards(
x + self.x_translate,
-y + self.y_translate,
)
)
self.t.goto(
x + self.x_translate, -y + self.y_translate
)
def drop_bread_crumb(self,color):
self.t.dot(10,color)
def is_exit(self, row, col):
"""如果乌龟处于迷宫边缘,表示到达出口"""
return (
row in [0,self.rows_in_maze - 1]
or col in [0,self.columns_in_maze - 1]
)
def __getitem__(self, idx):
return self.maze_list[idx]
def search_from(maze, row, column):
"""对当前位置的四个方向逐一尝试
直至找到出口"""
maze.update_position(row, column)
#检查基本情况:
#1. 遇到了障碍
if maze[row][column] == OBSTACLE:
return False
#2. 遇到已经访问过的位置
if maze[row][column] in [TRIED, DEAD_END]:
return False
#3. 找到了出口
if maze.is_exit(row,column):
maze.update_position(row, column, PART_OF_PATH)
return True
maze.update_position(row, column, TRIED)
#使用逻辑 or 对各个方向进行
#逐一尝试
found = (#利用段路经,逐语句读取 北,南,西,东
search_from(maze, row - 1, column)
or search_from(maze, row + 1, column)
or search_from(maze, row, column-1)
or search_from(maze, row, column+1)
)
if found:
maze.update_position(row, column , PART_OF_PATH)
else:
maze.update_position(row, column , DEAD_END)
return found
my_maze = Maze('maze2.txt')
my_maze.draw_maze()
my_maze.update_position(my_maze.start_row, my_maze.start_col)
search_from(my_maze, my_maze.start_row, my_maze.start_col)运行过程:
![【Python数据结构与算法】--- 递归算法的应用 ---[乌龟走迷宫] |人工智能|探索扫地机器人工作原理,数据结构与算法,游戏,python,机器人,人工智能,前端,数据结构,算法](https://imgs.yssmx.com/Uploads/2023/12/752756-4.gif)
拓展:
在死胡同里乌龟的是如何走的呢?
![【Python数据结构与算法】--- 递归算法的应用 ---[乌龟走迷宫] |人工智能|探索扫地机器人工作原理,数据结构与算法,游戏,python,机器人,人工智能,前端,数据结构,算法](https://imgs.yssmx.com/Uploads/2023/12/752756-5.gif)
📝全文总结:
这篇文章主要讲解的是,如何用递归算法解决乌龟🐢走迷宫问题,这个问题类似于我们的扫地机器人,但是这个算法存在这一写缺点,比如说 时间方面和距离方面.如果我们要利用这个算法来写机器人我们可以从记录的路径信息,对机器人进行重新编程,以便它可以在较少的时间内清理地面,并优化其行进路线。
![【Python数据结构与算法】--- 递归算法的应用 ---[乌龟走迷宫] |人工智能|探索扫地机器人工作原理,数据结构与算法,游戏,python,机器人,人工智能,前端,数据结构,算法](https://imgs.yssmx.com/Uploads/2023/12/752756-6.gif) 文章来源:https://www.toymoban.com/news/detail-752756.html
文章来源:https://www.toymoban.com/news/detail-752756.html
![【Python数据结构与算法】--- 递归算法的应用 ---[乌龟走迷宫] |人工智能|探索扫地机器人工作原理,数据结构与算法,游戏,python,机器人,人工智能,前端,数据结构,算法](https://imgs.yssmx.com/Uploads/2023/12/752756-7.gif) 文章来源地址https://www.toymoban.com/news/detail-752756.html
文章来源地址https://www.toymoban.com/news/detail-752756.html
到了这里,关于【Python数据结构与算法】--- 递归算法的应用 ---[乌龟走迷宫] |人工智能|探索扫地机器人工作原理的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!



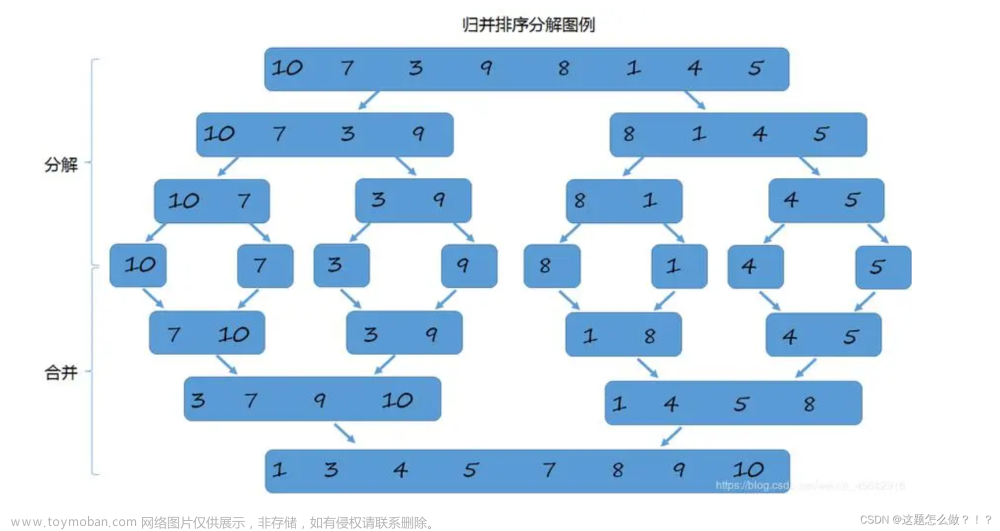


![[数据结构 -- 手撕排序算法第七篇] 递归实现归并排序](https://imgs.yssmx.com/Uploads/2024/02/573259-1.png)