【手撕数据结构】二分查找(好多细节)-Toy模板网

这篇具有很好参考价值的文章主要介绍了【手撕数据结构】二分查找(好多细节)。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

🌈键盘敲烂，年薪30万🌈

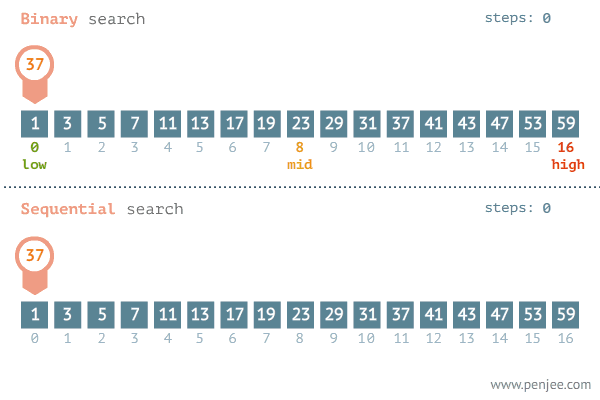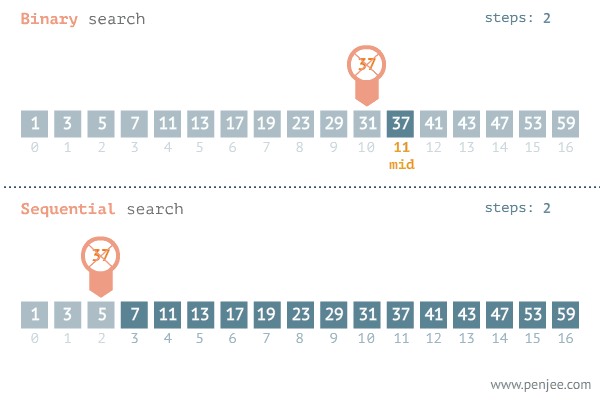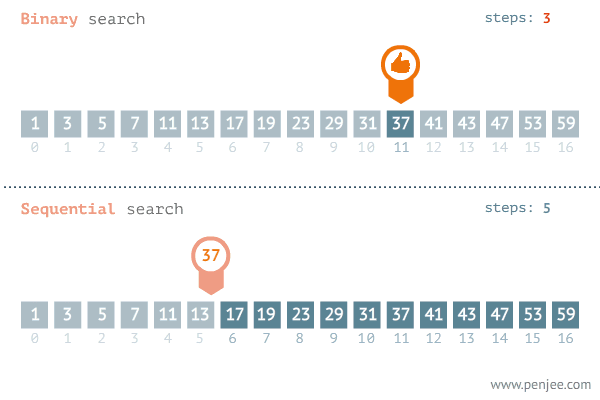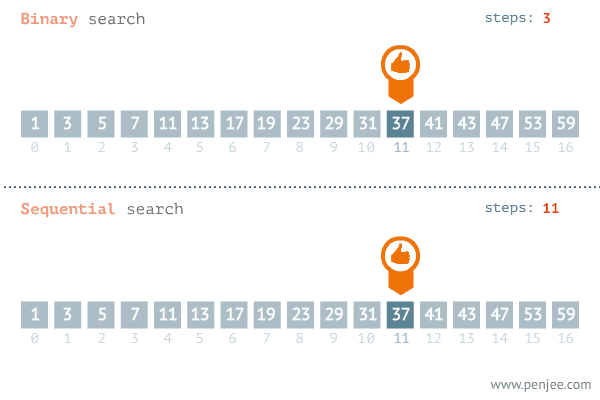
普通版本的二分查找：

right只负责控制边界(少了两次比较)：

时间复杂度更稳定的版本：

BSLeftmost：

BSRightmost：

文章来源地址https://www.toymoban.com/news/detail-752849.html

普通版本的二分查找：

🏸细节1：循环判定条件是left <= right
⭐细节2：mid = (left + right ) >>> 1 原因见代码注释


/***
 * 二分查找的实现 3个版本
 * 时间复杂度：O（longn）
 * 空间复杂度：O（1）
 *
 * 细节1：循环判定条件是left <= right
 * 细节2：mid计算要用 >>> 因为left + right 可能越界
 *      例如：right = Integer.MAX_INT-1 left = 0;
 *      第一轮计算没问题 假设mid < target
 *      left = mid + 1; 这是后left+ right 就超出int的最大范围，变成负数
 *      原因很简单：java没有无符号数，最高位表示符号位，/ 运算是先将补码转原码 >>>位运算是直接再二进制上运算
 */
public class Demo1 {
    public static void main(String[] args) {
        int[] nums = {1,4,6,8,15,76,145};
        int target = 145;
        int index1 = method1(nums, target);
        System.out.println(target + "索引为" + index1);
        System.out.println(target + "索引为" + index2);
    }

    private static int method1(int[] nums, int target) {
        int left = 0, right = nums.length-1;
        while(left <= right){
            //细节 用无符号右移运算符
            int mid = (left + right) >>> 1;
            if(nums[mid] > target){
                right = mid - 1;
            }else if (nums[mid] < target){
                left = mid + 1;
            }else{
                return mid;
            }
        }
        return -1;
    }
}

right只负责控制边界(少了两次比较)：

改动1：while条件是left < right
改动2：right = nums.length

public class Demo1 {
    public static void main(String[] args) {
        int[] nums = {1,4,6,8,15,76,145};
        int target = 145;
        int index2 = method2(nums, target);
        System.out.println(target + "索引为" + index2);
    }
}
    private static int method2(int[] nums, int target) {
        int left = 0, right = nums.length; //right 只代表有边界，不参与比较
        while(left < right){
            int mid = (left + right) >>> 1;
            if(nums[mid] < target){
                left = mid + 1;
            }else if(nums[mid] > target){
                right = mid;
            }else {
                return mid;
            }
        }
        return -1;
    }

时间复杂度更稳定的版本：

细节：减少了if比较次数

public class Demo1 {
    public static void main(String[] args) {
        int[] nums = {1,4,6,8,15,76,145};
        int target = 145;
        int index3 = method3(nums, target);
        System.out.println(target + "索引为" + index3);
    }
}    
    private static int method3(int[] nums, int target) {
        //这个最牛逼
        //减少循环内的比较次数
        int left = 0, right = nums.length;
        while(1 < right - left){
            int mid = (left + right) >>> 1;
            if(nums[mid] > target){
                right = mid;
            }else{
                left = mid;
            }
        }
        if(nums[left] == target){
            return left;
        }
        return -1;
    }

BSLeftmost：

/**
 *
 * 应用：求成绩排名  求前任
 */
public class Leftmost {
    public static void main(String[] args) {
        int[] nums = {1,2,4,4,4,6,7};
        int target = 3;
        /***
         * params
         * return 找到了 - 返回靠左的下标
         *        没找到 - 返回>target的最靠左下标
         */
        int ans = BSLeftmost(nums, target);
        System.out.println(ans);

    }

    private static int BSLeftmost(int[] nums, int target) {
        int left = 0, right = nums.length -1;
        while(left <= right){
            int mid = (left+right) >>> 1;
            if(target > nums[mid]){
                left = mid + 1;
            } else{
                right = mid - 1;
            }
        }
        return left;
    }
}

BSRightmost：

/**
 *
 * 求后任
 */
public class Rightmost {
    public static void main(String[] args) {
        int[] nums = {1,2,4,4,4,6,7};
        int target = 3;
        /**
         * return 找到了返回下标
         *        没找到返回 <= targer的最靠右索引
         *
         */
        int ans = BSRightmost(nums, target);
        System.out.println(ans);
    }

    private static int BSRightmost(int[] nums, int target) {
        int left = 0, right = nums.length-1;
        while(left <= right){
            int mid = (left + right) >>> 1;
            if(target >= nums[mid]){
                left = mid + 1;
            }else {
                right = mid - 1;
            }
        }
        return left - 1;
    }
}

到了这里，关于【手撕数据结构】二分查找(好多细节)的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！