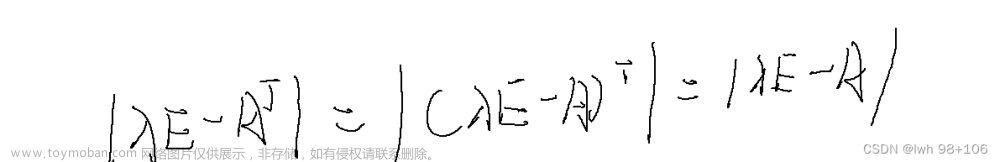特征值与特征向量
矩阵 A \mathbf A A的特征值与特征向量满足 A x = λ x \mathbf A\mathbf x=\lambda\mathbf x Ax=λx,即 ( A − λ I ) x = 0 (\mathbf A-\lambda\mathbf I)\mathbf x=0 (A−λI)x=0,且 x ≠ 0 \mathbf x\neq0 x=0
-
特征值:
d
e
t
(
A
−
λ
I
)
=
0
det(\mathbf A-\lambda\mathbf I)=0
det(A−λI)=0的根,其中
p
(
λ
)
=
d
e
t
(
A
−
λ
I
)
p(\lambda)=det(\mathbf A-\lambda\mathbf I)
p(λ)=det(A−λI)为特征多项式
A \mathbf A A全体所有特征值也称为 A \mathbf A A的谱,记为 λ ( A ) \lambda(\mathbf A) λ(A) - 特征向量: ( A − λ I ) x = 0 (\mathbf A-\lambda\mathbf I)\mathbf x=0 (A−λI)x=0的非零解,可见特征向量可能充满一整个子空间,该子空间就是零空间 N ( A − λ I ) N(\mathbf A-\lambda\mathbf I) N(A−λI),称为特征子空间
不同特征值对应的特征子空间的交为{0}
相关的小技巧:若 A \mathbf A A的特征值为 λ \lambda λ,则 A − k I \mathbf A-k\mathbf I A−kI的特征值为 λ − k \lambda-k λ−k
代数重数与几何重数
首先注意,代数重数与几何重数的概念,都是针对某一个特征值 λ i \lambda_i λi而言的
将
n
n
n阶矩阵
A
\mathbf A
A的特征多项式写为
p
(
t
)
=
det
(
A
−
t
I
)
=
(
λ
1
−
t
)
β
1
⋯
(
λ
k
−
t
)
β
k
p(t)=\operatorname{det}(A-t I)=\left(\lambda_{1}-t\right)^{\beta_{1}} \cdots\left(\lambda_{k}-t\right)^{\beta_{k}}
p(t)=det(A−tI)=(λ1−t)β1⋯(λk−t)βk
其中,
β
1
+
β
2
+
.
.
.
β
k
=
n
\beta_1+\beta_2+...\beta_k=n
β1+β2+...βk=n(
n
n
n阶多项式,有
n
n
n个根)
- 特征值
λ
i
\lambda_i
λi的代数重数为
β
i
\beta_i
βi
ps. 代数重数也可以定义为 β i = d i m [ N ( ( A − λ i I ) n ) ] \beta_i=dim[N((\mathbf A-\lambda_i\mathbf I)^n)] βi=dim[N((A−λiI)n)],见特征值的代数重数与几何重数 - 特征值 λ i \lambda_i λi的几何重数为其特征子空间的维数,即 d i m [ N ( A − λ i I ) ] dim[N(\mathbf A-\lambda_i\mathbf I)] dim[N(A−λiI)]
对于任一特征值 λ i \lambda_i λi,几何重数<=代数重数
- 当特征值有重根时,就可能有几何重数<代数重数,此时“缺少”特征向量,对应降维变换,并且矩阵无法相似对角化
相似对角化和Jordan标准型
- 当所有特征值的几何重数=代数重数,有
d
i
m
[
N
(
A
−
λ
1
I
)
]
+
.
.
.
+
d
i
m
[
N
(
A
−
λ
k
I
)
]
=
n
dim[N(\mathbf A-\lambda_1\mathbf I)]+...+dim[N(\mathbf A-\lambda_k\mathbf I)]=n
dim[N(A−λ1I)]+...+dim[N(A−λkI)]=n,矩阵可相似对角化:
可以用 n n n个线性无关的特征向量组成可逆矩阵 P \mathbf P P,使 A = P Λ P − 1 \mathbf A=\mathbf P\mathbf \Lambda\mathbf P^{-1} A=PΛP−1
此时, A \mathbf A A的特征向量可以给出 C n \mathbb{C}^{n} Cn空间的一组基
或者说, A \mathbf A A的所有特征子空间给出了整个空间的直和分解: N ( A − λ 1 I ) ⊕ ⋯ ⊕ N ( A − λ k I ) = C n N\left(A-\lambda_{1} I\right) \oplus \cdots \oplus N\left(A-\lambda_{k} I\right)=\mathbb{C}^{n} N(A−λ1I)⊕⋯⊕N(A−λkI)=Cn
实对称矩阵(n个正交的特征向量)、幂等矩阵(证明见后文)必然可以相似对角化
- 更一般的,矩阵没有
n
n
n个线性无关的特征向量,则无法相似对角化,此时只能求Jordan标准型
J
\mathbf J
J,使
A
=
P
J
P
−
1
\mathbf A=\mathbf P\mathbf J\mathbf P^{-1}
A=PJP−1
此时仅满足 d i m [ N ( ( A − λ 1 I ) n ) ] + . . . + d i m [ N ( ( A − λ k I ) n ) ] = n dim[N((\mathbf A-\lambda_1\mathbf I)^n)]+...+dim[N((\mathbf A-\lambda_k\mathbf I)^n)]=n dim[N((A−λ1I)n)]+...+dim[N((A−λkI)n)]=n(代数重数的定义2)
定义特征值 λ i \lambda_i λi的广义特征向量为 ( A − λ I ) n x = 0 (\mathbf A-\lambda\mathbf I)^n\mathbf x=0 (A−λI)nx=0的非零解,
将 N ( ( A − λ i I ) n ) N((\mathbf A-\lambda_i\mathbf I)^n) N((A−λiI)n)称为广义特征子空间(其维数=代数重数, β i = d i m [ N ( ( A − λ i I ) n ) ] \beta_i=dim[N((\mathbf A-\lambda_i\mathbf I)^n)] βi=dim[N((A−λiI)n)])
那么,可以用 n n n个线性无关的广义特征向量组成可逆矩阵 P \mathbf P P,使 A = P J P − 1 \mathbf A=\mathbf P\mathbf J\mathbf P^{-1} A=PJP−1,见Jordan 标准型-寻找广义特征向量
此时,广义特征子空间给出了整个空间的直和分解: N ( ( A − λ 1 I ) n ) ⊕ ⋯ ⊕ N ( ( A − λ k I ) n ) = C n N\left(\left(A-\lambda_{1} I\right)^{n}\right) \oplus \cdots \oplus N\left(\left(A-\lambda_{k} I\right)^{n}\right)=\mathbb{C}^{n} N((A−λ1I)n)⊕⋯⊕N((A−λkI)n)=Cn文章来源:https://www.toymoban.com/news/detail-753173.html
例题:证明幂等矩阵一定可以相似对角化
对于幂等矩阵
P
\mathbf P
P有
P
2
=
P
\mathbf P^2=\mathbf P
P2=P,幂等矩阵的特征值只可能为0和1(由
P
x
=
λ
x
\mathbf P\mathbf x=\lambda\mathbf x
Px=λx和
P
2
x
=
λ
2
x
\mathbf P^2\mathbf x=\lambda^2\mathbf x
P2x=λ2x可知)
另外,
(
I
−
P
)
\mathbf {(I-P)}
(I−P)也是幂等矩阵(
(
I
−
P
)
2
=
I
−
P
\mathbf {(I-P)^2}=\mathbf {I-P}
(I−P)2=I−P)
因此有
N
(
P
n
)
=
N
(
P
)
N(\mathbf P^n)=N(\mathbf P)
N(Pn)=N(P)和
N
(
(
I
−
P
)
n
)
=
N
(
I
−
P
)
N(\mathbf{(I-P)}^n)=N(\mathbf {I-P})
N((I−P)n)=N(I−P),由上面的知识,特征值0的代数重数等于几何重数,特征值1的代数重数也等于几何重数,故幂等矩阵一定可以相似对角化文章来源地址https://www.toymoban.com/news/detail-753173.html
到了这里,关于矩阵理论| 基础:特征值与特征向量、代数重数/几何重数、相似对角化和Jordan标准型的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!