二叉树(binary tree)是指树中节点的度不大于2的有序树,它是一种最简单且最重要的树。二叉树的递归定义为:二叉树是一棵空树,或者是一棵由一个根节点和两棵互不相交的,分别称作根的左子树和右子树组成的非空树;左子树和右子树又同样都是二叉树。以下是对链式存储结构的二叉树的创建与先序、中序、后序遍历操作:
定义二叉树节点
每个节点由三个部分组成:
数据部分
左孩子节点
右孩子节点
typedef struct BiTNode{
ElemType data;
struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
主函数
声明初始节点时,是BiTree bt,此时bt是节点指针,如果写的是BiTNode bt,则为节点元素。为了传地址操作方便,我们使用声明节点地址的形式。
int main(){
BiTree bt;//指针
initial(&bt);
cout<<"先序创建树(输入#停止生成节点):\n";
createTree(&bt);
cout<<"先序遍历:\n";
preOrder(bt);
cout<<"\n中序遍历:\n";
inOrder(bt);
cout<<"\n后序遍历:\n";
postOrder(bt);
return 0;
}
初始化
我们在主函数里以initial(&bt)的形式调用bt指针,即将指针地址传入初始化函数里。参数里写的是(BiTree bt)表示bt是指向根节点这个节点指针的指针。
此时bt指的是根节点指针,(BiTree)malloc(sizeof(BiTNode))为该节点分配空间。
初始时均无左右孩子,所以设为NULL。
Status initial(BiTree *bt){//指针的指针
*bt = (BiTree)malloc(sizeof(BiTNode));
(*bt)->lchild = NULL;
(*bt)->rchild = NULL;
}
创建二叉树
依然是以指针的指针的形式将节点指针传入函数里
我们设置输入“#”为输入结束。
当输入的元素不是“#”时,为节点指针开辟空间后,将元素赋给该节点的data。
然后递推式创建左右孩子。
Status createTree(BiTree *bt){
ElemType c;
c = getchar();
if(c=='#'){
*bt = NULL;
}else{
*bt = (BiTree)malloc(sizeof(BiTNode));
(*bt)->data = c;
createTree(&(*bt)->lchild);
createTree(&(*bt)->rchild);
}
}
值得注意的是:因为我们使用的是“指针的指针”,所以递推式将创建其左右孩子时,记得是将其左右孩子的地址传入createTree函数里
(即:&(*bt)->child的形式)
关于先序、中序和后序遍历
先序遍历最容易理解:从根节点开始输出,一直向左遍历输出,到尽头后再找到该节点兄弟右节点输出,然后再去到父亲节点的兄弟右节点输出……以此类推。
中序遍历:从左子树的最左边最底层的左孩子节点开始输出,然后输出其父亲节点,再输出其兄弟右节点,然后输出其父亲节点的父亲节点……以此类推。
后序遍历:从左子树的最左边最底层的左孩子节点开始输出,然后输出其兄弟右节点,然后输出其父亲节点,然后输出其父亲节点的熊迪右节点……以此类推。
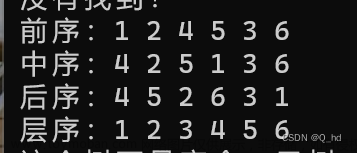
示例1
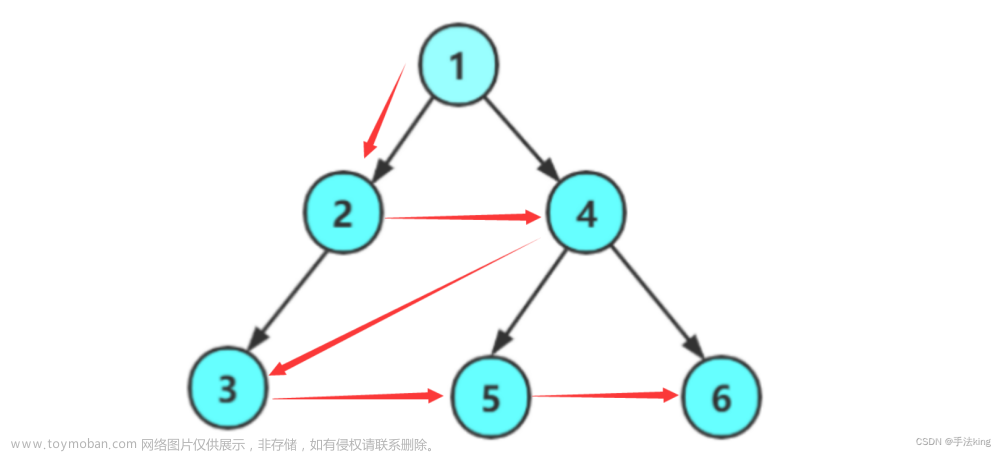
我们来创建一个如下图的树:

示例2


示例3



简单粗暴地画法就是遵守这个规律: 文章来源:https://www.toymoban.com/news/detail-753254.html
文章来源:https://www.toymoban.com/news/detail-753254.html
先序、中序、后序遍历代码实现:
void preOrder(BiTree bt){//指针形参
if(bt!=NULL){
cout<<bt->data<<" ";
preOrder(bt->lchild);
preOrder(bt->rchild);
}
}
void inOrder(BiTree bt){//指针形参
if(bt!=NULL){
inOrder(bt->lchild);
cout<<bt->data<<" ";
inOrder(bt->rchild);
}
}
void postOrder(BiTree bt){//指针形参
if(bt!=NULL){
postOrder(bt->lchild);
postOrder(bt->rchild);
cout<<bt->data<<" ";
}
}
源代码(编程风格参考严蔚敏版《数据结构》)
#include<iostream>
#include<stdio.h>
#include<malloc.h>
using namespace std;
#define MAXSIZE 5
#define ElemType char
#define Status int//表示状态
#define OK 1
#define ERROR 0
#define STOP 0
#define OVERFLOW 0
typedef struct BiTNode{
ElemType data;
struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
Status initial(BiTree *bt){//指针的指针
*bt = (BiTree)malloc(sizeof(BiTNode));
(*bt)->lchild = NULL;
(*bt)->rchild = NULL;
}
Status createTree(BiTree *bt){
ElemType c;
c = getchar();
if(c=='#'){
*bt = NULL;
}else{
*bt = (BiTree)malloc(sizeof(BiTNode));
(*bt)->data = c;
createTree(&(*bt)->lchild);
createTree(&(*bt)->rchild);
}
}
void preOrder(BiTree bt){//指针形参
if(bt!=NULL){
cout<<bt->data<<" ";
preOrder(bt->lchild);
preOrder(bt->rchild);
}
}
void inOrder(BiTree bt){//指针形参
if(bt!=NULL){
inOrder(bt->lchild);
cout<<bt->data<<" ";
inOrder(bt->rchild);
}
}
void postOrder(BiTree bt){//指针形参
if(bt!=NULL){
postOrder(bt->lchild);
postOrder(bt->rchild);
cout<<bt->data<<" ";
}
}
int main(){
BiTree bt;//指针
initial(&bt);
cout<<"先序创建树(输入#停止生成节点):\n";
createTree(&bt);
cout<<"先序遍历:\n";
preOrder(bt);
cout<<"\n中序遍历:\n";
inOrder(bt);
cout<<"\n后序遍历:\n";
postOrder(bt);
return 0;
}
敬请批评指正!文章来源地址https://www.toymoban.com/news/detail-753254.html
到了这里,关于数据结构——二叉树的创建与遍历(链式存储结构)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!