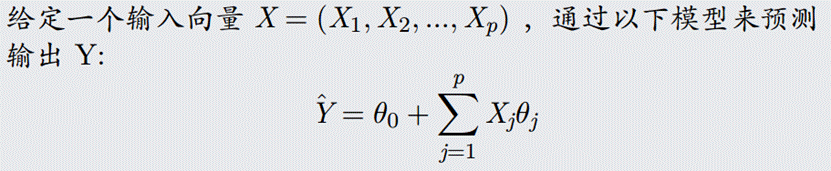本文为学习吴恩达版本机器学习教程的代码整理,使用的数据集为https://github.com/fengdu78/Coursera-ML-AndrewNg-Notes/blob/f2757f85b99a2b800f4c2e3e9ea967d9e17dfbd8/code/ex1-linear%20regression/ex1data1.txt
将数据集和py代码放到同一目录中,使用Spyder打开运行,代码中整体演示了数据加载处理过程、线性回归损失函数计算方法、批量梯度下降方法、获得结果后的预估方法、线性回归结果函数绘制、模型导出及加载使用方法,其中最后三部分彼此无依赖关系可单独执行。详细代码为下:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import joblib
# 导入数据
path = 'ex1data1.txt'
data = pd.read_csv(path, header=None, names=['Population', 'Profit'])
"""
计算线性回归模型的损失值
"""
def computeCost(X, y, theta):
"""
此函数计算给定参数 theta 下的均方误差损失。它用于评估线性回归模型预测值与实际值之间的差异。
损失值越小,表明模型的预测越准确。
Parameters:
X : numpy.ndarray 表示特征数据集的矩阵,其中包含了模型用于预测的特征。
y : numpy.ndarray 表示目标变量的向量,包含了每个数据点的实际值。
theta : numpy.ndarray 线性回归模型的参数向量,包括截距项和特征的系数。
Returns:
float 返回计算得到的均方误差损失值。
"""
# 计算模型预测值和实际值之间的差异
inner = np.power(((X * theta.T) - y), 2)
# 计算并返回均方误差损失的平均值
return np.sum(inner) / (2 * len(X))
# 在数据集前面加入一列全为1的数据,用于适配截距项
data.insert(0, 'Ones', 1)
# 分离特征(X)和目标变量(y)
cols = data.shape[1]
X = data.iloc[:,0:cols-1]#X是所有行,去掉最后一列
y = data.iloc[:,cols-1:cols]#X是所有行,最后一列
# 将X和y的类型转换为numpy矩阵,方便后续计算
X = np.matrix(X.values)
y = np.matrix(y.values)
theta = np.matrix(np.array([0,0]))# 初始化theta
# 计算初始的损失值,仅为输出和最终损失对比
initial_cost = computeCost(X, y, theta)
print("初始的损失值:", initial_cost)
"""
执行批量梯度下降
"""
def gradientDescent(X, y, theta, alpha, iters):
"""
这个函数通过迭代地调整参数 theta,以最小化损失函数。
Parameters:
X : numpy.ndarray 特征数据集矩阵。
y : numpy.ndarray 目标变量向量。
theta : numpy.ndarray 线性回归模型的初始参数向量。
alpha : float 学习率,控制梯度下降的步长。
iters : int 梯度下降的迭代次数。
Returns:
tuple 返回一个元组,包含优化后的 theta 和每次迭代的损失值数组。
"""
# 初始化一个临时变量,用于更新 theta
temp = np.matrix(np.zeros(theta.shape))
# 获取 theta 中参数的数量
parameters = int(theta.ravel().shape[1])
# 初始化一个数组,用于记录每次迭代的损失值
cost = np.zeros(iters)
# 迭代进行梯度下降
for i in range(iters):
# 计算当前参数下的误差
error = (X * theta.T) - y
# 对每个参数进行更新
for j in range(parameters):
# 计算误差与特征值的乘积
term = np.multiply(error, X[:,j])
# 更新 theta 的第 j 个参数
temp[0,j] = theta[0,j] - ((alpha / len(X)) * np.sum(term))
# 更新 theta
theta = temp
# 记录当前的损失值
cost[i] = computeCost(X, y, theta)
# 返回优化后的参数和损失值记录
return theta, cost
# 设置学习率和迭代次数
alpha = 0.01
iters = 2000
# 执行梯度下降算法,优化theta
g, cost = gradientDescent(X, y, theta, alpha, iters)
# 计算优化后的损失值,仅为输出和初始损失对比
final_cost = computeCost(X, y, g)
print("优化后的损失值", final_cost)
"""
使用需要预测的数据X进行预测
"""
# 假设的人口数据
population_values = [3.5, 7.0] # 代表35,000和70,000人口
# 对每个人口值进行预测
for pop in population_values:
# 将人口值转换为与训练数据相同的格式(包括截距项)
predict_data = np.matrix([1, pop]) # 添加截距项
# 使用模型进行预测
predict_profit = np.dot(predict_data, g.T)
print(f"模型预测结果 {pop} : {predict_profit[0,0]}")
"""
使用模型绘制函数
"""
# 创建预测函数
x = np.linspace(data.Population.min(), data.Population.max(), 100)
f = g[0, 0] + (g[0, 1] * x)
# 绘制线性回归结果
fig, ax = plt.subplots(figsize=(12,8))
ax.plot(x, f, 'r', label='Prediction')# 绘制预测线
ax.scatter(data.Population, data.Profit, label='Traning Data')# 绘制训练数据点
ax.legend(loc=2)
ax.set_xlabel('Population')
ax.set_ylabel('Profit')
ax.set_title('Predicted Profit vs. Population Size')
plt.show()
"""
使用模型绘制损失值变化曲线
"""
# 绘制损失函数的变化
fig, ax = plt.subplots(figsize=(12,8))
ax.plot(np.arange(iters), cost, 'r') # 损失值随迭代次数的变化
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title('Error vs. Training Epoch')
plt.show()
"""
保存模型
"""
# 保存模型
joblib.dump(g, 'linear_regression_model.pkl')
"""
加载模型并执行预测
"""
# 加载模型
loaded_model = joblib.load('linear_regression_model.pkl')
# 假设的人口数据
population_values = [3.5, 7.0] # 代表35,000和70,000人口
# 使用模型进行预测
for pop in population_values:
# 更新预测数据矩阵,包括当前的人口值
predict_data = np.matrix([1, pop])
# 进行预测
predict_value = np.dot(predict_data, loaded_model.T)
print(f"加载模型预测结果 {pop} : {predict_value[0,0]}")
运行后结果:

输出结果:文章来源:https://www.toymoban.com/news/detail-753351.html
初始的损失值: 32.072733877455676
优化后的损失值 4.47802760987997
模型预测结果 3.5 : 0.349676138927709
模型预测结果 7.0 : 4.487420850578528
加载模型预测结果 3.5 : 0.349676138927709
加载模型预测结果 7.0 : 4.487420850578528
上一个版本的线性回归算法是依据批量梯度下降公式过程计算出来的,但实际上直接使用矩阵来计算能够极大提升效率,代码如下:文章来源地址https://www.toymoban.com/news/detail-753351.html
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import joblib
# 导入数据
path = 'ex1data1.txt'
data = pd.read_csv(path, header=None, names=['Population', 'Profit'])
# 分离特征和目标变量
X = data.iloc[:, 0:1].values # Population列
y = data.iloc[:, 1].values # Profit列
m = len(y) # 样本数量
# 添加一列全为1的截距项
X = np.append(np.ones((m, 1)), X, axis=1)
# 初始化模型参数
theta = np.zeros(2)
# 批量梯度下降参数
alpha = 0.01 # 学习率
iterations = 1500 # 迭代次数
# 批量梯度下降算法
def gradientDescent(X, y, theta, alpha, num_iters):
m = len(y) # 获取样本数量
for i in range(num_iters): # 对于指定的迭代次数
# 计算当前theta下的预测值。这是通过矩阵X(特征)和theta(参数)的点积来完成的。
predictions = X.dot(theta)
# 计算预测值和实际值之间的误差。
errors = np.subtract(predictions, y)
# 计算梯度:首先,计算特征矩阵X的转置和误差的点积;
# 然后,乘以学习率alpha和样本数量的倒数。
sum_delta = (alpha / m) * X.transpose().dot(errors)
# 更新参数theta:从当前theta中减去梯度(乘以学习率)。
theta = theta - sum_delta
return theta # 在完成所有迭代后,返回最终的参数theta。
# 进行梯度下降以拟合模型
theta = gradientDescent(X, y, theta, alpha, iterations)
"""
使用需要预测的数据X进行预测
"""
# 假设的人口数据
population_values = [3.5, 7.0] # 代表35,000和70,000人口
# 对每个人口值进行预测
for pop in population_values:
# 将人口值转换为与训练数据相同的格式(包括截距项)
predict_data = np.matrix([1, pop]) # 添加截距项
# 使用模型进行预测
predict_profit = np.dot(predict_data, theta.T)
print(f"模型预测结果 {pop} : {predict_profit[0,0]}")
"""
使用模型绘制函数
"""
# 创建预测函数
x_values = np.array(X[:, 1])
f = theta[0] + (theta[1] * x_values)
# 绘制图表
fig, ax = plt.subplots(figsize=(12, 8))
ax.plot(x_values, f, 'r', label='Prediction')
ax.scatter(data.Population, data.Profit, label='Training Data')
ax.legend(loc=2)
ax.set_xlabel('Population')
ax.set_ylabel('Profit')
ax.set_title('Predicted Profit vs. Population Size')
plt.show()
"""
保存模型
"""
# 保存模型
joblib.dump(theta, 'linear_regression_model.pkl')
"""
加载模型并执行预测
"""
# 加载模型
loaded_model = joblib.load('linear_regression_model.pkl')
# 假设的人口数据
population_values = [3.5, 7.0] # 代表35,000和70,000人口
# 使用模型进行预测
for pop in population_values:
# 更新预测数据矩阵,包括当前的人口值
predict_data = np.matrix([1, pop])
# 进行预测
predict_value = np.dot(predict_data, loaded_model.T)
print(f"模型预测结果 {pop} : {predict_value[0,0]}")
到了这里,关于单变量线性回归的机器学习代码的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!