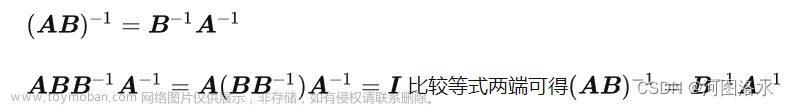MIT线性代数笔记-第27讲-复数矩阵，快速傅里叶变换-Toy模板网

这篇具有很好参考价值的文章主要介绍了MIT线性代数笔记-第27讲-复数矩阵，快速傅里叶变换。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

27.复数矩阵，快速傅里叶变换

对于实矩阵而言，特征值为复数时，特征向量一定为复向量，由此引入对复向量的学习

求模长及内积

假定一个复向量 $\vec{z} = \begin{bmatrix} z_1 \\ z_2 \\ \vdots\\ z_n \end{bmatrix}$ ，其中 $z_1 , z_2 , \cdots , z_n$ 为复数，所以该向量不再属于 $R^n$ ，而是属于 $n$ 维复空间 $C^n$

显然再使用 $\sqrt{\vec{z}^T \vec{z}}$ 无法求出模长，比如对于 $\vec{z} = \begin{bmatrix} 1 \\ i \end{bmatrix}$ 有 $\sqrt{\vec{z}^T \vec{z}} = \begin{bmatrix} 1 & i \end{bmatrix} \begin{bmatrix} 1 \\ i \end{bmatrix} = 0 \ne \sqrt{2}$

由上一讲的内容可以得到 $|\vec{z}| = \sqrt{\overline{\vec{z}}^T \vec{z}}$ ，我们把求共轭和转置两步操作一起记作 $H$ （来自 $Her mi t e$ ），即 $\vec{z}^H = \overline{\vec{z}}^T$

同理，求内积时也使用 $H$ ，即对于两个复向量 $\vec{x} , \vec{y}$ ，有 $\vec{x} \cdot \vec{y} = \vec{x}^H \vec{y}$ ，此时内积为 $0$ 仍然可以说明向量正交，对于矩阵也类似
对称矩阵的推广

对于实矩阵，对称矩阵即满足 $A^T = A$ 的矩阵，推广到复矩阵，我们把满足 $A^H = A$ 的矩阵称作厄米特矩阵

可以发现厄米特矩阵的对角线元素均为实数，因为它们在转置时不变，所以在求共轭时也不变，其它元素与转置后的对应元素互为共轭

由上一讲可知厄米特矩阵的特征值一定为实数
正交矩阵的推广

对于实矩阵，正交矩阵即满足 $Q^T Q = I$ 的方阵，推广到复矩阵，我们把满足 $Q^H Q= I$ 的方阵称作酉矩阵

可以发现酉矩阵的列向量组成复空间下的一组标准正交基，其转置与正交一致且均为酉矩阵
傅里叶矩阵

傅里叶变换是一种分析信号的方法，它可分析信号的成分，也可用这些成分合成信号。许多波形可作为信号的成分，比如正弦波、方波、锯齿波等，傅里叶变换用正弦波作为信号的成分。由于傅里叶变换经常用在计算机上，而在电子工程或计算机中，方阵的行和列都是从 $0$ 开始到 $n - 1$ 结束的，所以在讨论傅里叶矩阵时遵从这种下标规则。

傅里叶矩阵是一种酉矩阵，它满足 $(F_n)_{i , j} = \dfrac{1}{n} w^{i * j} , i , j = 0 , \cdots , n - 1$ （ $e^{2 \pi i / n}$ ），即：

$F_n = \dfrac{1}{n} \begin{bmatrix} 1 & 1 & 1 & \cdots & 1 \\ 1 & w & w^2 & \cdots & w^{n - 1} \\ 1 & w^2 & w^4 & \cdots & w^{2(n - 1)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & w^{n - 1} & w^{2(n - 1)} & \cdots & w^{(n - 1)^2} \end{bmatrix}$

可以发现 $e^{2 \pi i / n} = cos\ \dfrac{2 \pi}{n} + i sin\ \dfrac{2 \pi}{n}$ ，落在复平面原点为圆心的单位圆上，且对应的角度为一圈的 $\dfrac{1}{n}$ ，所以 $w$ 乘上自己相当于增加角度 $\dfrac{2 \pi}{n}$ ，因此 $w^{kn} = (w^n)^k = 1 , k \in Z$

证明傅里叶矩阵是酉矩阵：

设 $F_n$ 的列向量分别为 $\vec{f}_0 , \vec{f}_2 , \cdots , \vec{f}_{n - 1}$ ，即证 $\vec{f}_a^H \vec{f}_b = \left\{\begin{matrix} 0 , a \ne b \\ 1,a = b \end{matrix}\right.$

$\begin{aligned} \vec{f}_a^H \vec{f}_b & = \overline{(F_n)_{0 , a}} * (F_n)_{0 , b} + \overline{(F_n)_{1 , a}} * (F_n)_{1 , b} + \cdots + \overline{(F_n)_{n - 1 , a}} * (F_n)_{n - 1 , b} \\ & = w^{0(a + b)} + w^{a + b} + \cdots + w^{(n - 1)(a + b)} \end{aligned}$

$\color{OrangeRed}暂时不会证明$
傅里叶变换

当 $n = 4$ 时， $\dfrac{2 \pi}{n} = \dfrac{\pi}{2}$ ，所以 $w$ 的乘方落在实轴和虚轴上2，由此得到四阶傅里叶矩阵 $F_4 = \dfrac{1}{4} \begin{bmatrix} 1 & 1 & 1 & 1 \\ 1 & i & -1 & -i \\ 1 & -1 & 1 & -1 \\ 1 & -i & -1 & i \end{bmatrix}$

用 $F_4$ 左乘四维向量即为四点离散傅里叶变换（ $D FT$ ），用 $F_4^{-1}$ 左乘四维向量即为傅里叶逆变换
快速傅里叶变换

实际上可以将傅里叶矩阵分解为一系列“稀疏矩阵”，这些矩阵具有大量零元素，可以很方便地求逆及用于相乘

现在考虑 $F_{64}$ 与 $F_{32}$ 之间的联系，假设 $F_{32} , F_{64}$ 中的 $w$ 分别为 $w_{32} , w_{64}$ ，则 $w_{64}^2 = w_{32}$

先说结论： $F_{64} = \dfrac{1}{2} \begin{bmatrix} I & D \\ I & -D\end{bmatrix} \begin{bmatrix} F_{32} & O \\ O & F_{32}\end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & 0 & \cdots \\ 0 & 0 & 1 & 0 & \cdots \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & 1 & 0 & 0 & \cdots \\ 0 & 0 & 0 & 1 & \cdots \\ \vdots & \vdots & \vdots & \vdots & \vdots \end{bmatrix}$ ，其中 $\begin{bmatrix} 1 & 0 & 0 & \cdots & 0 \\ 0 & w_{} & 0 & \cdots & 0 \\ 0 & 0 & w_{64}^2 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & w_{64}^{31} \end{bmatrix}$

证明： 可以发现 $F_{64}$ 拆分出的第三个矩阵将用于进行傅里叶变换的向量的偶数位元素提到了前面而将奇数位元素放到了后面，然后拆分出的第二个矩阵对刚才得到的新向量中的前后两部分分别做一次 $32$ 阶傅里叶变换

对于新向量前半部分，第 $i$ 个元素在求 $32$ 阶傅里叶变换后的第 $j$ 行时乘上了 $w_{32}^{ji}$ ，而新向量前半部分的第 $i$ 个元素是原向量的第 $2 * i$ 个元素，这说明它在求 $64$ 阶傅里叶变换后的第 $j$ 行时应该乘上 $w_{64}^{2ji}$ ，刚好 $w_{32}^{ji} = w_{64}^{2ji}$ ，所以 $F_{64}$ 拆分出的第一个矩阵左半部分上方是单位向量，对于下方，新向量前半部分的第 $i$ 个元素在求 $64$ 阶傅里叶变换后的第 $32 + j$ 行时应乘上 $w_{64}^{2(32 + j)i} = w_{32}^{(32 + j)i} = w_{32}^{ji} w_{32}^{32i} = w_{32}^{ji} (-1)^i = w_{32}^{ji}$ ，所以左半部分下方也是单位矩阵

对于新向量后半部分，第 $i$ 个元素在求 $32$ 阶傅里叶变换后的第 $j$ 行时乘上了 $w_{32}^{ji}$ ，而在求 $64$ 阶傅里叶变换后的第 $j$ 行时应该乘上 $w_{64}^{j(2i + 1)}$ ，即 $w_{32}^{ji} * w_{64}^j$ ，由此得到 $D$ ，对于拆分出的第一个矩阵右半部分下方，新向量后半部分的第 $i$ 个元素在求 $64$ 阶傅里叶变换后的第 $32 + j$ 行时应乘上 $w_{64}^{2(32 + j)i} = w_{32}^{ji} (-1)^i = -w_{32}^{ji}$ ，所以右半部分下方是 $- D$

最后说明 $\dfrac{1}{2}$ ，因为前面进行 $32$ 阶傅里叶变换时只除以了 $32$ ，所以最后还要再除以 $2$ 才能达到除以 $64$

为了直观地说明，此处只证明了 $F_{64}$ 到 $F_{32}$ 的拆分，对于 $F_{2n}$ 到 $F_n$ 的拆分，将具体的数字换为字母后也可得证

直接进行 $64$ 阶傅里叶变换的时间复杂度是 $O(n^2)$ ，而拆分为三个矩阵后，第三个矩阵和原向量相乘时间复杂度为 $O (n)$ ，第二个矩阵和新向量相乘时间复杂度为 $O(\dfrac{n^2}{2})$ ，此时得到的向量和第一个矩阵相乘时间复杂度为 $O (n)$ ，总时间复杂度为 $(\dfrac{n}{2})^2 + n)$ ，当然这还没有结束，因为第二个矩阵的 $F_{32}$ 可以进行类似的拆分得到含有 $F_{16}$ 的三个矩阵，这样刚才求得的总时间复杂度进一步简化得到 $(\dfrac{n}{4})^2 + \dfrac{n}{2}) + n) = O(2^2 (\dfrac{n}{4})^2 + 2n)$ ，以此类推，一层层拆分下去，时间复杂度就会降为 $n\ log\ n)$ ，即 $O(n\ log\ n)$