OpenCV快速入门：图像形态学操作-Toy模板网

这篇具有很好参考价值的文章主要介绍了OpenCV快速入门：图像形态学操作。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

前言

图像形态学是一门强大而有趣的技术，它通过对图像进行形态学操作，使图像更适合后续处理步骤。在本文中，我们将深入探讨OpenCV中的图像形态学操作，快速入门这一关键领域。

OpenCV快速入门：图像形态学操作,OpenCV,opencv,人工智能,计算机视觉

一、图像形态学基础

1.1 背景介绍

图像形态学作为数字图像处理的一个分支，致力于通过形态学操作实现对图像特征的提取、噪音的去除以及目标的分割。这一领域的研究为计算机视觉、图像识别和医学图像处理等领域提供了强大的工具和方法。

1.2 像素距离

在图像处理中，像素距离是一项关键的概念，它涉及到图像中像素点之间的空间关系。理解像素距离对于各种图像分析任务非常重要。

1.2.1 什么是像素距离？

像素距离是指图像中两个像素点之间的距离或度量。这一概念在许多图像处理任务中都有广泛的应用，例如目标的距离测量、轮廓分析等。

1.2.2 常见的像素距离度量方法

请参考机器学习中常见的距离公式和相似度计算方法简介中的常见的距离公式相关内容

1.2.3 计算像素距离的代码实现

在OpenCV中，计算像素距离通常使用 cv2.distanceTransform 函数。这个函数可以计算图像中每个像素点到最近的零值像素的距离。

import cv2
import numpy as np

# 生成简单的二值化图像
image = np.zeros((300, 300), dtype=np.uint8)+150
cv2.rectangle(image, (50, 50), (250, 250), 0, -1)
cv2.circle(image, (200, 200), 50, 255, -1)

margin = np.zeros((300, 10), dtype=np.uint8)
# 计算像素距离
distance_transform = cv2.distanceTransform(image, cv2.DIST_L2, 3)
distance_transform = cv2.normalize(distance_transform, None, 255,0, cv2.NORM_MINMAX, cv2.CV_8UC1)

# 显示像素距离图像
cv2.imshow('Distance Transform', cv2.hconcat([image, margin, distance_transform]))
cv2.waitKey(0)
cv2.destroyAllWindows()

OpenCV快速入门：图像形态学操作,OpenCV,opencv,人工智能,计算机视觉

通过这样的计算，我们可以获得图像中每个像素点到最近的零值像素的距离，并在图像上进行可视化展示。

在图像处理中，像素距离是一项重要的概念，它为我们提供了衡量图像空间关系的有效工具。OpenCV中的 cv2.distanceTransform 函数使得计算像素距离变得简单而高效。在实际应用中，了解并熟练使用像素距离的概念，将有助于更好地理解和处理图像，为后续的图像形态学操作打下基础。

1.3 图像连通性

在图像处理中，图像连通性是一个关键概念，它描述了图像中像素点之间的连接关系。理解图像的连通性有助于分析和处理图像中的目标、区域及其结构。本节将深入讨论图像连通性的概念以及在OpenCV中的应用。

1.3.1 什么是图像连通性？

图像连通性是指图像中像素点之间的连接关系或连通关系。当两个像素点通过相邻的水平、垂直或对角线位置相连时，它们被认为是连通的。连通性的概念对于分析图像中的物体、区域或对象之间的连接关系至关重要。

1.3.2 连通类型

图像连通性可以根据连接像素点的方式分为不同类型，常见的包括：

4连通： 像素点通过水平和垂直方向相邻时被视为连通。

8连通： 像素点通过水平、垂直和对角线方向相邻时被视为连通。

D连通： 一种介于4连通和8连通之间的连通类型，通常指像素点通过水平、垂直和对角线方向的一部分相邻时被视为连通。

在实际应用中，选择适当的连通类型取决于图像中目标的形状和特性。

1.3.3 连通组件标记

在图像处理中，常常需要标记和识别图像中的不同连通组件，即图像中连通的区域。这个过程被称为连通组件标记。OpenCV提供了相关函数来执行这一任务，如 cv2.connectedComponents。

import cv2
import numpy as np

# 生成简单的二值化图像
image = np.zeros((300, 300), dtype=np.uint8)+150
cv2.rectangle(image, (50, 50), (150, 150), 255, -1)
cv2.rectangle(image, (50, 50), (250, 250), 0, -1)
cv2.circle(image, (150, 150), 50, 255, -1)

# 连通组件标记
num_labels, labels = cv2.connectedComponents(image)

# 共享的参数
shared_params = {
    "org": (10, 30),
    "fontFace": cv2.FONT_HERSHEY_SIMPLEX,
    "fontScale": 1,
    "thickness": 2,
    "color": 255,
    "lineType": cv2.LINE_AA,
}
shared_params2 = {
    "org": (10, 30),
    "fontFace": cv2.FONT_HERSHEY_SIMPLEX,
    "fontScale": 1,
    "thickness": 10,
    "color": 0,
    "lineType": cv2.LINE_AA,
}
# 添加文字
cv2.putText(image, "Original Image",**shared_params)

connected_image = cv2.hconcat([image])
for label in range(0, num_labels):
    component = np.zeros_like(image)
    component[labels == label] = 255
    cv2.putText(component, f'Component {label+1}', **shared_params2)
    cv2.putText(component, f'Component {label+1}', **shared_params)
    connected_image = cv2.hconcat([connected_image,component])

cv2.imshow('Connected Components', connected_image)
cv2.waitKey(0)
cv2.destroyAllWindows()

OpenCV快速入门：图像形态学操作,OpenCV,opencv,人工智能,计算机视觉

在这个例子中，我们生成了一个简单的二值化图像，并使用 cv2.connectedComponents 对图像进行连通组件标记。通过遍历标记结果，我们可以分别显示不同的连通组件，以便更好地理解图像中的连通性。

一些场景中需要实现图像的连通性检测并在原图中用框线标出，我们可以使用OpenCV的cv2.connectedComponentsWithStats来获取图像中的连通组件。然后，遍历每个连通组件，获取其边界框信息，并在原图中用绿色矩形标出。

import cv2
import numpy as np
import random

# 创建一个空白的图像
width, height = 500, 500
image = np.zeros((height, width, 3), dtype=np.uint8)

# 定义绘制椭圆的函数
def draw_random_ellipse(img):
    # 生成随机椭圆的参数
    center = (random.randint(0, width-1), random.randint(0, height-1))
    axes = (random.randint(10, 100), random.randint(10, 100))
    angle = random.randint(0, 360)
    color = (random.randint(0, 255), random.randint(0, 255), random.randint(0, 255))

    # 绘制椭圆
    cv2.ellipse(img, center, axes, angle, 0, 360, color, -1)

# 定义检查椭圆是否重叠的函数
def check_overlap(new_ellipse, existing_ellipses):
    for existing_ellipse in existing_ellipses:
        # 获取椭圆的掩码
        new_mask = np.zeros_like(image, dtype=np.uint8)
        existing_mask = np.zeros_like(image, dtype=np.uint8)
        cv2.ellipse(new_mask, new_ellipse[0], new_ellipse[1], new_ellipse[2], 0, 360, (255, 255, 255), -1)
        cv2.ellipse(existing_mask, existing_ellipse[0], existing_ellipse[1], existing_ellipse[2], 0, 360, (255, 255, 255), -1)

        # 检查是否有重叠的部分
        overlap = cv2.bitwise_and(new_mask, existing_mask)
        if np.sum(overlap) > 0:
            return True
    return False

# 生成不重叠的椭圆
num_ellipses = 10
ellipses = []
for _ in range(num_ellipses):
    while True:
        new_ellipse = (
            (random.randint(0, width-1), random.randint(0, height-1)),
            (random.randint(10, 100), random.randint(10, 100)),
            random.randint(0, 360),
            (random.randint(0, 255), random.randint(0, 255), random.randint(0, 255))
        )
        if not check_overlap(new_ellipse, ellipses):
            ellipses.append(new_ellipse)
            break

# 绘制不重叠的椭圆
for ellipse in ellipses:
    cv2.ellipse(image, ellipse[0], ellipse[1], ellipse[2], 0, 360, ellipse[3], -1)


# 将图像转换为灰度
gray_image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)

# 进行连通组件标记
_, labels, stats, centroids = cv2.connectedComponentsWithStats(gray_image)

# 获取连通组件的数量（排除背景）
num_labels = len(stats) - 1

# 遍历每个连通组件并在原图中用矩形标出
for i in range(1, num_labels + 1):
    x, y, w, h, _ = stats[i]
    cv2.rectangle(image, (x, y), (x + w, y + h), (0, 255, 0), 2)

# 显示图像
cv2.imshow("Connected Components", image)
cv2.waitKey(0)
cv2.destroyAllWindows()

一些运行效果图：

OpenCV快速入门：图像形态学操作,OpenCV,opencv,人工智能,计算机视觉

1.3.4 连通性在图像处理中的应用

对象计数： 通过连通性分析，可以对图像中的对象进行计数，例如图像中的颗粒或细胞。

区域分割： 连通性信息有助于对图像进行区域分割，使得图像中的不同部分能够被准确地提取和分析。

目标识别： 在计算机视觉领域，通过连通性可以识别和跟踪图像中的目标，如人脸、车辆等。

图像连通性是图像处理中的一个基础而重要的概念，它为我们提供了理解和分析图像结构的有效工具。在OpenCV中，相关函数的支持使得连通性的计算变得更加便捷。通过深入理解图像连通性，我们能够更好地处理图像数据，为后续的图像分析和处理工作打下坚实的基础。

1.4 结构元素

在图像形态学操作中，结构元素是一种关键的概念，它为执行膨胀、腐蚀等操作提供了模板。本节将深入探讨结构元素的概念以及不同类型的结构元素在OpenCV中的应用。

1.4.1 什么是结构元素？

结构元素是一种小的、可以在图像上滑动的模板，用于定义形态学操作的形状和大小。它是膨胀、腐蚀、开运算和闭运算等操作的基础。

1.4.2 结构元素的类型

在OpenCV中，常见的结构元素有三种类型：矩形结构元素、圆形结构元素和十字形结构元素。

1.4.2.1 矩形结构元素

矩形结构元素是一种基本的结构元素，其形状为矩形。在图像处理中，矩形结构元素通常用于执行基本的膨胀和腐蚀操作。它的定义可以通过OpenCV的 cv2.getStructuringElement 函数实现：

import cv2
# 定义矩形结构元素
rectangle_kernel = cv2.getStructuringElement(cv2.MORPH_RECT, (5, 5))
# 打印矩形结构元素
print(rectangle_kernel)

运行结果

[[1 1 1 1 1]
 [1 1 1 1 1]
 [1 1 1 1 1]
 [1 1 1 1 1]
 [1 1 1 1 1]]

1.4.2.2 圆形结构元素

圆形结构元素的形状为圆形，适用于处理需要考虑像素点周围更广泛范围的情况。同样，通过 cv2.getStructuringElement 函数可以轻松地创建圆形结构元素：

import cv2
# 定义圆形结构元素
circle_kernel = cv2.getStructuringElement(cv2.MORPH_ELLIPSE, (5, 5))
# 打印圆形结构元
print(circle_kernel)

[[0 0 1 0 0]
 [1 1 1 1 1]
 [1 1 1 1 1]
 [1 1 1 1 1]
 [0 0 1 0 0]]

1.4.2.3 十字形结构元素

十字形结构元素是一种与十字交叉形状相似的结构元素，适用于强调对角方向的形态学操作。创建十字形结构元素的方法如下：

import cv2
# 定义十字形结构元素
cross_kernel = cv2.getStructuringElement(cv2.MORPH_CROSS, (5, 5))
# 打印十字形结构元素
print(cross_kernel)

[[0 0 1 0 0]
 [0 0 1 0 0]
 [1 1 1 1 1]
 [0 0 1 0 0]
 [0 0 1 0 0]]

1.4.2.4 自定义结构元素

有时，我们可能需要根据具体任务定义自己的结构元素，例如使用特定的形状或大小。可以直接创建一个NumPy数组作为自定义的结构元素，然后传递给形态学操作的函数：

import cv2
import numpy as np

# 定义自定义结构元素
custom_kernel = np.array([[0, 1, 0],
                          [1, 1, 1],
                          [0, 1, 0]], dtype=np.uint8)

# 显示自定义结构元素
cv2.imshow('Custom Kernel', custom_kernel * 255)
cv2.waitKey(0)
cv2.destroyAllWindows()

二、膨胀与腐蚀

在图像处理中，膨胀与腐蚀是两种常用的图像形态学操作，它们分别用于扩大和减小图像中物体的区域，是图像处理中不可或缺的基础操作。

2.1 膨胀操作

膨胀是一种通过增加图像中物体的像素点来扩大物体的面积的操作。膨胀操作的核心思想是使用一个结构元素（通常是矩形、圆形或十字形），在图像上滑动，将结构元素的中心与图像中的像素匹配。如果结构元素的中心与图像中的像素点匹配，那么就将结构元素覆盖的区域置为白色（255）。

2.1.1 膨胀操作的原理

膨胀操作的数学表达可以用以下形式表示：

$\oplus B)(x, y) = \bigcup_{(i, j) \in B} A(x+i, y+j)$

其中， $A$ 是输入图像， $B$ 是结构元素， $\oplus B)(x, y)$ 表示在图像 $A$ 上对结构元素 $B$ 进行膨胀操作的结果。在膨胀操作中，对于结构元素 $B$ 中的每一个元素 $(i, j)$ ，将图像 $A$ 中与之对应的像素置为白色。最终的膨胀结果即为所有置为白色的像素的并集。

2.1.2 膨胀操作的应用

膨胀操作在图像处理中有多种应用场景：

连接物体： 将相邻的物体像素连接在一起，形成更大的物体。

填充小洞： 用于填充图像中小的空洞，使物体更加完整。

增加物体面积： 通过扩展物体的边界，增加物体的面积。

2.1.3 膨胀操作的代码示例

在OpenCV中，可以使用 cv2.dilate 函数进行膨胀操作。以下是一个简单的Python代码示例：
OpenCV快速入门：图像形态学操作,OpenCV,opencv,人工智能,计算机视觉
random_ellipse1.jpg

import cv2
import numpy as np

# 读取图像
image = cv2.imread('random_ellipse1.jpg')
# 定义矩形结构元素
rectangle_kernel = cv2.getStructuringElement(cv2.MORPH_RECT, (5, 5))
# 膨胀操作
dilated_image = cv2.dilate(image, rectangle_kernel, iterations=1)


# 图像连通性
def draw_connected_image(src_img):
    # 将图像转换为灰度
    gray_image = cv2.cvtColor(src_img, cv2.COLOR_BGR2GRAY)
    # 二值化
    threshold_value = 20
    _, binary_image = cv2.threshold(gray_image, threshold_value, 255, cv2.THRESH_BINARY)
    # 进行连通组件标记
    _, labels, stats, centroids = cv2.connectedComponentsWithStats(binary_image)
    # 获取连通组件的数量（排除背景）
    num_labels = len(stats) - 1
    # 遍历每个连通组件并在原图中用矩形标出
    for i in range(1, num_labels + 1):
        x, y, w, h, _ = stats[i]
        cv2.rectangle(src_img, (x, y), (x + w, y + h), (0, 255, 0), 2)
    return src_img


# 共享的参数
shared_params = {
    "org": (10, 30),
    "fontFace": cv2.FONT_HERSHEY_SIMPLEX,
    "fontScale": 1,
    "thickness": 2,
    "color": (0, 255, 0),
    "lineType": cv2.LINE_AA,
}
# 增加黑框
shared_params2 = {
    "org": (10, 30),
    "fontFace": cv2.FONT_HERSHEY_SIMPLEX,
    "fontScale": 1,
    "thickness": 10,
    "color": (0, 0, 0),
    "lineType": cv2.LINE_AA,
}
# 添加文字
image_txt = cv2.putText(image.copy(), "Original Image", **shared_params2)
image_txt = cv2.putText(image_txt, "Original Image", **shared_params)
dilated_image_txt = cv2.putText(dilated_image.copy(), "Dilated Image", **shared_params2)
dilated_image_txt = cv2.putText(dilated_image_txt, "Dilated Image", **shared_params)

# 显示原始图像和膨胀结果
cv2.imshow('Dilated Image', cv2.vconcat([
    cv2.hconcat([image_txt, draw_connected_image(image.copy())]),
    np.zeros((10, image.shape[1] * 2, 3), dtype=np.uint8) + 255,
    cv2.hconcat([dilated_image_txt, draw_connected_image(dilated_image.copy())])
]))
cv2.waitKey(0)
cv2.destroyAllWindows()

OpenCV快速入门：图像形态学操作,OpenCV,opencv,人工智能,计算机视觉

我们可以看到，经过膨胀操作之后，有两处原本不相连的椭圆变为相连的情况。

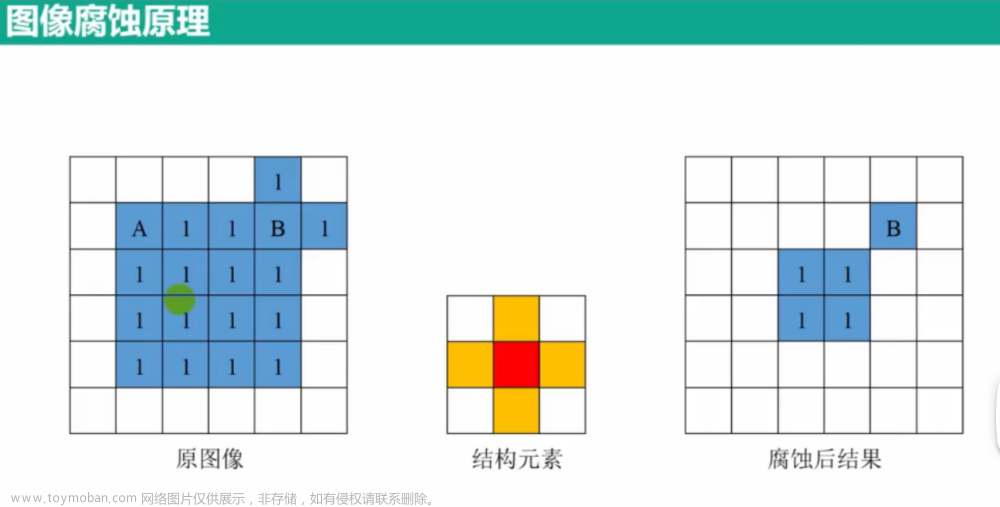
2.2 腐蚀操作

与膨胀相反，腐蚀是一种通过减少物体的像素点来减小物体的面积的操作。腐蚀操作同样使用一个结构元素，当结构元素的中心与图像中的像素匹配时，仅当结构元素的所有像素都与图像中的像素匹配时，才将中心像素置为白色（255），否则置为黑色（0）。

2.2.1腐蚀操作的原理

腐蚀操作的数学表达可以用以下形式表示：

$\ominus B)(x, y) = \bigcap_{(i, j) \in B} A(x+i, y+j)$

其中， $A$ 是输入图像， $B$ 是结构元素， $\ominus B)(x, y)$ 表示在图像 $A$ 上对结构元素 $B$ 进行腐蚀操作的结果。在腐蚀操作中，对于结构元素 $B$ 中的每一个元素 $(i, j)$ ，将图像 $A$ 中与之对应的像素与结构元素的对应像素进行比较。如果结构元素覆盖的区域内所有像素都为白色，那么中心像素置为白色，否则置为黑色。最终的腐蚀结果即为所有中心像素为白色的区域的交集。

2.2.2腐蚀操作的应用

腐蚀操作在图像处理中有多种应用场景：

去除小物体： 用于去除图像中较小的物体或细小的细节。

平滑物体边界： 通过减小物体的边界，使其更加平滑。

分离连接的物体： 将相连的物体分离开，使其更容易识别和分析。

2.2.3腐蚀操作的代码示例

在OpenCV中，可以使用 cv2.erode 函数进行腐蚀操作。以下是一个简单的Python代码示例：
OpenCV快速入门：图像形态学操作,OpenCV,opencv,人工智能,计算机视觉
random_ellipse2.jpg

import cv2
import numpy as np

# 读取图像
image = cv2.imread('random_ellipse2.jpg')
# 定义矩形结构元素
rectangle_kernel = cv2.getStructuringElement(cv2.MORPH_RECT, (5, 5))
# 腐蚀操作
eroded_image = cv2.erode(image, rectangle_kernel, iterations=1)


# 图像连通性
def draw_connected_image(src_img):
    # 将图像转换为灰度
    gray_image = cv2.cvtColor(src_img, cv2.COLOR_BGR2GRAY)
    # 二值化
    threshold_value = 20
    _, binary_image = cv2.threshold(gray_image, threshold_value, 255, cv2.THRESH_BINARY)
    # 进行连通组件标记
    _, labels, stats, centroids = cv2.connectedComponentsWithStats(binary_image)
    # 获取连通组件的数量（排除背景）
    num_labels = len(stats) - 1
    # 遍历每个连通组件并在原图中用矩形标出
    for i in range(1, num_labels + 1):
        x, y, w, h, _ = stats[i]
        cv2.rectangle(src_img, (x, y), (x + w, y + h), (0, 255, 0), 2)
    return src_img


# 共享的参数
shared_params = {
    "org": (10, 30),
    "fontFace": cv2.FONT_HERSHEY_SIMPLEX,
    "fontScale": 1,
    "thickness": 2,
    "color": (0, 255, 0),
    "lineType": cv2.LINE_AA,
}
# 增加黑框
shared_params2 = {
    "org": (10, 30),
    "fontFace": cv2.FONT_HERSHEY_SIMPLEX,
    "fontScale": 1,
    "thickness": 10,
    "color": (0, 0, 0),
    "lineType": cv2.LINE_AA,
}
# 添加文字
image_txt = cv2.putText(image.copy(), "Original Image", **shared_params2)
image_txt = cv2.putText(image_txt, "Original Image", **shared_params)
eroded_image_txt = cv2.putText(eroded_image.copy(), "Eroded Image", **shared_params2)
eroded_image_txt = cv2.putText(eroded_image_txt, "Eroded Image", **shared_params)

# 显示原始图像和腐蚀结果
cv2.imshow('Eroded Image', cv2.vconcat([
    cv2.hconcat([image_txt, draw_connected_image(image.copy())]),
    np.zeros((10, image.shape[1] * 2, 3), dtype=np.uint8) + 255,
    cv2.hconcat([eroded_image_txt, draw_connected_image(eroded_image.copy())])
]))
cv2.waitKey(0)
cv2.destroyAllWindows()

OpenCV快速入门：图像形态学操作,OpenCV,opencv,人工智能,计算机视觉

我们可以看到，有一处原本相连的椭圆，经过腐蚀操作后变为了不相连的两个椭圆。

三、开运算与闭运算

3.1 开运算

开运算原理是先对图像进行腐蚀操作，然后再对腐蚀结果进行膨胀操作。开运算通常用于去除图像中的小噪点、平滑物体边界，并保留物体的整体形状。在数学表达上，开运算可以表示为：

$\text{Opening}(A) = (A \ominus B) \oplus B$

其中， $A$ 是输入图像， $B$ 是结构元素， $\ominus$ 表示腐蚀操作， $\oplus$ 表示膨胀操作， $\text{Opening}(A)$ 表示对图像 $A$ 进行开运算的结果。

3.1.1 开运算的应用

开运算主要应用于以下场景：

去除小噪点： 通过先腐蚀操作，可以去除图像中小于结构元素的噪点。

平滑物体边界： 腐蚀操作会使物体边界向内收缩，而膨胀操作会使其向外扩张，从而平滑物体的边界。

保留整体形状： 开运算可以保留物体的整体形状，有助于提取物体的主要结构。

3.1.2 开运算的代码示例

在OpenCV中，可以使用 cv2.morphologyEx 函数进行开运算。以下是一个简单的Python代码示例：

import cv2
import numpy as np

# 生成一个黑色背景的图像
image_size = (300, 300)
image = np.zeros(image_size, dtype=np.uint8)

# 在图像中添加一些形状
cv2.circle(image, (50, 50), 20, 255, -1)
cv2.circle(image, (150, 150), 30, 255, -1)
cv2.rectangle(image, (200, 100), (250, 200), 255, -1)
cv2.ellipse(image, (100, 200), (40, 20), 30, 0, 360, 255, -1)
# 绘制白色椭圆弧
cv2.ellipse(image, (210, 210), (100, 50), 0, 180, 270, 255, 2)

# 定义矩形结构元素
rectangle_kernel = cv2.getStructuringElement(cv2.MORPH_RECT, (5, 5))
# 开运算操作
opening_result = cv2.morphologyEx(image, cv2.MORPH_OPEN, rectangle_kernel)


# 图像连通性
def draw_connected_image(src_img):
    # 二值化
    threshold_value = 20
    _, binary_image = cv2.threshold(src_img, threshold_value, 255, cv2.THRESH_BINARY)
    # 进行连通组件标记
    _, labels, stats, centroids = cv2.connectedComponentsWithStats(binary_image)
    # 获取连通组件的数量（排除背景）
    num_labels = len(stats) - 1
    # 遍历每个连通组件并在原图中用矩形标出
    for i in range(1, num_labels + 1):
        x, y, w, h, _ = stats[i]
        cv2.rectangle(src_img, (x, y), (x + w, y + h), 127, 2)
    return src_img


# 共享的参数
shared_params = {
    "org": (10, 30),
    "fontFace": cv2.FONT_HERSHEY_SIMPLEX,
    "fontScale": 1,
    "thickness": 2,
    "color": 255,
    "lineType": cv2.LINE_AA,
}
# 增加黑框
shared_params2 = {
    "org": (10, 30),
    "fontFace": cv2.FONT_HERSHEY_SIMPLEX,
    "fontScale": 1,
    "thickness": 10,
    "color": 0,
    "lineType": cv2.LINE_AA,
}
# 添加文字
image_txt = cv2.putText(image.copy(), "Original Image", **shared_params2)
image_txt = cv2.putText(image_txt, "Original Image", **shared_params)
opening_result_txt = cv2.putText(opening_result.copy(), "Opening Result", **shared_params2)
opening_result_txt = cv2.putText(opening_result_txt, "Opening Result", **shared_params)

# 显示原始图像和开运算结果
cv2.imshow('Opening Result', cv2.vconcat([
    cv2.hconcat([image_txt, draw_connected_image(image.copy())]),
    np.zeros((10, image.shape[1] * 2), dtype=np.uint8) + 255,
    cv2.hconcat([opening_result_txt, draw_connected_image(opening_result.copy())])
]))
cv2.waitKey(0)
cv2.destroyAllWindows()

OpenCV快速入门：图像形态学操作,OpenCV,opencv,人工智能,计算机视觉
通过理解开运算的原理和应用，我们可以更好地利用这一操作来去除图像中的噪点、平滑物体边界，从而为后续的图像分析和处理提供更清晰、更准确的数据。在实际应用中，可以根据具体情况选择不同的结构元素和迭代次数，以达到最佳的开运算效果。

3.2 闭运算

闭运算原理是先对图像进行膨胀操作，然后再对膨胀结果进行腐蚀操作。闭运算通常用于连接物体间的小孔、填充小的间隙，并保持物体的整体形状。在数学表达上，闭运算可以表示为：

$\text{Closing}(A) = (A \oplus B) \ominus B$

其中， $A$ 是输入图像， $B$ 是结构元素， $\oplus$ 表示膨胀操作， $\ominus$ 表示腐蚀操作， $\text{Closing}(A)$ 表示对图像 $A$ 进行闭运算的结果。

3.2.1 闭运算的应用

闭运算主要应用于以下场景：

连接物体间的小孔： 通过先膨胀操作，可以连接物体之间的小孔，使其更加连续。

填充小的间隙： 膨胀操作会使物体边界向外扩张，腐蚀操作会使其向内收缩，从而填充物体间的小间隙。

保持整体形状： 闭运算可以保持物体的整体形状，有助于提取物体的主要结构。

3.2.2 闭运算的代码示例

在OpenCV中，可以使用 cv2.morphologyEx 函数进行闭运算。以下是一个简单的Python代码示例：

import cv2
import numpy as np

# 生成一个黑色背景的图像
image_size = (300, 300)
image = np.zeros(image_size, dtype=np.uint8)

# 在图像中添加一些形状
cv2.circle(image, (50, 50), 20, 255, -1)
cv2.circle(image, (150, 150), 30, 255, -1)
cv2.rectangle(image, (200, 100), (250, 200), 255, -1)
cv2.ellipse(image, (100, 200), (40, 20), 30, 0, 360, 255, -1)
# 绘制白色椭圆弧
cv2.ellipse(image, (223, 223), (100, 50), 0, 210, 253, 255, 2)

# 定义矩形结构元素
rectangle_kernel = cv2.getStructuringElement(cv2.MORPH_RECT, (5, 5))
# 闭运算操作
closing_result = cv2.morphologyEx(image, cv2.MORPH_CLOSE, rectangle_kernel)


# 图像连通性
def draw_connected_image(src_img):
    # 二值化
    threshold_value = 20
    _, binary_image = cv2.threshold(src_img, threshold_value, 255, cv2.THRESH_BINARY)
    # 进行连通组件标记
    _, labels, stats, centroids = cv2.connectedComponentsWithStats(binary_image)
    # 获取连通组件的数量（排除背景）
    num_labels = len(stats) - 1
    # 遍历每个连通组件并在原图中用矩形标出
    for i in range(1, num_labels + 1):
        x, y, w, h, _ = stats[i]
        cv2.rectangle(src_img, (x, y), (x + w, y + h), 127, 2)
    return src_img


# 共享的参数
shared_params = {
    "org": (10, 30),
    "fontFace": cv2.FONT_HERSHEY_SIMPLEX,
    "fontScale": 1,
    "thickness": 2,
    "color": 255,
    "lineType": cv2.LINE_AA,
}
# 增加黑框
shared_params2 = {
    "org": (10, 30),
    "fontFace": cv2.FONT_HERSHEY_SIMPLEX,
    "fontScale": 1,
    "thickness": 10,
    "color": 0,
    "lineType": cv2.LINE_AA,
}
# 添加文字
image_txt = cv2.putText(image.copy(), "Original Image", **shared_params2)
image_txt = cv2.putText(image_txt, "Original Image", **shared_params)
closing_result_txt = cv2.putText(closing_result.copy(), "Closing Result", **shared_params2)
closing_result_txt = cv2.putText(closing_result_txt, "Closing Result", **shared_params)

# 显示原始图像和闭运算结果
cv2.imshow('Closing Result', cv2.vconcat([
    cv2.hconcat([image_txt, draw_connected_image(image.copy())]),
    np.zeros((10, image.shape[1] * 2), dtype=np.uint8) + 255,
    cv2.hconcat([closing_result_txt, draw_connected_image(closing_result.copy())])
]))
cv2.waitKey(0)
cv2.destroyAllWindows()

OpenCV快速入门：图像形态学操作,OpenCV,opencv,人工智能,计算机视觉
通过理解闭运算的原理和应用，我们可以更好地利用这一操作来连接物体间的小孔、填充小的间隙，从而使图像更加连续、完整。在实际应用中，可以根据具体情况选择不同的结构元素和迭代次数，以达到最佳的闭运算效果。

四、黑帽运算与礼帽运算

4.1 黑帽运算

黑帽运算原理是先对图像进行闭运算，然后将闭运算的结果与原始图像相减。黑帽运算主要用于强调图像中的小细节、小物体或者图像中的局部区域。在数学表达上，黑帽运算可以表示为：

$\text{BlackHat}(A) = A - (A \oplus B)$

其中， $A$ 是输入图像， $B$ 是结构元素， $\oplus$ 表示膨胀操作。黑帽运算的结果即为原始图像减去闭运算的结果。

4.1.1 黑帽运算的应用

黑帽运算主要应用于以下场景：

强调小细节： 通过突出图像中的小细节，使其更加突出。

增强小物体： 用于增强图像中的小物体，使其更容易被检测和识别。

局部区域处理： 对图像中的局部区域进行强调，有助于分析局部特征。

4.1.2 黑帽运算的代码示例

以下是一个简单的Python代码示例：

import cv2
import numpy as np

# 生成一个黑色背景的图像
image_size = (300, 300)
image = np.zeros(image_size, dtype=np.uint8)

# 在图像中添加一些形状
cv2.circle(image, (50, 50), 20, 255, -1)
cv2.circle(image, (150, 150), 30, 255, -1)
cv2.rectangle(image, (200, 100), (250, 200), 255, -1)
cv2.ellipse(image, (100, 200), (40, 20), 30, 0, 360, 255, -1)
# 绘制白色椭圆弧
cv2.ellipse(image, (223, 223), (100, 50), 0, 210, 253, 255, 2)

# 定义矩形结构元素
rectangle_kernel = cv2.getStructuringElement(cv2.MORPH_RECT, (5, 5))
# 黑帽运算
blackhat_result = cv2.morphologyEx(image, cv2.MORPH_BLACKHAT, rectangle_kernel)

# 共享的参数
shared_params = {
    "org": (10, 30),
    "fontFace": cv2.FONT_HERSHEY_SIMPLEX,
    "fontScale": 1,
    "thickness": 2,
    "color": 255,
    "lineType": cv2.LINE_AA,
}
# 增加黑框
shared_params2 = {
    "org": (10, 30),
    "fontFace": cv2.FONT_HERSHEY_SIMPLEX,
    "fontScale": 1,
    "thickness": 10,
    "color": 0,
    "lineType": cv2.LINE_AA,
}
# 添加文字
image_txt = cv2.putText(image.copy(), "Original Image", **shared_params2)
image_txt = cv2.putText(image_txt, "Original Image", **shared_params)
blackhat_result_txt = cv2.putText(blackhat_result.copy(), "BlackHat Result", **shared_params2)
blackhat_result_txt = cv2.putText(blackhat_result_txt, "BlackHat Result", **shared_params)

# 显示原始图像和黑帽运算结果
cv2.imshow('BlackHat Result', cv2.hconcat(
    [image_txt,
     np.zeros((image.shape[0], 10), dtype=np.uint8) + 255,
     blackhat_result_txt]))
cv2.waitKey(0)
cv2.destroyAllWindows()

OpenCV快速入门：图像形态学操作,OpenCV,opencv,人工智能,计算机视觉

4.2 礼帽运算

礼帽运算原理是先对图像进行开运算，然后将开运算的结果与原始图像相减。礼帽运算主要用于强调图像中的大细节、大物体或者图像中的全局区域。在数学表达上，礼帽运算可以表示为：

$\text{TopHat}(A) = (A \oplus B) - A$

其中， $A$ 是输入图像， $B$ 是结构元素， $\oplus$ 表示膨胀操作。礼帽运算的结果即为开运算的结果减去原始图像。

4.2.1 礼帽运算的应用

礼帽运算主要应用于以下场景：

强调大细节： 通过突出图像中的大细节，使其更加显著。

增强大物体： 用于增强图像中的大物体，使其更容易被检测和识别。

全局区域处理： 对图像中的全局区域进行强调，有助于分析整体特征。

4.2.2 礼帽运算的代码示例

以下是一个简单的Python代码示例：

import cv2
import numpy as np

# 生成一个黑色背景的图像
image_size = (300, 300)
image = np.zeros(image_size, dtype=np.uint8)

# 在图像中添加一些形状
cv2.circle(image, (50, 50), 20, 255, -1)
cv2.circle(image, (150, 150), 30, 255, -1)
cv2.rectangle(image, (200, 100), (250, 200), 255, -1)
cv2.ellipse(image, (100, 200), (40, 20), 30, 0, 360, 255, -1)
# 绘制白色椭圆弧
cv2.ellipse(image, (223, 223), (100, 50), 0, 210, 253, 255, 2)

# 定义矩形结构元素
rectangle_kernel = cv2.getStructuringElement(cv2.MORPH_RECT, (5, 5))
# 礼帽运算
tophat_result = cv2.morphologyEx(image, cv2.MORPH_TOPHAT, rectangle_kernel)

# 共享的参数
shared_params = {
    "org": (10, 30),
    "fontFace": cv2.FONT_HERSHEY_SIMPLEX,
    "fontScale": 1,
    "thickness": 2,
    "color": 255,
    "lineType": cv2.LINE_AA,
}
# 增加黑框
shared_params2 = {
    "org": (10, 30),
    "fontFace": cv2.FONT_HERSHEY_SIMPLEX,
    "fontScale": 1,
    "thickness": 10,
    "color": 0,
    "lineType": cv2.LINE_AA,
}
# 添加文字
image_txt = cv2.putText(image.copy(), "Original Image", **shared_params2)
image_txt = cv2.putText(image_txt, "Original Image", **shared_params)
tophat_result_txt = cv2.putText(tophat_result.copy(), "TopHat Result", **shared_params2)
tophat_result_txt = cv2.putText(tophat_result_txt, "TopHat Result", **shared_params)

# 显示原始图像和礼帽运算结果
cv2.imshow('TopHat Result', cv2.hconcat(
    [image_txt,
     np.zeros((image.shape[0], 10), dtype=np.uint8) + 255,
     tophat_result_txt]))
cv2.waitKey(0)
cv2.destroyAllWindows()

OpenCV快速入门：图像形态学操作,OpenCV,opencv,人工智能,计算机视觉

通过理解黑帽运算和礼帽运算的原理和应用，我们可以更好地运用这两种操作来强调图像中的细节，实现更有针对性的图像处理效果。在实际应用中，可以根据具体情况选择不同的结构元素和运算类型，以达到最佳的效果。

五、击中与击不中

5.1 击中运算

击中运算用于检测图像中与给定模板相匹配的区域。在击中运算中，模板（结构元素）被应用于输入图像，只有当模板的所有像素与图像中对应位置的像素匹配时，才将中心像素置为白色（255），否则置为黑色（0）。数学表达上，击中运算可以表示为：

$\odot B)(x, y) = \begin{cases} 255 & \text{if } A(x+i, y+j) = B(i, j) \text{ for all } (i, j) \in B \\ 0 & \text{otherwise} \end{cases}$

其中， $A$ 是输入图像， $B$ 是结构元素， $\odot B)(x, y)$ 表示在图像 $A$ 上对结构元素 $B$ 进行击中运算的结果。

5.2 击不中运算

击不中运算是击中运算的补操作，用于检测图像中与给定模板不匹配的区域。在击不中运算中，模板（结构元素）被应用于输入图像，只有当模板的所有像素与图像中对应位置的像素不匹配时，才将中心像素置为白色（255），否则置为黑色（0）。数学表达上，击不中运算可以表示为：

$\oslash B)(x, y) = \begin{cases} 255 & \text{if } A(x+i, y+j) \neq B(i, j) \text{ for all } (i, j) \in B \\ 0 & \text{otherwise} \end{cases}$

其中， $A$ 是输入图像， $B$ 是结构元素， $\oslash B)(x, y)$ 表示在图像 $A$ 上对结构元素 $B$ 进行击不中运算的结果。

5.3 击中与击不中运算的应用

目标检测： 击中运算可用于检测图像中是否存在特定形状的目标。

形态学骨架提取： 击中运算与击不中运算在形态学骨架提取中有广泛应用。

图像分割： 运算可用于分割图像中的不同区域。

5.4 击中与击不中的代码示例

在OpenCV中，可以使用 cv2.morphologyEx 函数进行击中与击不中运算。以下是一个简单的Python代码示例：

import cv2
import numpy as np

# 生成一个黑色背景的图像
image_size = (300, 300)
image = np.zeros(image_size, dtype=np.uint8)

# 在图像中添加一些形状
cv2.circle(image, (50, 50), 20, 255, -1)
cv2.circle(image, (150, 150), 30, 255, -1)
cv2.rectangle(image, (200, 100), (250, 200), 255, -1)
cv2.ellipse(image, (100, 200), (40, 20), 30, 0, 360, 255, -1)
# 绘制白色椭圆弧
cv2.ellipse(image, (223, 223), (100, 50), 0, 210, 253, 255, 2)
# 盐噪声
pepper_noise = np.random.rand(*image.shape) < 0.5
image[pepper_noise] = 0

# 定义结构元素（内核）
kernel = np.array([[1, 0, 1],
                   [0, -1, 0],
                   [1, 0, 1]], dtype=np.int8)

# 击中运算
hitmiss_hit_result = cv2.morphologyEx(image.copy(), cv2.MORPH_HITMISS, kernel)

# 击不中运算
hitmiss_miss_result = cv2.morphologyEx(image, cv2.MORPH_HITMISS, cv2.bitwise_not(kernel))

# 显示原始图像、击中运算结果和击不中运算结果
cv2.imshow('Hit and Miss Result', cv2.hconcat([image, hitmiss_hit_result, hitmiss_miss_result]))
cv2.waitKey(0)
cv2.destroyAllWindows()

OpenCV快速入门：图像形态学操作,OpenCV,opencv,人工智能,计算机视觉
在形态学操作中，结构元素是一个小的二进制矩阵（或核），它定义了要在图像上应用的操作的形状。结构元素中的元素值通常是0和1，其中1表示结构元素的一部分，0表示不是结构元素的一部分。负数通常用于表示不考虑的区域。

在形态学击中和击不中操作中，结构元素是由1、0和-1组成的。具体含义如下：

1：表示目标的一部分（白色区域）。

0：表示不考虑的区域。

-1：表示背景的一部分（黑色区域）。

在先前的代码示例中，kernel_hit和kernel_miss中的1、0和-1的分布被设计为符合形态学击中和击不中的操作。这是为了确保在目标被击中时（kernel_hit），结构元素的白色部分与目标的白色部分重合，而在目标未被击中时（kernel_miss），结构元素的白色部分与目标的黑色背景部分重合。

这种表示方式可以根据具体的问题和需求进行调整，以确保形态学操作能够正确地捕捉目标的特定形状。

六、细化与粗化

6.1 细化操作

细化是一种形态学操作，用于减小二值图像中物体的宽度，使其更接近于图像中的中轴线。细化操作通过迭代地击中运算和击不中运算，逐渐减小物体的宽度。细化的数学表达可以表示为：

$\otimes B) = A - (A \odot B)$

其中， $A$ 是输入图像， $B$ 是结构元素， $\otimes$ 表示细化操作， $\odot$ 表示击中运算。细化操作的结果即为原始图像减去击中运算的结果。

6.2 粗化操作

粗化是细化操作的补操作，用于增加二值图像中物体的宽度，使其更接近于图像中的中轴线。粗化操作通过迭代地击中运算和击不中运算，逐渐增加物体的宽度。粗化的数学表达可以表示为：

$\odot B) \cup A$

其中， $A$ 是输入图像， $B$ 是结构元素， $\odot$ 表示击中运算。粗化操作的结果即为击中运算的结果与原始图像的并集。

6.3 细化与粗化操作的应用

骨架提取： 细化操作可用于提取图像中物体的骨架。

字符识别： 在字符识别中，细化可以帮助识别字符的主要形状。

图像分析： 细化和粗化操作可用于图像分析中的特征提取。

6.4 细化与粗化的代码示例

在OpenCV中，可以使用 cv2.morphologyEx 函数进行细化和粗化操作。以下是一个简单的Python代码示例：

import cv2
import numpy as np

# 生成一个黑色背景的图像
image_size = (300, 300)
image = np.zeros(image_size, dtype=np.uint8)

# 在图像中添加一些形状
cv2.circle(image, (50, 50), 20, 255, -1)
cv2.circle(image, (150, 150), 30, 255, -1)
cv2.rectangle(image, (200, 100), (250, 200), 255, -1)
cv2.ellipse(image, (100, 200), (40, 20), 30, 0, 360, 255, -1)
# 绘制白色椭圆弧
cv2.ellipse(image, (223, 223), (100, 50), 0, 210, 253, 255, 2)

# 执行细化操作
thin = cv2.ximgproc.thinning(image, thinningType=cv2.ximgproc.THINNING_GUOHALL)

# 执行粗化操作
# 创建形态学操作的结构元素
kernel = np.ones((3, 3), np.uint8)

# 使用形态学操作执行粗化
thick = cv2.dilate(image, kernel, iterations=1)

# 显示原始图像、细化操作结果和粗化操作结果
cv2.imshow('Thin and Thick Result', cv2.hconcat([image, thin, thick]))
cv2.waitKey(0)
cv2.destroyAllWindows()

OpenCV快速入门：图像形态学操作,OpenCV,opencv,人工智能,计算机视觉

通过理解细化与粗化操作的原理和应用，我们可以更好地运用这两种操作来实现骨架提取、字符识别等图像处理任务。在实际应用中，可以根据具体情况选择不同的结构元素和迭代次数，以达到最佳的细化或粗化效果。

总结

在本文中，我们介绍了图像形态学的基础知识和操作。首先，通过背景介绍，我们了解到图像形态学在图像处理中的重要性。接着，讨论了像素距离的概念及其度量方法，并提供了计算像素距离的代码实现。图像连通性作为关键概念，我们详细介绍了其定义、不同的连通类型以及在图像处理中的应用。

结构元素作为形态学操作的基础，我们介绍了不同类型的结构元素，并展示了如何自定义结构元素。膨胀、腐蚀、开运算、闭运算、黑帽运算和礼帽运算等操作被详细解释，并提供了相应的代码示例。最后，我们了解了击中与击不中、细化与粗化操作及其在图像处理中的应用，并展示了相应的代码示例。

通过本文的学习，我们对图像形态学的原理和实际应用有基本的理解，能够灵活运用这些操作解决实际图像处理问题。形态学操作在计算机视觉、图像识别等领域有着广泛的应用，为图像处理提供了强大的工具和技术。文章来源地址https://www.toymoban.com/news/detail-753710.html

到了这里，关于OpenCV快速入门：图像形态学操作的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！