【数据结构与算法】分别以邻接矩阵和邻接表作为存储结构实现以下操作：1.增加一个新顶点v、2.删除顶点v及其相关的边、3.增加一条边＜v，w＞、4.删除一条边＜v，w＞-Toy模板网

这篇具有很好参考价值的文章主要介绍了【数据结构与算法】分别以邻接矩阵和邻接表作为存储结构实现以下操作：1.增加一个新顶点v、2.删除顶点v及其相关的边、3.增加一条边＜v，w＞、4.删除一条边＜v，w＞。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

题目

Qestion: 分别以邻接矩阵和邻接表作为存储结构，实现以下图的基本操作

增加一个新顶点v，InsertVex(G, v)；
删除顶点v及其相关的边，DeleteVex(G, v);
增加一条边<v，w>，InsertArc(G, v, w);
删除一条边<v，w>，DeleteArc(G, v, w)。

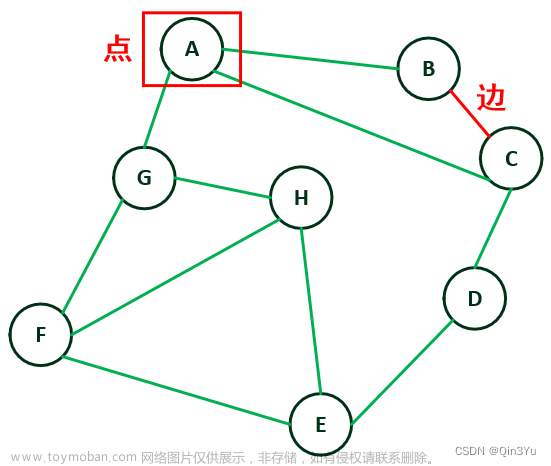
该题所用的图结构

数据结构图增加顶点,算法与数据结构,C/C++,图论,c语言,链表,c++,矩阵

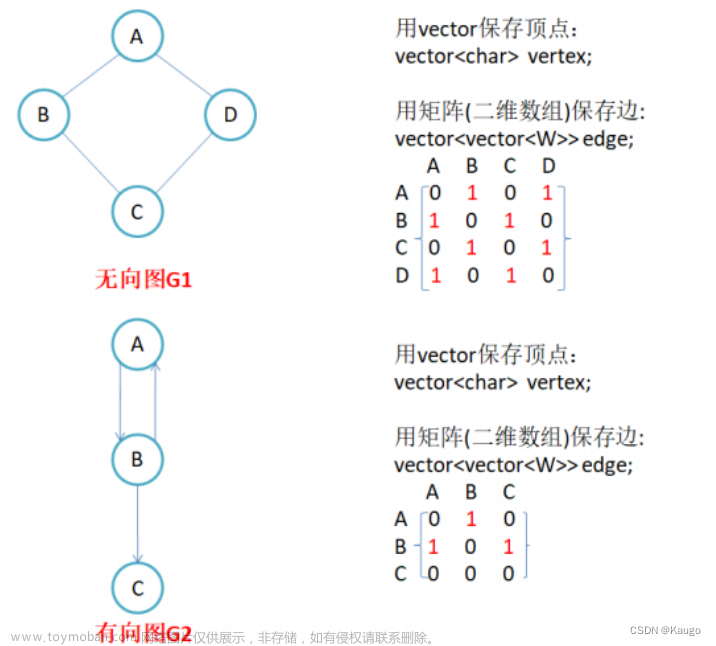
该题所用到的邻接表和邻接矩阵的图形表示

邻接表

数据结构图增加顶点,算法与数据结构,C/C++,图论,c语言,链表,c++,矩阵

邻接矩阵表示

数据结构图增加顶点,算法与数据结构,C/C++,图论,c语言,链表,c++,矩阵

数据结构与定义

因为要分别用邻接表和邻接矩阵来完成上述四个算法，故有两个数据结构的定义

邻接表数据结构定义

#include <stdio.h>
#include <iostream>

using namespace std;

#define MaxSize 20 // 最大顶点的个数
struct Node
{
    int weight;
    int index;
    struct Node *next;
};
struct HNode
{
    char nodeData;
    struct Node *next;
};
struct Graph
{
    int vertexNum;
    int arcNum;
    bool isDireted;
    HNode verList[MaxSize];
};

邻接矩阵数据结构定义

#include <stdio.h>
#include <iostream>

using namespace std;

#define Max 20
// 顶点信息
struct VertexItem
{
    char Vertex; // 顶点信息
    int index;   // 顶点在邻接矩阵中的下标
};
// 图的邻接矩阵存储
struct Graph
{
    int vertexNum;
    int arcNum;
    bool isDireted;
    int Matrix[Max][Max];
    VertexItem vertexList[Max]; // 顶点信息表
};

邻接表

增加一个新顶点v

void InsertVex(Graph &G, char v)
{
    G.verList[G.vertexNum].nodeData = v;
    G.verList[G.vertexNum].next = nullptr;
    G.vertexNum++;
}

删除顶点v及其相关的边

void DeleteVex(Graph &G, char v)
{
    int index = Locate(v, G); // 该顶点的下标
    // 释放与该顶点有关的所有边
    Node *p = G.verList[index].next; // 临时指针p指向该顶点邻接表的第一个结点
    while (p != nullptr)
    {
        if (!G.isDireted) // G为无向图
        {
            Node *q = G.verList[p->index].next; // 临时指针q指向待删除结点所在邻接表中的第一个结点
            while (q->next->index != index)     // 一直找，直到找到q的next结点的index值为删除顶点的index
            {
                q = q->next;
            }
            Node *needDel = q->next; // 创建一个临时指针，指向待删除的结点
            q->next = needDel->next; // 保证邻接表不断
            free(needDel);           // 释放空间
        }
        G.verList[index].next = p->next;
        G.arcNum--;
        free(p);
    }
    // 释放顶点
    G.verList[index].nodeData = NULL;
    G.verList[index].next = nullptr;
    G.vertexNum--;
    return;
}

增加一条边<v，w>

void InsertArc(Graph &G, char tail, char head)
{
    int TailIndex, HeadIndex;
    TailIndex = Locate(tail, G);
    HeadIndex = Locate(head, G);
    if (HeadIndex == -1 || TailIndex == -1) // 输入的弧头或者弧尾不存在
    {
        return;
    }
    // 无论G为有向图还是无向图
    Node *newNode = new Node;
    newNode->next = G.verList[TailIndex].next; // 头插法插入到邻接表中
    newNode->index = HeadIndex;
    G.verList[TailIndex].next = newNode;
    if (!G.isDireted) // G为无向图
    {
        Node *newNode = new Node;
        newNode->next = G.verList[HeadIndex].next; // 头插法插入到邻接表中
        newNode->index = TailIndex;
        G.verList[HeadIndex].next = newNode;
    }
}

删除一条边<v，w>

void DeleteArc(Graph &G, char tail, char head)
{
    int TailIndex = Locate(tail, G);
    int HeadIndex = Locate(head, G);
    Node *p = G.verList[TailIndex].next; // 临时指针p指向弧尾顶点邻接表的第一个结点
    while (p->next->index != HeadIndex)
    {
        p = p->next;
    }
    Node *needDel = p->next;
    p->next = needDel->next;
    free(needDel);
    G.arcNum--;
    if (!G.isDireted) // G为无向图
    {
        Node *q = G.verList[HeadIndex].next;
        while (q->next->index != TailIndex)
        {
            q = q->next;
        }
        needDel = q->next;
        q->next = needDel->next;
        free(needDel);
    }
}

邻接矩阵

增加一个新顶点v

// 添加顶点
void InsertVex(Graph &G, char c)
{
    G.vertexList[G.vertexNum].Vertex = c;          // 顶点信息存入顶点表中
    G.vertexList[G.vertexNum].index = G.vertexNum; // 顶点的在邻接矩阵的索引存入顶点表中                            // 顶点数量加一
    // 对新插入的顶点对应的矩阵初始化
    for (int i = 0; i <= G.vertexNum; i++)
    {
        G.Matrix[G.vertexNum][i] = 0;
        G.Matrix[i][G.vertexNum] = 0;
    }
    G.vertexNum++;
}

删除顶点v及其相关的边

// 删除顶点以及相关的边
void DeletVex(Graph &G, char c)
{
    int vexIndex = Locate(G, c);
    G.vertexNum--;
    for (int i = 0; i < G.vertexNum; i++)
    {
        if (G.Matrix[vexIndex][i] == 1) // 有边
        {
            G.Matrix[vexIndex][i] = 0;
            G.arcNum--;
        }
        if (G.Matrix[i][vexIndex] == 1)
        {
            G.Matrix[i][vexIndex] = 0;
        }
    }
    G.vertexList[vexIndex].index = -1;
}

增加一条边<v，w>

// 添加弧
void InsertArc(Graph &G, char tail, char head)
{
    int tailIndex = Locate(G, tail);
    int headIndex = Locate(G, head);
    if (headIndex == -1 || tailIndex == -1) // 输入的弧头或者弧尾不存在
    {
        return;
    }
    G.Matrix[tailIndex][headIndex] = 1;
    G.arcNum++;
    if (!G.isDireted)
    {
        G.Matrix[headIndex][tailIndex] = 1; // 若不是有向图则再添加一条对称边
    }
}

删除一条边<v，w>

// 删除弧
void DeleteArc(Graph &G, char tail, char head)
{
    int tailIndex = Locate(G, tail);
    int headIndex = Locate(G, head);
    if (headIndex == -1 || tailIndex == -1)
    {
        return;
    }
    G.Matrix[tailIndex][headIndex] = 0;
    G.arcNum--;
    if (!G.isDireted)
    {
        G.Matrix[headIndex][tailIndex] = 0; // 若不是有向图则再删除一条对称边
        G.arcNum--;
    }
}

完整代码

//这个是邻接表的完整代码
#include <stdio.h>
#include <iostream>

using namespace std;

#define MaxSize 20 // 最大顶点的个数
struct Node
{
    int weight;
    int index;
    struct Node *next;
};
struct HNode
{
    char nodeData;
    struct Node *next;
};
struct Graph
{
    int vertexNum;
    int arcNum;
    bool isDireted;
    HNode verList[MaxSize];
};

int Locate(char c, Graph G)
{
    int index = -1;
    for (int i = 0; i < G.vertexNum; i++)
    {
        if (G.verList[i].nodeData == c)
        {
            index = i;
        }
    }
    return index;
}

void InsertVex(Graph &G, char v)
{
    G.verList[G.vertexNum].nodeData = v;
    G.verList[G.vertexNum].next = nullptr;
    G.vertexNum++;
}

void InsertArc(Graph &G, char tail, char head)
{
    int TailIndex, HeadIndex;
    TailIndex = Locate(tail, G);
    HeadIndex = Locate(head, G);
    if (HeadIndex == -1 || TailIndex == -1) // 输入的弧头或者弧尾不存在
    {
        return;
    }
    // 无论G为有向图还是无向图
    Node *newNode = new Node;
    newNode->next = G.verList[TailIndex].next; // 头插法插入到邻接表中
    newNode->index = HeadIndex;
    G.verList[TailIndex].next = newNode;
    if (!G.isDireted) // G为无向图
    {
        Node *newNode = new Node;
        newNode->next = G.verList[HeadIndex].next; // 头插法插入到邻接表中
        newNode->index = TailIndex;
        G.verList[HeadIndex].next = newNode;
    }
}

void DeleteVex(Graph &G, char v)
{
    int index = Locate(v, G); // 该顶点的下标
    // 释放与该顶点有关的所有边
    Node *p = G.verList[index].next; // 临时指针p指向该顶点邻接表的第一个结点
    while (p != nullptr)
    {
        if (!G.isDireted) // G为无向图
        {
            Node *q = G.verList[p->index].next; // 临时指针q指向待删除结点所在邻接表中的第一个结点
            while (q->next->index != index)     // 一直找，直到找到q的next结点的index值为删除顶点的index
            {
                q = q->next;
            }
            Node *needDel = q->next; // 创建一个临时指针，指向待删除的结点
            q->next = needDel->next; // 保证邻接表不断
            free(needDel);           // 释放空间
        }
        G.verList[index].next = p->next;
        G.arcNum--;
        free(p);
    }
    // 释放顶点
    G.verList[index].nodeData = NULL;
    G.verList[index].next = nullptr;
    G.vertexNum--;
    return;
}

void DeleteArc(Graph &G, char tail, char head)
{
    int TailIndex = Locate(tail, G);
    int HeadIndex = Locate(head, G);
    Node *p = G.verList[TailIndex].next; // 临时指针p指向弧尾顶点邻接表的第一个结点
    while (p->next->index != HeadIndex)
    {
        p = p->next;
    }
    Node *needDel = p->next;
    p->next = needDel->next;
    free(needDel);
    G.arcNum--;
    if (!G.isDireted) // G为无向图
    {
        Node *q = G.verList[HeadIndex].next;
        while (q->next->index != TailIndex)
        {
            q = q->next;
        }
        needDel = q->next;
        q->next = needDel->next;
        free(needDel);
    }
}
void CreateGraph(Graph &G)
{
    cin >> G.vertexNum >> G.arcNum; // 输入顶点数和边数
    cin >> G.isDireted;             // 输入是否为有向图
    if (G.vertexNum > MaxSize)
    {
        return;
    }
    // 初始化顶点列表
    for (int i = 0; i < G.vertexNum; i++)
    {
        cin >> G.verList[i].nodeData;
        G.verList[i].next = nullptr;
    }
    // 依次输入各边的信息
    for (int j = 0; j < G.arcNum; j++)
    {
        char ArcHead, ArcTail;
        cin >> ArcTail >> ArcHead;
        InsertArc(G, ArcTail, ArcHead);
    }
}

void HNodeIndegree(Graph G)
{
    int IndegreeCnt[G.vertexNum] = {0};
    for (int i = 0; i < G.vertexNum; i++)
    {
        Node *tmp = G.verList[i].next;
        while (tmp != nullptr)
        {
            IndegreeCnt[tmp->index]++;
            tmp = tmp->next;
        }
    }
    cout << "all node's indegree" << endl;
    for (int j = 0; j < G.vertexNum; j++)
    {
        cout << G.verList[j].nodeData << ':' << IndegreeCnt[j] << endl;
    }
}

void HNodeOutdegree(Graph G)
{
    int OutdegreeCnt[G.vertexNum] = {0};
    for (int i = 0; i < G.vertexNum; i++)
    {
        Node *tmp = G.verList[i].next;
        while (tmp != nullptr)
        {
            OutdegreeCnt[i]++;
            tmp = tmp->next;
        }
    }
    cout << "all node's outdegree" << endl;
    for (int j = 0; j < G.vertexNum; j++)
    {
        cout << G.verList[j].nodeData << ':' << OutdegreeCnt[j] << endl;
    }
}

void MaxOutDegreeNode(Graph G)
{
    int index = -1; // 出度最大的数组下标
    int res = 0;    // 出度
    // 与HNodeOutdegree同
    // same code
    int OutdegreeCnt[G.vertexNum] = {0};
    for (int i = 0; i < G.vertexNum; i++)
    {
        Node *tmp = G.verList[i].next;
        while (tmp != nullptr)
        {
            OutdegreeCnt[i]++;
            tmp = tmp->next;
        }
    }
    // same code

    for (int j = 0; j < G.vertexNum; j++)
    {
        if (OutdegreeCnt[j] > res)
        {
            res = OutdegreeCnt[j];
            index = j;
        }
    }
    cout << "the max out degree is" << ':' << G.verList[index].nodeData << endl;
}

void ZeroOutdegree(Graph G)
{
    int cnt = 0;
    // same code
    int OutdegreeCnt[G.vertexNum] = {0};
    for (int i = 0; i < G.vertexNum; i++)
    {
        Node *tmp = G.verList[i].next;
        while (tmp != nullptr)
        {
            OutdegreeCnt[i]++;
            tmp = tmp->next;
        }
    }
    // same code
    for (int j = 0; j < G.vertexNum; j++)
    {
        if (OutdegreeCnt[j] == 0)
        {
            cnt++;
        }
    }
    cout << "the number of zero outdegree is" << ' ' << cnt;
}

bool IsArcExist(char a, char b, Graph G)
{
    int AIndex, BIndex; // 找到弧头和弧尾的数组下标
    for (int i = 0; i < G.vertexNum; i++)
    {
        if (G.verList[i].nodeData == a)
        {
            AIndex = i;
            continue;
        }
        if (G.verList[i].nodeData == b)
        {
            BIndex = i;
            continue;
        }
    }
    Node *tmp = G.verList[AIndex].next;
    while (tmp != nullptr)
    {
        if (tmp->index == BIndex)
        {
            return true;
        }
        tmp = tmp->next;
    }
    return false;
}

int main()
{
    Graph G;
    CreateGraph(G);
    // HNodeIndegree(G);
    // HNodeOutdegree(G);
    // MaxOutDegreeNode(G);
    // ZeroOutdegree(G);
    // char head, tail;
    // cin >> head >> tail;
    // bool isit = IsArcExist(head, tail, G);
    // cout << isit << endl;
    return 0;
}

//这个是邻接矩阵的完整代码
#include <stdio.h>
#include <iostream>

using namespace std;

#define Max 20
// 顶点信息
struct VertexItem
{
    char Vertex; // 顶点信息
    int index;   // 顶点在邻接矩阵中的下标
};
// 图的邻接矩阵存储
struct Graph
{
    int vertexNum;
    int arcNum;
    bool isDireted;
    int Matrix[Max][Max];
    VertexItem vertexList[Max]; // 顶点信息表
};
// 初始化图
void InitGraph(Graph &G)
{
    G.arcNum = 0;
    G.vertexNum = 0;
    for (int i = 0; i < Max; i++)
    {
        for (int j = 0; j < Max; j++)
        {
            G.Matrix[i][j] = -1;
        }
    }
}
// 获取顶点下标
int Locate(Graph G, char c)
{
    int res = -1;
    for (int i = 0; i < G.vertexNum; i++)
    {
        if (G.vertexList[i].Vertex == c)
        {
            res = G.vertexList[i].index;
        }
    }
    return res;
}
// 创造图
void CreateGraph(Graph &G)
{
    if (G.vertexNum > Max) // 输入的顶点数量超过最大值
    {
        return;
    }
    //
    for (int i = 0; i < G.vertexNum; i++)
    {
        for (int j = 0; j < G.vertexNum; j++)
        {
            G.Matrix[i][j] = 0;
        }
    }
    for (int i = 0; i < G.vertexNum; i++)
    {
        char vertex;
        cin >> vertex;
        G.vertexList[i].Vertex = vertex;
        G.vertexList[i].index = i;
    }
    char tail, head; // 弧尾和弧头
    for (int i = 0; i < G.arcNum; i++)
    {
        cin >> tail >> head;
        int tailIndex, headIndex;
        tailIndex = Locate(G, tail);
        headIndex = Locate(G, head);
        // G为有向图
        if (G.isDireted)
        {
            G.Matrix[tailIndex][headIndex] = 1;
        }
        // G为无向图
        else
        {
            G.Matrix[tailIndex][headIndex] = 1;
            G.Matrix[headIndex][tailIndex] = 1;
        }
    }
}
// 添加顶点
void InsertVex(Graph &G, char c)
{
    G.vertexList[G.vertexNum].Vertex = c;          // 顶点信息存入顶点表中
    G.vertexList[G.vertexNum].index = G.vertexNum; // 顶点的在邻接矩阵的索引存入顶点表中                            // 顶点数量加一
    // 对新插入的顶点对应的矩阵初始化
    for (int i = 0; i <= G.vertexNum; i++)
    {
        G.Matrix[G.vertexNum][i] = 0;
        G.Matrix[i][G.vertexNum] = 0;
    }
    G.vertexNum++;
}
// 删除顶点以及相关的边
void DeletVex(Graph &G, char c)
{
    int vexIndex = Locate(G, c);
    G.vertexNum--;
    for (int i = 0; i < G.vertexNum; i++)
    {
        if (G.Matrix[vexIndex][i] == 1) // 有边
        {
            G.Matrix[vexIndex][i] = 0;
            G.arcNum--;
        }
        if (G.Matrix[i][vexIndex] == 1)
        {
            G.Matrix[i][vexIndex] = 0;
        }
    }
    G.vertexList[vexIndex].index = -1;
}
// 添加弧
void InsertArc(Graph &G, char tail, char head)
{
    int tailIndex = Locate(G, tail);
    int headIndex = Locate(G, head);
    if (headIndex == -1 || tailIndex == -1) // 输入的弧头或者弧尾不存在
    {
        return;
    }
    G.Matrix[tailIndex][headIndex] = 1;
    G.arcNum++;
    if (!G.isDireted)
    {
        G.Matrix[headIndex][tailIndex] = 1; // 若不是有向图则再添加一条对称边
    }
}
// 删除弧
void DeleteArc(Graph &G, char tail, char head)
{
    int tailIndex = Locate(G, tail);
    int headIndex = Locate(G, head);
    if (headIndex == -1 || tailIndex == -1)
    {
        return;
    }
    G.Matrix[tailIndex][headIndex] = 0;
    G.arcNum--;
    if (!G.isDireted)
    {
        G.Matrix[headIndex][tailIndex] = 0; // 若不是有向图则再删除一条对称边
        G.arcNum--;
    }
}

int main()
{
    Graph G;
    InitGraph(G);
    cin >> G.vertexNum >> G.arcNum;
    cin >> G.isDireted;
    CreateGraph(G);
    InsertVex(G, '6');      // 插入新顶点6
    InsertVex(G, '7');      // 插入新顶点7
    InsertArc(G, '1', '6'); // 添加一条边，从1 -> 6
    InsertArc(G, '3', '6'); // 添加一条边，从3 -> 6
    InsertArc(G, '1', '7'); // 添加一条边，从1 -> 7
    InsertArc(G, '3', '7'); // 添加一条边，从3 -> 7
    DeletVex(G, '6');       // 删除顶点6以及其关联的所有边
    DeleteArc(G, '1', '6'); // 删除1->6的边
    return 0;
}

结束语

因为是算法小菜，所以提供的方法和思路可能不是很好，请多多包涵~如果有疑问欢迎大家留言讨论，你如果觉得这篇文章对你有帮助可以给我一个免费的赞吗？我们之间的交流是我最大的动力！文章来源地址https://www.toymoban.com/news/detail-753765.html

到了这里，关于【数据结构与算法】分别以邻接矩阵和邻接表作为存储结构实现以下操作：1.增加一个新顶点v、2.删除顶点v及其相关的边、3.增加一条边＜v，w＞、4.删除一条边＜v，w＞的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！