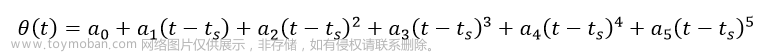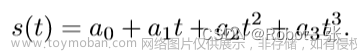学习目的:
理解轨迹规划原理;学会用轨迹规划处理实际问题。
学习内容:
轨迹规划原理;关节空间的轨迹规划;直角坐标空间的轨迹规划;连续轨迹记录。
1.引言
根据前几章可知,只要知道机器人的关节变量就能确定机器人的位置,或者已知机器人的位置就能确定相应的关节变量以及速度。但是机器人位置变换的过程怎样以及如何让一个机器人的末端执行器按照我们规划的路径从一个位置移动到另一个位置,这是本章要研究的内容。
2.路径与轨迹
路径:如果规定一个机器人从A点经过B点运动到C点而不强调时间的概念,那么这一过程中的位型序列就构成了一条路径。
轨迹:如果我们强调到达其中任意一点的时间,那么这就是一条轨迹。
我们可以看出轨迹和路径的区别就在于轨迹依赖速度和加速度。

因为机器人工作的过程中,不仅要关注路径,同样要关注轨迹,比如焊接机器人,因此,本章主要研究机器人的轨迹。
3.关节空间描述与直角空间描述
关节空间描述:如果给定机器人运动的起点和终点,就可以利用逆运动学方程计算出每个关节的矢量角度值;然后机器人控制器驱动关节电机运动使机器人到达相应的位置。这种以关节角度的函数来描述机器人轨迹的方法称为关节空间法。
特点:在机器人运动的过程中,中间状态是不可知的;但是计算量较小,不会出现奇异点。
直角坐标空间描述:
将轨迹分为若干段,使机器人的运动经过这些中间点,在每一点都求解机器人的关节变量,直到到达终点,如下图所示:

这里机器人在所有时刻的运动都是已知的。机器人所产生的运动序列首先在直角坐标系中进行描述,然后转化为关节空间描述。
特点:路径可控可预知,直观容易看到机器人末端轨迹;但计算量大,容易出现奇异点,如下图所示:

其原因使具体运动之前无法得知其位姿。
4.轨迹规划的基本原理
关节空间的轨迹规划
例子:以简单的2自由度机器人为例,介绍在关节空间和直角坐标空间进行轨迹规划的基本原理。如下图所示:
已知两个关节运动的最大速率为10度/s
不同运动方式的轨迹展示:
各关节都以最大角速度运动:
特点:轨迹不规则,末端走过距离不均匀,且各关节不是同时到达。

在以上基础上对关节速率做归一化处理 ,使各关节同时到达终点。
特点:各关节同时到达终点,轨迹各部分比较均衡,但所的路径仍然是不规则的。

这两种方案都是在关节空间中进行规划的,所需的计算仅是运动终点的关节量,第二种方案还进行了关节速度的归一化处理。根据结果可以看到,关节空间的这两种规划方案运动轨迹都是不规则的,是运动结果的呈现,而不是提前规划好的。而这在有些机器人的运动控制中是不允许的。
直角坐标空间轨迹规划
首先画出路径,接着将路径n等分,分别计算到达各点所需要的关节变量。
特点:关节角非均匀变化,末端沿已知路径行走。但在点与点之间不能保证严格按照直线运动。

问题: 这里假设了机器人的驱动装置能偶提供足够大的功率来妈祖关节所需的加速和减速,但如果在第一段运动不能立刻加速到所需要的速度,机器人所沿循的轨迹将稍稍落后于设想的轨迹。

需要注意,两个连续的关节量之间的差值大于预定的最大关节速度10度/s。

第一个关节向上移动前,先向下移动。

在以上基础上,考虑各关节的加速减速时间。即:开始时路径分段较小,随后以恒定速度运动,接近B点时再在较小的分段上减速。这里开始时基于方程x=1/2a进行划分,知道达到需要的运动速度为止,末端以减速过程类似规划。

这里讨论了直线轨迹规划,实际上,机器人应用中,很多情况时曲线路径(比如二次曲线),这时也必须基于期望的路径计算每一段的坐标,进而计算关节量,才能规划出机器人沿期望的路径运动轨迹。
除了两点之间的运动,多数情况下还会要求机器人顺序经过许多点,包括中间点或过渡点。下面讨论多点间的运动轨迹。
多点的情况:假设机器人要从A经过B到达C,可以有几种运动方案:
从A到B先加速,再匀速,接近B时再减速,从B到C再重复。为避免B点停顿,可以将B点两边的动作平滑过渡。

考虑到由于采用了平滑过渡曲线,机器人经过的可能不是原来的B点,可事先设定一个不同的点,使曲线正好经过B点。

在B点前后加过渡点D E,使B落在D E上。

轨迹规划的分类
PTP(点到点运动):对于点位作业机器人(比如装配机器人),需要描述它的起始状态和目标状态,如果用T0表示工具坐标系的起始值,Tf表示目标值,就是表示这两个值的相对关系。
CP(连续路径运动或轮廓运动):不仅要规定起始点和终止点,还要规定中间整个运动过程,对于一段连续运动过程,理论上无法精确实现,实际上是选取一定数量的点作为中间点,从而近似实现沿给定的路径运动。
障碍约束轨迹规划
下面将用多项式来表示两个路段之间,每个点的位置,速度和加速度。当规划路径之后,通过路径信息求解逆运动学方程得到关节变量,并操纵机器人做相应运动。
如果机器人的路径非常复杂,无法用一个方程表示,可以用手移动机器人,并记录下每个关节的运动状态,根据这些关节值,驱动机器人运动,再现机器人的动作,比如汽车喷漆,复杂焊缝得得焊接等,这就是示教机器人。
5.关节空间的轨迹规划
一些前提:假设机器人的初始位姿是已知的,通过求解逆运动学方程可以求得机器人期望末端位姿对应的关节角;机器人的每个关节的运动必须单独规划;若考虑某个关节再运动开始时刻ti的角度为,希望该关节在时刻tf运动到新的角度;轨迹规划的一种方法是使用多项式函数,以使初始和末端的边界条件与已知条件相匹配。这些已知条件为和及机器人开始运动和结束运动时的速度。
三次多项式的轨迹规划:
我们假设四个已知条件的机器人某一关节的运动方程可以用一三次多项式表示:


如果要求机器人末端一次通过两个以上的点,则每一段求解出的边界速度和位置均可作为下一段的初始条件,其余相同。
五次多项式轨迹规划:
前面的三次多项式轨迹规划,加速度无法在实际过程中实现,因此,除了制定运动段的起点终点以及起点终点的速度以外,还应指定起点和终点的加速度。这样,边界条件增加到了6个,应该采用五次多项式描述:

同样,可以根据位置,速度,加速度边界条件计算出五次多项式的系数。
抛物线过渡的线性运动轨迹:
在机器人关节以恒定速度运动时,起点和终点处需要用抛物线过渡。如图所示
抛物线段的方程:

将边界条件代入抛物线方程,得到:

从而给出抛物线段的方程为:

A,B点以及终点的关节位置和速度如下:

由上式可以求解过渡时间:

以上讨论是在运动段的初始时间为0的前提下,但如果初始时间为t,可以通过平移坐标轴的方法使初始时间为0,如下:

高次多项式运动轨迹:略
6.直角坐标空间的轨迹规划
所有用于关节空间轨迹规划的方法都可用于直角坐标空间的轨迹规划。最根本的差别在于,直角坐标空间轨迹规划必须反复求解逆运动学方程来计算关节角。
下面是直角坐标空间轨迹规划的计算循环:

为实现一条直线轨迹,必须计算起点和终点位姿之间的变换,并将给变换划分为许多小段。下面是起点构型和终点构型之间的总变换R:

至少有以下三种不同的方法可用来将该总变换化为许多的小段变换。
(1)希望在起点和终点之间有平滑的线性变换,因此需要大量很小的分段,从而产生了大量的微分运动。利用上一章导出的微分运动方程,可将末端手坐标系在每个新段的位姿与微分运动,雅克比矩阵及关节速度通过下列方程联系到一起。

这一方法需要进行大量的计算,并且仅当雅可比矩阵逆存在时才有效。
(2)在起点和终点之间的变换分解为一个平移和两个旋转。平移是将坐标原点从起点移动到终点,第一个旋转是将末端手坐标系与期望姿态对准,而第二个旋转是手坐标系绕其自身周转到最终的姿态。所有者三个变换同时进行。
(3)在起点和终点的变换R分解为一个平移和一个K轴的旋转。平移仍是将坐标原点从起点移动到终点,而旋转则是将手臂坐标系与最终的期望姿态对准。连个变换同时进行。

7.连续轨迹记录
示教回放机器人:有时任务太复杂或轨迹难以表示,可以首先示教机器人如何运动,同时记录这些运动数据,然后回放所记录的运动并执行该运动。在整个运动过程中都必须不断地采样并记录关节量,此后通过回放采样数据并驱动机器人的关节来驱动是机器人跟踪做记录的轨迹,从而完成所规划的任务。
特点:所需的编程和计算量较少,但需要精确执行,采样和记录所有的运动,每当部分运动需要改变时就必须重新示教编程。
8.本章总结
轨迹规划即可在关节空间进行也可在直角坐标进行,在两种空间的许多方法可以通用。
直角坐标空间的轨迹规划比较直观,但较难计算和规划,对于已经指定的路径必须在执教空间进行规划才能实现。文章来源:https://www.toymoban.com/news/detail-754272.html
如果没有指定机器人的路径,则关节空间的轨迹规划更容易计算。文章来源地址https://www.toymoban.com/news/detail-754272.html
到了这里,关于机器人期末复习 第五章 轨迹规划的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!