个人主页:仍有未知等待探索_C语言疑难,数据结构,小项目-CSDN博客
专题分栏:数据结构_仍有未知等待探索的博客-CSDN博客
一、前言
树形结构是一类非常重要的非线性结构。树形结构是节点之间有分支,并且具有层次关系的结构,它类似于自然界中的树。
就比如说:电脑中磁盘中的文件储存方式就类似于一颗树。
二、树的定义和基本的术语
在讲二叉树之前,我们要先讲树的定义和树的一些术语。
1、树的定义
树是n(n>=0)个结点的有限集,T为空时称为空树。
非空树的特点:
- T中有且仅有一个结点K,没有前驱,称K为树的根结点。
- 除了根结点以外,其余节点有且仅有一个直接前驱。
- T中各结点可以有0个或者多个后继。
- 除了根节点以外,其余结点可以分为m个互不相干的有限集合。
2、树的基本术语
- 一个节点拥有的子树个数称为结点的度。
- 度为零的结点称为叶子节点。
- 树的度是树中所有结点的度的最大值。
- 结点子树的根称为孩子结点,该结点称为其双亲结点。
- 结点的祖先是从跟到该结点所经分支上的所有结点。
- 某一结点的子孙是以该结点为根的子树上的任一结点。
- 结点的层次:根为第一层,以此类推。
- 树中最大的层次叫做树的深度(高度)。
- 树中结点的个子树可以看作是从左到右有次序的,称为有序树,反之无序树。
- 森林是m(m>=0)棵互不相交的树的集合。
三、二叉树
1、二叉树的5种基本形态

2、二叉树的两种特殊形态
(1)满二叉树
每层结点都是满的,即满二叉树的每层上的结点数都是最大结点数。
一共有2^n-1个结点(n为树的高度)
下图是高度为4的满二叉树
(2)完全二叉树
最多只有一个度为1的结点。
序号和满二叉树的一样。
3、二叉树的性质
- 在二叉树的第i层上至多有 2^i - 1 个结点( i >= 1 )。
- 深度为k的二叉树至多有 2^k - 1 个结点( k >= 1 )。
- 设n0、n1、n2分别为度为0,1,2的结点,则 n0=n2+1 。
- 具有n个结点的完全二叉树的深度 [log2n]+1 。
- n个完全二叉树,按照层序编号,i=1,其结点为根节点。若 i > 1,i/2 为其结点的双亲结点,2*i 为其左孩子的编号(2*i > n 无左孩子), 2*i+1为其右孩子的编号 (2*i +1 > n 无右孩子)。
4、二叉树的存储结构
(1)顺序存储结构
#define MAX 100
typedef int BT;
struct BiTree
{
BT tree[MAX];
int n;
};
(2)链式存储结构
// 二叉链树
typedef int TreeNodeType;
struct Bitree
{
TreeNodeType data;
struct Bitree* left, *right;
};// 三叉链树
typedef int TreeNodeType;
struct Bitree
{
TreeNodeType data;
struct Bitree* left, * right;
struct Bitree* parent;
};5、二叉树的遍历

(1)先序遍历
遍历的顺序是:根结点、左结点、右结点。
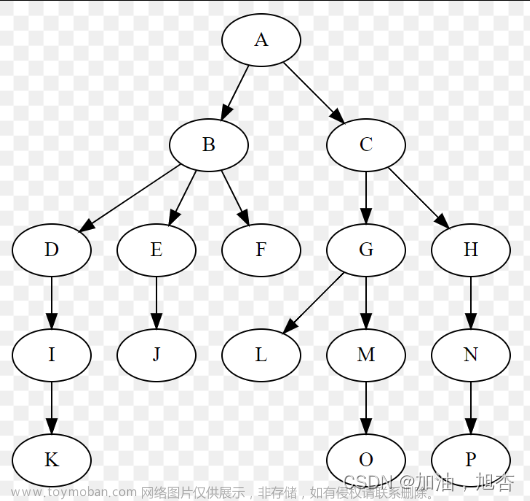
就比如上图的先序遍历是:A B D E C F
void PreOrder(BiTree bt) { //如果bt为空的话,就退出。 if (bt == NULL) return; visit();//访问根节点 PreOrder(bt->left);//先序遍历左子树,递归调用 PreOrder(bt->right);//先序遍历右子树,递归调用 }
(2)中序遍历
遍历的顺序是:左结点、根节点、右结点。
上图的中序遍历是:D B E A F C
void InOrder(BiTree bt) { //如果bt为空的话,就退出。 if (bt == NULL) return; InOrder(bt->left);//中序遍历左子树,递归调用 visit();//访问根节点 InOrder(bt->right);//中序遍历右子树,递归调用 }
(3)后序遍历
遍历的顺序是:左结点、右结点、根节点。
上图的后序遍历是:D E B F C A
void PostOrder(BiTree bt) { //如果bt为空的话,就退出。 if (bt == NULL) return; PostOrder(bt->left);//中序遍历左子树,递归调用 PostOrder(bt->right);//中序遍历右子树,递归调用 visit();//访问根节点 }
(4)层序遍历
层序遍历的顺序:按二叉树从上到下,从左到右依次访问每个节点中存储的数据。
上图的层序遍历是:A B C D E F
#define MAX 100 void LevelOrder(BiTree bt) { if (bt == NULL) return; //队列 BiTree Queue[MAX] = { 0 }; int front = 0, rear = 0; //根节点入队 Queue[rear] = bt; rear = (rear + 1) % MAX; while (rear != front) { //访问队内第一个元素 visit(Queue[front]); //如果队内第一个元素的左孩子不为空的话,入队 if (Queue[front]->left != NULL) { Queue[rear] = Queue[front]->left; rear = (rear + 1) % MAX; } //如果队内第一个元素的右孩子不为空的话,入队 if (Queue[front]->right != NULL) { Queue[rear] = Queue[front]->right; rear = (rear + 1) % MAX; } //队内第一个元素出队 front = (front + 1) % MAX; } }
6、求二叉树的高度(深度)
用递归的思想:将一个大问题转化为具有相同性质的小问题。
二叉树的高度=max(左子树的高度,右子树的高度)
int BiTreeDepth(BiTree bt) { if (bt == NULL) { return 0; } int dl = 0, dr = 0, d = 0; dl = BiTreeDepth(bt->left);//求左子树的高度 dr = BiTreeDepth(bt->right);//求右子树的高度 d = dl > dr ? dl : dr;//求树的高度 return d + 1; }
7、求叶子结点的个数
叶子节点的个数=左子树的叶子节点的个数+右子树的叶子节点的个数
int BiTreeLeaf(BiTree bt) { //如果为空树,叶子结点为0 if (bt == NULL) return 0; //判断是否是叶子结点 if (bt->left == NULL && bt->right == NULL) return 1; //返回总数 return (BiTreeLeaf(bt->left) + BiTreeLeaf(bt->right)); }
8、根据先序序列和中序序列创建二叉树
也可以根据后序序列和中序序列来进行创建二叉树
//根结点
BiTree bt = NULL;
BiTree PreInBiTreeCreate(int Pre[], int In[], int i, int j, int k, int h)
{
//开辟空间
bt = (BiTree)malloc(sizeof(struct BiTree));
assert(bt);
//将根结点的数据放入结构体中
bt->data = Pre[i];
bt->left = NULL;
bt->right = NULL;
int m = k;
//找根结点的位置
while (Pre[i] != In[m])
m++;
//如果m==k,bt没有左孩子
if (m == k)
bt->left = NULL;
else
bt->left = PreInBiTreeCreate(Pre, In, i + 1, i + m - k, k, m - 1);
//如果m==h,bt没有右孩子
if (m == h)
bt->right = NULL;
else
bt->right = PreInBiTreeCreate(Pre, In, i + m - k + 1, j, m + 1, h);
}文章来源:https://www.toymoban.com/news/detail-754284.html
谢谢大家的支持! 文章来源地址https://www.toymoban.com/news/detail-754284.html
到了这里,关于C/C++【数据结构】一文秒懂二叉树的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!