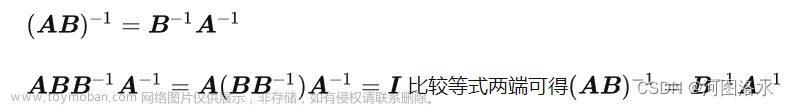5.4 满秩分解-Toy模板网

这篇具有很好参考价值的文章主要介绍了5.4 满秩分解。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

原理

任意矩阵都有满秩分解Full rank factorization。也就是说不限于方阵，更不限于满秩矩阵。满秩分解用途很广，尤其是后期的对于广义逆的学习来说非常重要。
首先要搞清楚什么是满秩分解full rank factorization，假设矩阵为 $A$ ,它的秩为 $r$ ，满秩分解就是分解为如下两个矩阵相乘：
$A^{m \times n}=B^{m \times r}C^{r \times n}$
要求就是B和C的秩都是 $r$ ，也就是说 $B$ 是列满秩， $C$ 是行满秩。
那么怎么进行满秩分解呢？只需要用到初等含变换就行了。将矩阵通过初等行变换变成拟Hermite标准型H。那么问题来了，什么是拟Hermite标准型ansi Hermite canonical form？拟埃尔米特标准型的意思是第r行以下全是0，并且存在r列，这r列是单位矩阵的列。如果这r列的组成单位矩阵是顺序的，那么就是埃尔米特标准型。
得到了拟埃尔米特标准型H之后，H的前r行就是C矩阵，原矩阵组成单位矩阵的列，按单位顺序排好就是B矩阵。满秩分解就完成了，所以也挺简单的。

举例

我们以一个 $\times 5$ 矩阵开始：
$\begin{pmatrix}3 & 1 & 0 & -1 & 1\\ 0 & 1 & 1 & 0 & 2\\ 1 & -1 & -1 & 2 & -1\\ 7 & 2 & 0 & 0 & 3\\ \end{pmatrix}\\ \sim \begin{pmatrix}1 & \frac13 & 0 & -\frac13 & \frac13\\ 0 & 1 & 1 & 0 & 2\\ 0 & -\frac43 & -1 & \frac73 & -\frac43\\ 0 & -\frac13 & 0 & \frac73 & \frac23\\ \end{pmatrix}\\ \sim \begin{pmatrix}1 & 0 & -\frac13 & -\frac13 & -\frac13\\ 0 & 1 & 1 & 0 & 2\\ 0 & 0 & \frac13 & \frac73 & \frac43\\ 0 & 0 & \frac13 & \frac73 & \frac43\\ \end{pmatrix}\\ \sim \begin{pmatrix}1 & 0 & 0 & 2 & 1\\ 0 & 1 & 0 & -7 & -2\\ 0 & 0 & 1 & 7 & 4\\ 0 & 0 & 0 & 0 & 0\\ \end{pmatrix}\\ B= \begin{pmatrix}3 & 1 & 0\\ 0 & 1 & 1\\ 1 & -1 & -1\\ 7 & 2 & 0\\ \end{pmatrix}\\ C=\begin{pmatrix}1 & 0 & 0 & 2 & 1\\ 0 & 1 & 0 & -7 & -2\\ 0 & 0 & 1 & 7 & 4\\ \end{pmatrix}\\$

Python代码

我是用直接把前r列化成单位矩阵的方法得到埃尔米特标准型，这样计算比较机械，也容易实现，代码如下：文章来源地址https://www.toymoban.com/news/detail-754301.html

    # 矩阵的满秩分解
    def full_rank_factorization(self):
        # 对第i列，第i行变1，其余行变0
        array = copy.deepcopy(self.__vectors)
        m = len(self.__vectors[0])
        n = len(self.__vectors)
        r = min(m, n)
        # i 是列
        for i in range(r):
            # 先处理对角线元素
            # 近似为0
            if abs(array[i][i]) < MAX_ERROR:
                break
            row_times(array, i, 1 / array[i][i])

            # 是行
            vector = array[i]
            for j in range(m):

                if i == j:
                    continue
                # 处理非对角线元素，就变成0吧
                row_times_add(array, i, -vector[j], j)
            print("~",Matrix(array).to_latex())
        rank = 0
        # 检查每一行是否全为0
        for i in range(m):
            if all_zero_row(array, i):
                continue
            rank += 1
        print(Matrix(array).to_latex())
        b = Matrix(self.__vectors[0:rank])
        c = Matrix(first_rows(array, rank))
        return b, c