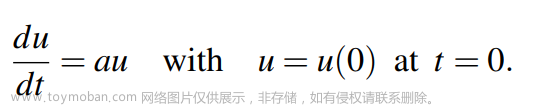这篇具有很好参考价值的文章主要介绍了【问题证明】矩阵方程化为特征值方程求得的特征值为什么是全部特征值？不会丢解吗？。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。
这个问题困扰了我好久，一直感觉如果有其他的特征值没法证伪，不过一直存在思想的层面，没有实际解决，今天突然想到动笔来解决，遂得解，证明如下。
文章来源：https://www.toymoban.com/news/detail-754354.html
这个证明看似证明过后很直观，但实际上思维走向了牛角尖的时候光靠思考是无法得出令人信服的结论的，唯有实际动笔之后可能才会得出真实有用的结论。不知道是不是我是唯一一个对这个事情感觉到很困惑的哈哈哈，，，网上真的是没有看到和我有同样困惑丢没丢解的人，如果有同样困惑的小伙伴欢迎留言hhh，真的烦了我好久。。。文章来源地址https://www.toymoban.com/news/detail-754354.html
到了这里，关于【问题证明】矩阵方程化为特征值方程求得的特征值为什么是全部特征值？不会丢解吗？的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处： 如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！
设n阶矩阵 A A A 的特征值为 λ 1 , λ 2 , . . , λ n lambda_1, lambda_2,..,lambda_n λ 1 , λ 2 , .. , λ n ，则 λ 1 λ 2 ⋯ λ n = ∣ A ∣ 。 lambda_1lambda_2cdotslambda_n = |A|。 λ 1 λ 2 ⋯ λ n = ∣ A ∣ 。 证明： 矩阵 A A A 的特征多项式为： f ( λ ) = ∣ λ E − A ∣ = ∣ λ − a 11 −
目录 一. 特征值介绍 二. 单变量常微分方程 三. 利用矩阵解决微分方程问题 四. 小结 4.1 矩阵论 4.2 特征值与特征向量内涵 4.3 应用 线性代数有两大基础问题： 如果A为对角阵的话，那么问题就很好解决。需要注意的是，矩阵的基础行变换会改变特征值的大小。 在已知解的情况
性质 1 设 n n n 阶矩阵 A = ( a i j ) boldsymbol{A} = (a_{ij}) A = ( a ij ) 的特征值为 λ 1 , λ 2 , ⋯ , λ n lambda_1,lambda_2,cdots,lambda_n λ 1 , λ 2 , ⋯ , λ n ，则 λ 1 + λ 2 + ⋯ + λ n = a 11 + a 22 + ⋯ + a n n lambda_1 + lambda_2 + cdots + lambda_n = a_{11} + a_{22} + cdots + a_{nn} λ 1 + λ 2
性质 1 设 n n n 阶矩阵 A = ( a i j ) boldsymbol{A} = (a_{ij}) A = ( a ij ) 的特征值为 λ 1 , λ 2 , ⋯ , λ n lambda_1,lambda_2,cdots,lambda_n λ 1 , λ 2 , ⋯ , λ n ，则 λ 1 λ 2 ⋯ λ n = ∣ A ∣ lambda_1 lambda_2 cdots lambda_n = |boldsymbol{A}| λ 1 λ 2 ⋯ λ n = ∣ A ∣ 。 证明 不妨设
性质 1 设 n n n 阶矩阵 A = ( a i j ) boldsymbol{A} = (a_{ij}) A = ( a ij ) 的特征值为 λ 1 , λ 2 , ⋯ , λ n lambda_1,lambda_2,cdots,lambda_n λ 1 , λ 2 , ⋯ , λ n ，则 λ 1 + λ 2 + ⋯ + λ n = a 11 + a 22 + ⋯ + a n n lambda_1 + lambda_2 + cdots + lambda_n = a_{11} + a_{22} + cdots + a_{nn} λ 1 + λ 2
谱图使用标准化拉普拉斯矩阵 L n o r m L^{norm} L n or m 的一个重要原因就是， L n o r m L^{norm} L n or m 比拉普拉斯矩阵 L L L 稳定。很多资料只是简单地介绍了 L n o r m L^{norm} L n or m ，在kipfGCN中也只是简单地提到 L n o r m L^{norm} L n or m 的特征值不大于2。本文搜集了相关lecture，并推导
参考视频：https://www.bilibili.com/video/BV1Vg41197ew/?vd_source=7a1a0bc74158c6993c7355c5490fc600 参考资料(半正定矩阵的定义)：https://baike.baidu.com/item/%E5%8D%8A%E6%AD%A3%E5%AE%9A%E7%9F%A9%E9%98%B5/2152711?fr=ge_ala 看看半正定矩阵的定义： 正定矩阵是 0，半正定矩阵是 = 0 根据定义来看，半正定矩阵也有 “实
前置定理 1 任给二次型 f = ∑ i , j = 1 n a i j x i x j ( a i j = a j i ) f = sum_{i,j=1}^n a_{ij} x_i x_j (a_{ij} = a_{ji}) f = ∑ i , j = 1 n a ij x i x j ( a ij = a ji ) ，总有正交变换 x = P y boldsymbol{x} = boldsymbol{P} boldsymbol{y} x = P y ，使 f f f 化为标准形 f = λ 1 y 1 2 + λ 2 y 2 2 + ⋯
当一个矩阵具有重复的特征值时，意味着存在多个线性无关的特征向量对应于相同的特征值。这种情况下，我们称矩阵具有重复特征值。 考虑一个n×n的矩阵A，假设它有一个重复的特征值λ，即λ是特征值方程det(A-λI) = 0的多重根。我们需要找到与特征值λ相关的特征向量。 首
搜索技术的很多方面的知识发现都依赖于特征值或奇异值问题，涉及到特征值计算问题。 计算特征值没有直接的方法。 定位特征值的计算方法基于幂迭代的思想，这是求解特征值的一类迭代方法。该思想的一个复杂版本被称为QR算法，是确定典型矩阵所有特征值的一般方法。
