邻接矩阵
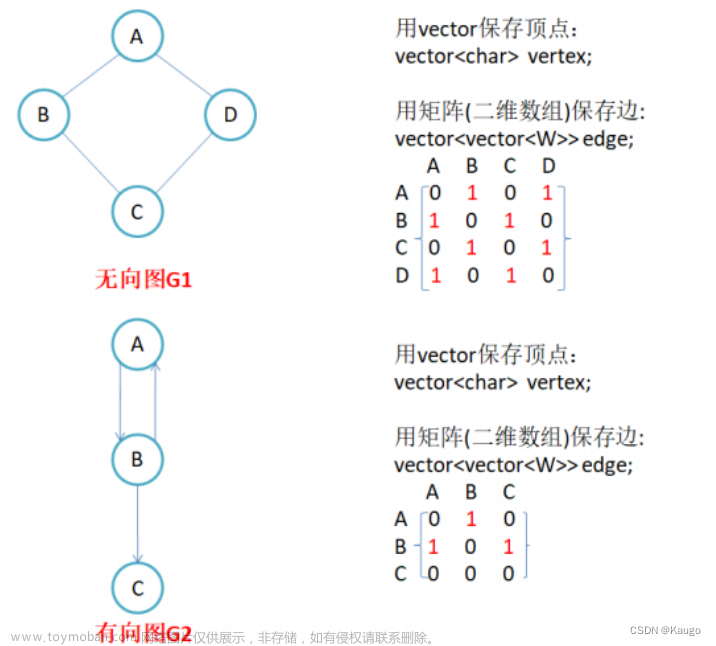
邻接矩阵(Adjacency Matrix)是表示顶点之间相邻关系的矩阵。
设G=(顶点,边):G=(V,E)是一个图。其中V={v1,v2,…,vn} [1] 。G的邻接矩阵是一个具有下列性质的n阶方阵:
- 无向图的邻接矩阵一定是成对角线对称的,是一个对称矩阵,有向图不一定是对称的。
- 有向图当把它的行i固定时,遍历每一列j,得到的是顶点i的出度;当把列j固定时,遍历每一行,得到的是顶点i的入度。


- 对于n个顶点和e条边的邻接矩阵存储时占用的空间是O(n^2),与边数e无关,邻接矩阵适合用于存储稠密图,任何图的邻接矩阵的表示都是唯一,图采用邻接矩阵来描述i,j之间的边很容易。
临界矩阵的结构分为两部分:V和E集合,其中,V是顶点,E是边。
因此,用一个一维数组存放图中所有顶点数据;用一个二维数组存放顶点间关系(边或弧)的数据,这个二维数组称为邻接矩阵。
邻接矩阵又分为有向图邻接矩阵和无向图邻接矩阵
#define INF 0x3F3F3F3F
constexpr auto MAXN = 100;
//存储图中所有顶点的数据:一维数组
struct Vertex
{
int Vid; //顶点编号
string VInfo; //顶点信息
};
//存储图中的顶点与边关系:二维数组
struct Graph
{
int e, n; //e: 实际边数 n:实际定点数
Vertex vers[MAXN]; //顶点集合
int edge[MAXN][MAXN]; //边的集合
}A;
图的邻接矩阵的表示格式:
邻接矩阵
1. 不带权的图的邻接矩阵的表示形式:
{ 1 :对于无向图(i,j)(j,i),对于有向图<i,j>
A[i][j]= 0 :i == j
0 :其他情况
}
2. 带权的图的邻接矩阵的表示形式:
{ w :对于无向图(i,j)(j,i),对于有向图<i,j>
A[i][j]= 0 :i == j
INF :其他情况
}
#include <iostream>
#include <vector>
using namespace std;
#define INF 0x3F3F3F3F
//1.创建邻接矩阵
constexpr auto MAXN = 100;
struct Vertex
{
int Vid; //顶点编号
string VInfo; //顶点信息
};
struct Graph
{
int e, n; //e: 实际边数 n:实际定点数
Vertex vers[MAXN]; //顶点集合
int edge[MAXN][MAXN]; //边的集合
};
class adjacent_matrix
{
public:
adjacent_matrix() {}
~adjacent_matrix() {}
//1. 创建图的邻接矩阵
void CreateGraph(vector<vector<int>>& A, int n, int e)
{
g.e = e;
g.n = n;
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
g.edge[i][j] = A[i][j];
}
}
}
//2.输出图
friend ostream& operator<<(ostream& os, adjacent_matrix lhs)
{
for (int i = 0; i < lhs.g.n; i++)
{
for (int j = 0; j < lhs.g.n; j++)
{
if (lhs.g.edge[i][j] < INF)
{
os << lhs.g.edge[i][j] << " ";
}
else
{
os << "* ";
}
}
os << endl;
}
return os;
}
//3. 求顶点度的运算
// 3.1无向图的顶点度
int Degree1(int v)
{
int d = 0;
if (v < 0 || v >= g.n)
{
return -1;
}
for (int i = 0; i < g.n; i++)
{
if (g.edge[v][i] > 0 && g.edge[v][i] < INF)
{
d++;
}
}
return d;
}
// 3.2有向图的定点度
int Degree2(int v)
{
int d = 0;
if (v < 0 || v >= g.n)
{
return -1;
}
for (int i = 0; i < g.n; i++)
{
if (g.edge[v][i] > 0 && g.edge[v][i] < INF)
{
//行:求出度
d++;
}
}
for (int i = 0; i < g.n; i++)
{
if (g.edge[i][v] > 0 && g.edge[i][v] < INF)
{
//列:求入度
d++;
}
}
return d;
}
public:
Graph g;
};
int main()
{
adjacent_matrix a;
int n = 5, e = 7;
vector<vector<int>> A = {
{0,1,2,6,INF},
{INF,0,INF,4,5},
{INF,INF,0,INF,3},
{INF,INF,INF,0,INF},
{INF,INF,INF,7,0}
};
a.CreateGraph(A, n, e);
cout << a;
cout << "顶点及其度:" << endl;
for (int i = 0; i < n; i++)
{
cout << i << ":--" << a.Degree2(i) << endl;
}
return 0;
}

邻接表
邻接表,是一种链式存储结构,存储方法跟树的孩子链表示法相类似,是一种顺序分配和链式分配相结合的存储结构。如这个表头结点所对应的顶点存在相邻顶点,则把相邻顶点依次存放于表头结点所指向的单向链表中。

在邻接表中:文章来源:https://www.toymoban.com/news/detail-754570.html
- 图中每个顶点建立一个带头节点的单链表,单链表的所有节点由与这个顶点所相邻的所有顶点构成的节点组成。
- 每个顶点构成一条边,称为边节点
- 所有的顶点的单链表构成一个数组,称为头节点数组。
//边节点
struct Node
{
int Neid; //相邻点节点的序号
int weight; //节点权值
Node* next; //指向下一个节点的指针
};
//每个顶点的单链表
struct VexNode
{
string VexInfo; //第一个顶点的信息
Node* head; //单链表的头节点类型
};
//图
struct Graph
{
int n, e; //n:实际顶点数 e:实际边数
VexNode graph[MAXN]; //单链表数组
};
完整代码:文章来源地址https://www.toymoban.com/news/detail-754570.html
#include "change.h"
/*
邻接表:以链式结构存储图的结构
*/
#define MAXN 100
#define INF 0x3F3F3F3F
//边节点
struct Node
{
int Neid; //相邻点节点的序号
int weight; //节点权值
Node* next; //指向下一个节点的指针
};
//每个顶点的单链表
struct VexNode
{
string VexInfo; //第一个顶点的信息
Node* head; //单链表的头节点类型
};
//图
struct Graph
{
int n, e; //n:实际顶点数 e:实际边数
VexNode graph[MAXN]; //单链表数组
};
//邻接表
class AdjGraph
{
public:
AdjGraph()
{
G = nullptr;
}
~AdjGraph() {}
//创建邻接表
void CreateGraph(vector<vector<int>> A, int n, int e)
{
G = new Graph;
G->n = n; G->e = e;
//首先初始化图中全部顶点的单链表为nullptr
for (int i = 0; i < G->n; i++)
{
G->graph[i].head = nullptr;
}
for (int i = 0; i < G->n; i++)
{
//单链表连接的时候从小到大
for (int j = G->n - 1; j >= 0; j--)
{
if (A[i][j] > 0 && A[i][j] < INF)
{
Node* p = new Node;
p->Neid = j;
p->weight = A[i][j];
//单链表头插
p->next = G->graph[i].head;
G->graph[i].head = p;
}
}
}
}
//销毁邻接表
void destroyGraph()
{
for (int i = 0; i < G->n; i++)
{
//遍历图中每一个顶点单链表
Node* temp = nullptr;
Node* cur = G->graph[i].head;
while (cur)
{
temp = cur->next;
memset(cur, NULL, sizeof(cur));
delete cur;
cur = nullptr;
cur = temp;
}
}
}
//输出图
void display()
{
for (int i = 0; i < G->n; i++)
{
//遍历每个顶点单链表
cout << i << ": ";
Node* head = G->graph[i].head;
while (head)
{
cout << "->";
cout << head->Neid << "(" << head->weight << ")";
head = head->next;
}
cout << endl;
}
}
//求顶点的度:无向图的单链表的节点个数就是该节点的度
int Degree1(int v)
{
int d = 0;
auto head = G->graph[v].head;
while (head)
{
d++;
head = head->next;
}
return d;
}
//有向图的顶点的度:出度+入度
int Degree2(int v)
{
int d = 0;
Node* outhead = G->graph[v].head;
//求出度:顶点单链表的节点个数
while (outhead)
{
d++;
outhead = outhead->next;
}
//求入度:每个单链表中是否存在此顶点节点
for (int i=0;i<G->n;i++)
{
Node* cur = G->graph[i].head;
while (cur)
{
if (cur->Neid == v)
{
d++;
break;
}
cur = cur->next;
}
}
return d;
}
public:
Graph* G;
};
//练习1:邻接矩阵转换为邻接表
Graph* change1(matrix lhs)
{
Graph* nG = new Graph;
nG->n = lhs.g.n;
nG->e = lhs.g.e;
for (int i = 0; i < nG->n; i++)
{
nG->graph[i].head = nullptr;
}
for (int i = 0; i < lhs.g.n; i++)
{
//邻接矩阵:行出度,列入度
for (int j = lhs.g.n - 1; j >= 0; j--)
{
//行:出度
if (lhs.g.edge[i][j] > 0 && lhs.g.edge[i][j] < INF)
{
//<i,j>是一个路径
Node* node = new Node;
node->Neid = j;
node->weight = lhs.g.edge[i][j];
//头插
node->next = nG->graph[i].head;
nG->graph[i].head = node;
}
}
}
return nG;
}
//练习1:邻接表转换为邻接矩阵
void change2(matrixGraph &g,Graph* lhs)
{
g.e = lhs->e;
g.n = lhs->n;
for (int i = 0; i < g.n; i++)
{
for (int j = 0; j < g.n; j++)
{
//对角线元素置零,其他元素置INF
if (i == j) g.edge[i][j] = 0;
else g.edge[i][j] = INF;
}
}
for (int i = 0; i < lhs->n; i++)
{
//顶点出度:遍历每一个顶点单链表的节点
Node* cur = lhs->graph[i].head;
while (cur)
{
// i->j
g.edge[i][cur->Neid] = cur->weight;
cur = cur->next;
}
}
}
int main()
{
AdjGraph Ga;
int n = 5, e = 7;
vector<vector<int>> A = {
{0,1,2,6,INF},
{INF,0,INF,4,5},
{INF,INF,0,INF,3},
{INF,INF,INF,0,INF},
{INF,INF,INF,7,0}
};
Ga.CreateGraph(A, n, e);
Ga.display();
cout << "顶点及其度:" << endl;
for (int i = 0; i < n; i++)
{
cout << i << ":--" << Ga.Degree2(i) << endl;
}
matrix ga;
ga.CreateGraph(A, n, e);
cout << ga;
cout << "顶点及其度:" << endl;
for (int i = 0; i < n; i++)
{
cout << i << ":--" << ga.Degree2(i) << endl;
}
//邻接矩阵转化为邻接表
auto Gp = change1(ga);
//邻接表转换为邻接矩阵
matrixGraph g;
change2(g,Gp);
return 0;
}
到了这里,关于图论基础: 邻接矩阵与邻接表(c++实现)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!